Giải bởi Vietjack
Lời giải
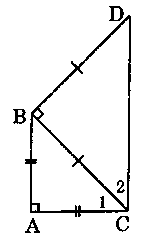
Vì ∆ABC vuông cân tại A nên \(\widehat {ABC} = \widehat {{C_1}}\)
Lại có: \(\widehat {ABC} + \widehat {{C_1}} = 90^\circ \) (tính chất tam giác vuông).
Suy ra: \[\widehat {{C_1}} = 45^\circ \]
Vì ∆BCD vuông cân tại B nên \(\widehat D = \widehat {{C_2}}\)
Lại có: \(\widehat D + \widehat {{C_2}} = 90^\circ \)(tính chất tam giác vuông).
Suy ra: \[\widehat {{C_2}} = 45^\circ \]
\(\widehat {ACD} = \widehat {{C_1}} + \widehat {{C_2}} = 45^\circ + 45^\circ = 90^\circ \)
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB // CD
Vậy tứ giác ABCD là hình thang vuông.
Cho đường tròn (O), đường kính AB cố định, M là 1 điểm thuộc (O), (M khác A và B). Các tiếp tuyến của (O) tại A và M cắt nhau ở C. Đường tròn (I) đi qua M và tiếp xúc với đường thẳng AC tại C, CD là đường kính của (I). Chứng minh rằng:
a) 3 điểm O, M, D thẳng hàng.
b) Tam giác COD là tam giác cân.
c) Gọi N là giao điểm của OC và (I). Chứng minh khi M thay đổi thì đường thẳng qua N vuông góc với AB luôn đi qua điểm cố định.
Cho tam giác ABC nhọn. Gọi M và N lần lượt là trung điểm của AB, BC.
a) Tính độ dài của MN biết AC = 16cm.
b) Gọi I là trung điểm của AC. Chứng minh tứ giác BMIN là hình bình hành.
c) Trên tia đối của tia NM lấy E sao cho N là trung điểm ME. Gọi K là giao điểm của EI và MC. Chứng minh MC = 3KC.
Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ 2 tiếp tuyến AM, AN với đường tròn (O). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:
a, 5 điểm A, O, M, N, F cùng nằm trên 1 đường tròn.
b, 3 điểm M, N, H thẳng hàng.
c, HA . HF = R2 – OH2.
Tìm giá trị của x để đa thức dư trong mỗi phép chia sau có giá trị bằng 0:
a) (3x5 – x4 – 2x3 + x2 + 4x + 5) : (x2 – 2x + 2);
b) (x5 + 2x4 + 3x2 + x – 3) : (x2 + 1).
