Cho nửa đường tròn đường kính AB, dây CD. Gọi H, K theo thứ tự là chân các đường vuông góc kẻ từ A, B đến CD
a) Chứng minh rằng: CH = DK
b) Chứng minh rằng: SAHKB = SACB + SADB
c) Tính diện tích lớn nhất của tứ giác AHKB, biết AB = 30 cm, CD = 18 cm
Giải bởi Vietjack
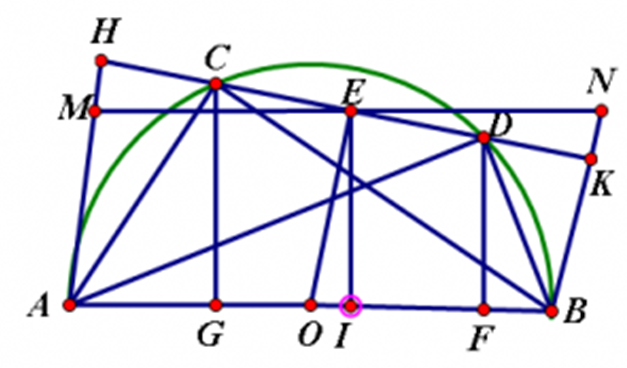
a) Gọi O là tâm đường tròn đường kính AB
Kẻ OE vuông góc với CD (E thuộc CD)
Suy ra E là trung điểm của CD
Mà OE là đường trung bình của hình thang ABKH (đi qua trung điểm một cạnh bên và song song với cạnh đáy)
Þ EH = EK mà EC = ED
Suy ra CH = DK (đpcm)
b) Hạ CG, DF ^ AB tại G, F
Þ CG // DF
Þ Tứ giác CDGF là hình thang.
Lấy I là trung điểm của GF.
Xét hình thang CDGF có:
EC = ED (E là trung điểm của CD)
IG = IF (I là trung điểm của GF)
Þ EI là đường trung bình của hình thang CDFG
\( \Rightarrow EI = \frac{{DF + CG}}{2}\)
Ta có: \[{S_{ACB}} + {S_{ADB}} = \frac{{AB + CG}}{2} + \frac{{AB + DF}}{2} = AB\,.\,\frac{{CG + DF}}{2} = AB\,.\,EI\] (1)
Qua E kẻ đường thẳng song song với AB cắt AH, BK lần lượt ở M, N.
Dễ thấy tứ giác AMNB là hình bình hành (vì có 2 cặp cạnh đối song song )
Þ SAMNB = AB.EI
Xét ∆MHE và ∆NKE có:
\(\widehat {MEH} = \widehat {NEK}\) (2 góc đối đỉnh)
\(\widehat {MHE} = \widehat {NKE} = 90^\circ \)
EM = EN
Do đó ∆HEM = ∆KEN (cạnh huyền – góc nhọn)
Þ SHEM = SKEN
Khi đó:
SAHKB = SAMEKB + SMHE = SAMEKB + SENK = SAMNB = AB.EI (2)
Từ (1) và (2) Þ SAHKB = SACB + SADB
c) \({S_{AHKB}} = \frac{{\left( {AH + BK} \right)\,.\,HK}}{2} = \frac{{2OE\,.\,HK}}{2} = OE\,.\,HK\)
\(OE = \sqrt {O{D^2} - E{D^2}} = \sqrt {{{15}^2} - {9^2}} = 12\)
Þ S = 12.HK ≤ 12.AB = 12.30 = 360
Þ Smax = 360.
Rút gọn biểu thức: cos2 10° + cos2 20° + cos2 30° + ... + cos2 180°.
Cho tam giác ABC có \(\widehat {ABC} = 30^\circ \), AB = 5, BC = 8. Tính \[\overrightarrow {BA} \,.\,\overrightarrow {BC} \].
Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên AB và AC
a) Chứng minh AM.AB = AN.AC.
b) Chứng minh tam giác AMN đồng dạng tam giác ACB.
Cho hình vuông ABCD có AC cắt BD tại O. M là điểm bất kỳ thuộc cạnh BC (M khác B, C). Tia AM cắt đường thẳng CD tại N. Trên cạnh AB lấy điểm E sao cho BE = CM.
a) Chứng minh: ∆OEM vuông cân.
b) Chứng minh: ME // BN.
c) Từ C kẻ CH vuông góc BN (H thuộc BN). Chứng minh rằng ba điểm O, M, H thẳng hàng.
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân.
Cho hình vuông ABCD có AC cắt BD tại O. Gọi E và F theo thứ tự là các điểm đối xứng với O qua AD và BC .
a) Chứng minh rằng các tứ giác AODE, BOCF là hình vuông
b) Nối EC cắt DF tại I. Chứng minh rằng OI ^ CD
c) Biết diện tích hình lục giác ABFCDE = 6. Tính độ dài các cạnh của hình vuông ABCD
d) Lấy K là 1 điểm bất kì trên BC. Gọi G là trọng tâm của tam giác AIK. Chứng minh G thuộc 1 đường thẳng cố định khi K di chuyển trên BC
Cho nửa đường tròn tâm O đường kính AB, M là một điểm bất kỳ thuộc nửa đường tròn (M khác A, B). Tiếp tuyến tại M cắt các tiếp tuyến Ax và By của nửa đường tròn đó lần lượt tại C và D. Gọi K là giao điểm của BM với Ax. Tìm giá trị nhỏ nhất của tổng diện tích hai tam giác ACM và BDM.
Cho hình chữ nhật ABCD. Gọi E là điểm đối xứng của B và C.
a) Chứng minh tứ giác ACED là hình bình hành.
b) Gọi M là trung điểm của BC. Tia AM cắt tia DC tại F. Chứng minh tứ giác BDEF là hình thoi.
c) Gọi I là giao điểm của AE và DC. Tia BI cắt tia DE tại . Chứng minh \(KI = \frac{1}{6}AE.\)
Cho hình chữ nhật ABCD. Vẽ điểm E đối xứng với B qua điểm C; vẽ F đối xứng với điểm D qua C.
a) Chứng minh tứ giác BDEF là hình thoi.
b) Chứng minh AC = DE.
c) Gọi H là trung điểm của CD, K là trung điểm của EF. Chứng minh HK // AC.
d) Biết diện tích tam giác AEF bằng 30 cm2. Tính diện tích hình chữ nhật ABCD.Cho x + y + z = 0. Rút gọn: \(A = \frac{{{x^2} + {y^2} + {z^2}}}{{{{\left( {x - y} \right)}^2} + {{\left( {y - z} \right)}^2} + {{\left( {z - x} \right)}^2}}}\).
Cho tam giác ABC đều cạnh a. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AI} } \right|\), I là trung điểm BC.
Cho hình vuông ABCD có cạnh bằng a. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. M là giao điểm của CE và DF.
a) Chứng minh tứ giác EFGH là hình vuông.
b) Chứng minh DF ^ CE và ∆MAD cân.
c) Tính diện tích tam giác MDC theo a.
Cho tam giác nhọn ABC, \(\widehat B > \widehat C\). Gọi H là hình chiếu của A trên BC. Sắp xếp các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần.
Gọi S là tập hợp các số tự nhiên có 6 chữ số. Chọn ngẫu nhiên một số từ S, tính xác suất để các chữ số của số đó đôi một khác nhau và phải có mặt chữ số 0 và 1.
