Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB // CD và AB = 2DC. Gọi O là giao điểm của AC và BD, G là trọng tâm tam giác SBC, H là giao điểm của DG và (SAC). Tính tỉ số \[\frac{{GH}}{{GD}}\].
Giải bởi Vietjack
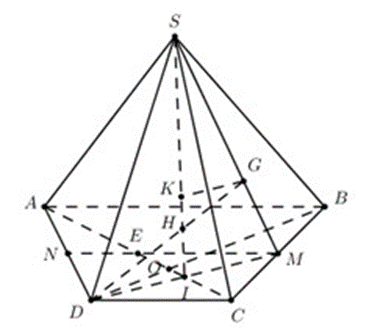
Gọi M là trung điểm của BC, I = AC ∩ DM .
Trong (SDM) gọi H = DG ∩ SI ta có:
• I ∈ AC ⇒ I ∈ (SAC) ⇒ SI ⊂ SAC
• H ∈ SI ⇒ H ∈ (SAC) ⇒ H = DG ∩ (SAC).
Gọi N là trung điểm của AD, E = AC ∩ MN
Nên MN là đường trung bình của hình thang ABCD
\[ \Rightarrow MN = \frac{{AB + CD}}{2} = \frac{{2CD + CD}}{2} = \frac{{3CD}}{2}\]
Áp dụng định lí Ta-lét, ta có:
• \[\frac{{NE}}{{CD}} = \frac{{AN}}{{AD}} = \frac{1}{2} \Rightarrow NE = \frac{1}{2}CD \Rightarrow ME = \frac{3}{2}CD - \frac{1}{2}CD = CD\]
• \[\frac{{IM}}{{ID}} = \frac{{CD}}{{MN}} = \frac{{ME}}{{CD}} = 1 \Rightarrow IM = ID\]
Kẻ GK // DM, áp dụng định lí Vi-ét ta có:
\[\frac{{GH}}{{DH}} = \frac{{KG}}{{ID}} = \frac{{KG}}{{IM}} = \frac{{KG}}{{IM}} = \frac{{SG}}{{SM}} = \frac{2}{3}\]
\[ \Rightarrow \frac{{GH}}{{GH + DH}} = \frac{2}{{2 + 3}} = \frac{2}{5} \Rightarrow \frac{{GH}}{{GD}} = \frac{2}{5}\].
Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H. QE cắt DC tại M. Gọi N là hình chiếu của E trên AD, MN cắt DE tại O. Chứng minh tam giác OEM là tam giác cân.
Hỏi có bao nhiêu giá trị m nguyên trong [−2017;2017] để phương trình:
log(mx) = 2log(x + 1) có nghiệm duy nhất?
Cho hàm số f(x) thỏa mãn \[f\left( 2 \right) = - \frac{2}{9}\]và f ′(x) = 2x[f(x)]2 với mọi \[x \in \mathbb{R}\]. Tính giá trị của f(1).
Cho hình nón (N) có bán kính đáy bằng 4, diện tích xung quanh bằng 20π. Tính thể tích khối nón đã cho.
Một trong các bạn A, B, C và D làm vỡ kính cửa sổ. Khi được hỏi, họ trả lời như sau:
A: “C làm vỡ”.
B: “Không phải tôi”.
C: “D làm vỡ”.
D: “C đã nói dối”.
Nếu có đúng một người nói thật thì ai đã làm vỡ cửa số.
Tích tất cả các nghiệm của phương trình \[\log _3^2x - 2{\log _3}x - 7 = 0\] là?
Cho tam giác ABC, có bao nhiêu điểm M thỏa mãn: \[\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = 3?\]
Tìm m để phương trình: x2 + mx – 2 = 0 có 2 nghiệm phân biệt x1, x2 cùng nhỏ hơn 1.
Có bao giá trị nguyên của tham số m để phương trình:
4x – m.2x + 1 + 2m2 – 5 = 0 có hai nghiệm phân biệt?
Tổng tất cả các giá trị nguyên của tham số m để đồ thị hàm số:
y = ∣3x4 + 8x3 − 6x2 − 24x − m∣ có 7 điểm cực trị.
Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng \[\frac{{{a^3}}}{6}\]. Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.
Chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.
Cho x, y thỏa mãn x – 2y + 2 = 0. Tìm giá trị nhỏ nhất của biểu thức:
\[T = \sqrt {{{(x - 3)}^2} + {{(y - 5)}^2}} + \sqrt {{{(x - 5)}^2} + {{(y - 7)}^2}} \].
