Cho khối trụ có chiều cao h = 8, bán kính đường tròn đáy bằng 6, cắt khối trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 4. Tính diện tích thiết diện tạo thành.
Giải bởi Vietjack
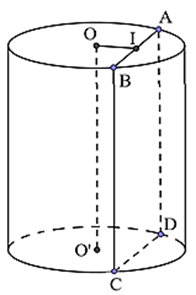
Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 4 < R (R = 6).
Suy ra thiết diện là hình chữ nhật.
Giả sử thiết diện là hình chữ nhật ABCD (như hình vẽ), gọi I là trung điểm của AB.
Theo đề bài ta có:
OI = d(OO'; (ABCD)) = 4, BC = h = 8, R = 6
Tam giác OIA vuông tại I
\( \Rightarrow IA = \sqrt {O{A^2} - O{I^2}} = \sqrt {{6^2} - {4^2}} = 2\sqrt 5 \).
Diện tích của thiết diện là:
\({S_{ABCD}} = AB\,.\,BC = 4\sqrt 5 \,.\,8 = 32\sqrt 5 \).
Giải phương trình sau: \({7^x}\,.\,{27^{\left( {1\, - \,\frac{1}{x}} \right)}} = 3087\).
Tính tổng các nghiệm thuộc khoảng \(\left( { - \frac{\pi }{2};\;\frac{\pi }{2}} \right)\) của phương trình
4sin2 2x − 1 = 0.
Có bao nhiêu giá trị m nguyên thuộc khoảng (−10; 10) để đồ thị hàm số \(y = \frac{{\sqrt {x\left( {x - m} \right)} - 1}}{{x + 2}}\) có đúng ba đường tiệm cận?
Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R. Khi đó bán kính R bằng bao nhiêu?
Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị là A(1; −7); B(2; −8). Tính y (−1).
Tìm tất cả giá trị thực của tham số m để phương trình cos 2x − (2m + 1)cos x + m + 1 = 0 có nghiệm trên khoảng \(\left( {\frac{\pi }{2};\;\frac{{3\pi }}{2}} \right)\).
Ông A dự định sử dụng hết 5m2 kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Cho x, y là các số thực không âm thỏa mãn: x2 − 2xy + x − 2y ≤ 0.
Tìm GTLN của M = x2 − 5y2 + 3x.
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d Î ℝ) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
Cho khối trụ có hai đáy là (O) và (O'). AB, CD lần lượt là hai đường kính của (O) và (O'), góc giữa AB và CD bằng 30°, AB = 6 và thể tích khối tứ diện ABCD bằng 30. Thể tích khối trụ đã cho bằng:
Tìm hệ số của số hạng chứa x10 trong khai triển của biểu thức \({\left( {3{x^3} - \frac{2}{{{x^2}}}} \right)^5}\)
