Cho hình chóp S.ABC có SA ^ (ABC). AB = a; \(AC = a\sqrt 2 ;\;\widehat {BAC} = 45^\circ \). Gọi B1, C1 lần lượt là hình chiều vuông góc của A lên SB, SC. Tính thể tích mặt cầu ngoại tiếp hình chóp A.BCC1B1.
Giải bởi Vietjack
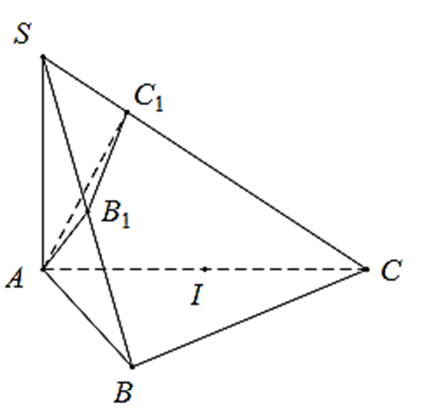
Tam giác ABC có AB = a; \(AC = a\sqrt 2 ;\;\widehat {BAC} = 45^\circ \) nên theo định lý cosin ta có:
BC2 = AB2 + AC2 − 2AB.AC.cos 45° = a2
Þ BC = a
Suy ra ∆ABC vuông cân tại B
Gọi I là trung điểm AC, ta có IA = IC = IB
Vì AC1 ^ SC nên IA = IC = IC1
Vì BC ^ SA, BC ^ AB
Þ BC ^ (SAB) Þ BC ^ AB1
Mà AB1 ^ SB Þ AB1 ^ (SBC)
Þ AB1 ^ B1C
Þ IA = IC = IB1
Vậy I là tâm mặt cầu ngoại tiếp chóp A.BCC1B1.
Bán kính của khối cầu đó là: \(R = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\).
Thể tích khối cầu đó là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\frac{{a\sqrt 2 }}{2}} \right)^3} = \frac{{\pi {a^3}\sqrt 2 }}{3}\).
Cho hàm số: y = 3 − 5sin x, giá trị lớn nhất và nhỏ nhất của hàm số là M và m. Tính \(\frac{M}{m}\).
Cho y = 2x + m + 1. Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2.
Tìm m để y = x3 − 3x2 + mx − 1 có hai điểm cực trị x1, x2 thỏa mãn x12 + x22 = 3.
Cho hai đường thẳng song song d1 và d2. Trên d1 lấy 17 điểm phân biệt, trên d2 lấy 20 điểm phân biệt. Tính số tam giác mà có các đỉnh được chọn từ 37 điểm này.
Cho tam giác ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H. Đường thẳng EF cắt đường tròn (O) tại M, N (F nằm giữa M và E). Chứng minh rằng: .
Cho hình chóp tam giác S.ABC với SA, SB, SC đôi một vuông góc và SA = SB = SC = a. Tính thể tích của khối chóp S.ABC.
Tìm GTLN và GTNN của hàm số sau: \(y = 1 - \sqrt {2{{\cos }^2}x + 1} \).
Cho đường tròn (O; R). Có bao nhiêu phép vị tự biến (O; R) thành chính nó?
Tìm tất cả các giá trị của tham số m để hàm số y = −x3 + 3x2 + mx + 1 nghịch biến trên khoảng (0; +∞).
Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A, AB = 2a, \(\widehat {BAC} = 120^\circ ,\;\widehat {SBA} = \widehat {SCA} = 90^\circ \). Biết góc giữa SB và đáy bằng 60°. Tính thể tích V của khối chóp S.ABC.
Cho hình lập phương ABCD có cạnh là 2. Gọi M, N lần lượt là trung điểm của BC và CD. Tính diện tích thiết diện của hình lập phương khi cắt bởi mặt phẳng (A'MN).
Có bao nhiêu giá trị nguyên của m để phương trình 22x + 1 − 2x + 3 − 2m = 0 có hai nghiệm phân biệt?
Cho ba điểm A(2; 2), B(3; 5), C(5; 5). Tìm tọa độ điểm D sao cho ABCD là một hình bình hành.
Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H (D Î BC, E Î AC, F Î AB). Chứng minh các tứ giác BDHF, BFEC nội tiếp.
