Cho đường tròn tâm O bán kính 3 cm. Từ một điểm A cách O là 5 cm vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm).
a) Chứng minh AO vuông góc với BC
b) Kẻ đường kính BD. Chứng minh rằng DC song song với OA
c) Tính chu vi và diện tích tam giác ABC.
d) Qua O kẻ đường thẳng vuông góc với BD, đường thẳng này cắt tia DC tại E. Đường thẳng AE và OC cắt nhau ở I; đường thẳng OE và AC cắt nhau ở G. Chứng minh IG là trung trực của đoạn thẳng OA.
Giải bởi Vietjack
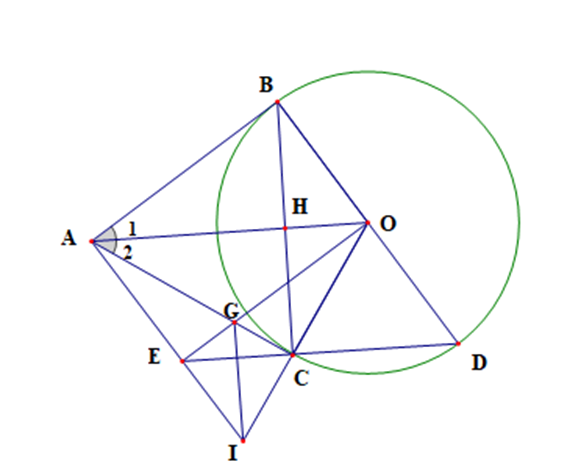
a) Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A nên AB = AC và AO là tia phân giác của \(\widehat {BAC}\)
Do đó ∆ABC cân tại A có AO là phân giác đồng thời là đường cao, hay AO ⊥ BC.
b) Vì ∆BCD nội tiếp đường tròn (O) nên ∆BCD vuông tại C
Do đó CD ⊥ BC
Mà AO ⊥ BC nên CD // AO.
c) Vì ∆AOB vuông tại B nên theo định lý Pythagore có:
\[AB = \sqrt {A{O^2} - B{O^2}} = \sqrt {{5^2} - {3^2}} = 4\]
Gọi H là giao điểm của AO và BC.
Áp dụng hệ thức lượng trong tam giác vuông ABO có:
⦁ AB2 = AH . AO \( \Rightarrow AH = \frac{{A{B^2}}}{{AO}} = \frac{{16}}{5} = 3,2\)
⦁ \(\frac{1}{{B{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{B{O^2}}} \Leftrightarrow \frac{1}{{B{H^2}}} = \frac{1}{{{4^2}}} + \frac{1}{{{3^2}}}\). Suy ra BH = 2,4
Do đó BC = 2AH = 2 . 2,4 = 4,8
Chu vi tam giác ABC là: AB + AC + BC = 4 + 4 + 4,8 = 12,8 (cm).
Diện tích tam giác ABC là \({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}.3,2.4,8 = 7,68\) (cm2).
d) Vì AO // CD nên \(\widehat {BOA} = \widehat {O{\rm{D}}E}\) (hai góc đồng vị)
Xét ∆ABO và ∆EOD có
\(\widehat {ABO} = \widehat {EO{\rm{D}}}\left( { = 90^\circ } \right)\);
BO = DO;
\(\widehat {BOA} = \widehat {O{\rm{D}}E}\) (chứng minh trên)
Suy ra ∆ABO = ∆EOD (g.c.g)
Do đó AB = EO (hai cạnh tương ứng)
Mà AB // EO (vì cùng vuông góc với BD)
Nên ABOE là hình bình hành
Lại có \(\widehat {AOB} = 90^\circ \) nên hình bình hành ABOE là hình chữ nhật.
Suy ra \(\widehat {A{\rm{E}}O} = 90^\circ \) hay OE ⊥ AI
Xét tam giác AIO có hai đường cao OE và AC cắt nhau tại G
Suy ra G là trực tâm, nên OA ⊥ GI
Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A nên OA là tia phân giác của \(\widehat {BOC}\)
Do đó \(\widehat {I{\rm{O}}A} = \widehat {BOA}\)
Mà \(\widehat {O{\rm{D}}E} = \widehat {BOA}\) suy ra \(\widehat {I{\rm{O}}A} = \widehat {ODE}\) (1)
Ta có EO ⊥ AI, EO ⊥ OD suy ra AE // OD
Mà AO // ED nên AODE là hình bình hành
Suy ra \(\widehat {O{\rm{D}}E} = \widehat {OA{\rm{E}}}\) (2)
Từ (1) và (2) suy ra \(\widehat {I{\rm{O}}A} = \widehat {OAE}\)
Do đó tam giác AOI cân tại I
Lại có IG là đường cao
Suy ra IG là đường trung trực của AO
Vậy IG là đường trung trực của AO.
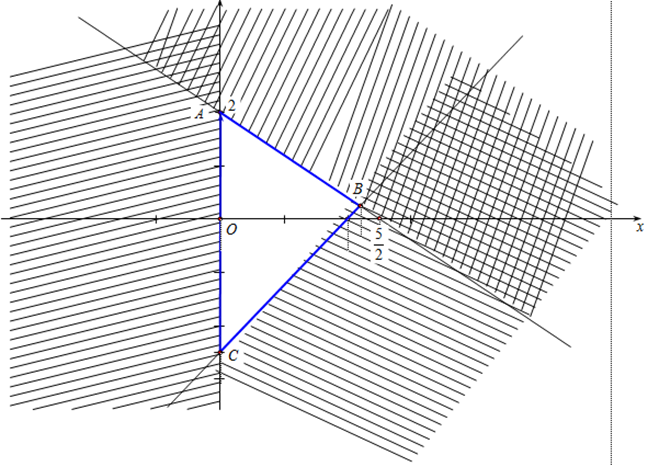
Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn bệ A, B, C, D?
Một người chọn ngẫu nhiên hai chiếc giày từ bốn đôi giày cỡ khác nhau. Tính xác suất để hai chiếc chọn được tạo thành một đôi.
Trong mặt phẳng Oxy cho \(\overrightarrow a \left( {1;3} \right)\) và \(\overrightarrow b \left( { - 2;1} \right)\). Tích vô hướng \(\overrightarrow a .\overrightarrow b \) là:
Trong mặt phẳng Oxy cho điểm M(1; 1). Điểm nào sau đây là ảnh của M qua phép quay tâm O, góc quay 45°.
Cho đường tròn (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC vuông góc với OA. Biết độ dài đường tròn (O) là 4π (cm). Độ dài cung lớn BC là:
Có ba chiếc hộp, mỗi chiếc hộp chứa ba chiếc thẻ được đánh số 1, 2, 3. Từ mỗi hộp rút ngẫu nhiên một chiếc thẻ. Xác suất để ba cái thẻ được rút ra có tổng bẳng 6 là?
Gọi S là tập hợp các số tự nhiên có hai chữ số. Trong các số: 7; 15; 106; 99, số nào thuộc và số nào không thuộc tập S? Dùng kí hiệu để trả lời.
Đỉnh của parabol y = x2 + x + m nằm trên đường thẳng \(y = \frac{3}{4}\) nếu m bằng:
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – y + 2 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép quay tâm O góc quay –90°.
Tính thể tích khối chóp tam giác đều có độ dài cạnh bên bằng \(a\sqrt 2 \) và độ dài cạnh đáy bằng a.
Một nhà khoa học nghiên cứu về tác động phối hợp của vitamin A và vitamin B đối với cơ thể con người. Kết quả như sau:
− Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B.
− Một người mỗi ngày cần từ 400 đến 1 000 đơn vị vitamin cả A và B.
Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn \(\frac{1}{2}\) số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A. Biết giá một đơn vị vitamin A là 9 đồng và giá một đơn vị vitamin B là 7,5 đồng. Phương án dùng hai loại vitamin A, B thoả mãn các điều kiện trên để có số tiền phải trả là ít nhất là:
Rút gọn \[{\rm{A}} = \frac{{\sqrt {\sqrt 7 - \sqrt 3 } - \sqrt {\sqrt 7 + \sqrt 3 } }}{{\sqrt {\sqrt 7 - 2} }}\].
Cho hai tập hợp A = (m – 1; 5) và B = (3; +∞). Tìm tất cả các giá trị thực của tham số m để A\B = ∅.
Cho khối chóp S.ABC có các góc phẳng ở đỉnh S bằng 60°, SA = 1, SB = 2, SC = 3. Thể tích của khối chóp S.ABC bằng:
