Cho tam giác MNP có MP = 2MN, MO là phân giác góc NMP. Xét các khẳng định sau:
(I)
Số khẳng định đúng là
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
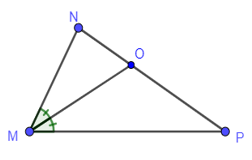
Ta có MP = 2MN, suy ra .
Tam giác MNP có MO là đường phân giác góc M.
Do đó ta có: hay . Vậy (I) đúng.
Suy ra . Vậy (IV) sai.
Vì NO + OP = NP nên NO + 2NO = NP hay 3NO = NP
Suy ra và . Vậy (II) sai, (III) đúng.
Vậy có 2 khẳng định đúng.
Cho tam giác ABC có ba đường phân giác AD, BE, CF cắt nhau tại I. Gọi G, H, K lần lượt là hình chiếu của I lên AB, AC, BC. Biết GI = 12 cm. Độ dài IK là:
Cho tam giác OMN có OD là đường phân giác góc MON (D ∈ MN). Biết DN = 7 cm, ON = 9 cm. Tỉ số là:
Cho tam giác DEF có DI là đường phân giác của góc EDF (I ∈ EF). Biết DE = 5 cm, EF = 9 cm, DF = 8 cm. Tỉ số diện tích của hai tam giác DEI và DFI là:
Cho tam giác ABC có chu vi là 18 cm, các đường phân giác BD, CE. Tính các cạnh của tam giác ABC biết .
Cho tam giác ABC có CE là đường phân giác góc ACB (E ∈ AB). Biết AB = 8 cm, AC = 6 cm, BC = 10 cm, AE = x cm, EB = y cm. Giá trị của x và y lần lượt là:
Cho tam giác ABC cân tại A, AB = AC = m, BC = n. Đường phân giác góc B cắt AC tại I, đường phân giác góc C cắt AB tại H. Khẳng định nào sau đây là đúng?
Cho tam giác ABC có BE là phân giác góc ABC (E ∈ AC). Cho AB = 6 cm, BC = x cm, AE = 5 cm, EC = 3 cm. Giá trị của x là: