Cho điểm A không nằm trên d, kẻ tại H, B và C là các điểm tuỳ ý nằm trên d và khác H. Xét các khẳng định sau:
(I) AH < AB và AH < AC
(II) HB < HC
A. Chỉ có (I) đúng;
B. Chỉ có (II) đúng;
C. Cả (I) và (II) đều đúng;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A
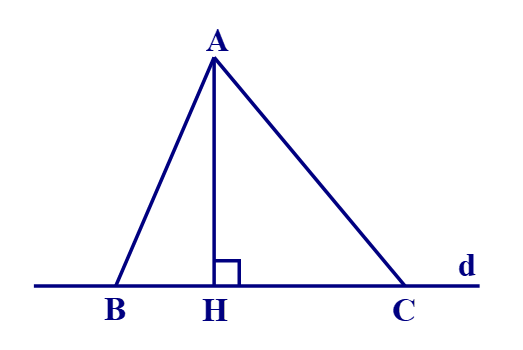
+) Vì tam giác AHB vuông nên AH < AB.
+) Vì tam giác ACH vuông nên AH < AC.
Þ Khẳng định (I) đúng.
+) Áp dụng định lí Pythagore vào tam giác vuông AHB và AHC ta được:
AB2 = AH2 + BH2
AC2 = AH2 + CH2
Nếu AB2 < AC2 thì AB < AC. Suy ra, BH < CH.
Nếu AB2 > AC2 thì AB > AC. Suy ra, BH > CH.
Do đó, BH < CH hoặc BH > CH.
Þ Khẳng định (II) sai.
Cho ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm H.
Khẳng định nào sau đây là đúng?
Cho tam giác ABC có độ dài các cạnh AB, BC, CA lần lượt là 4 cm, 3 cm, 5 cm. Trên tia đối của tia BA lấy điểm M sao cho BM = 2 cm, tại M kẻ đường thẳng vuông góc với AB cắt AC tại H. Khẳng định nào sau đây là đúng?
Cho tam giác ABC có độ dài các cạnh AB, BC, CA lần lượt là 4 cm, 3 cm, 5 cm. Trên tia đối của tia BA lấy điểm M sao cho BM = 2 cm, tại M kẻ đường thẳng vuông góc với AB cắt AC tại H. Chọn khẳng định đúng.