10 câu hỏi trắc nghiệm thuộc Dạng 3. Chứng minh các tính chất hình học

Câu 1:

Nhận xét nào sau đây là đúng?

A. Trong tam giác vuông, cạnh huyền là cạnh lớn nhất;

B. Trong tam giác vuông, cạnh huyền là cạnh bé nhất;

C. Trong tam giác vuông, cạnh góc vuông bằng cạnh huyền;

D. Trong tam giác vuông, cạnh góc vuông lớn hơn cạnh huyền.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Vẽ tam giác ABC vuông tại A.

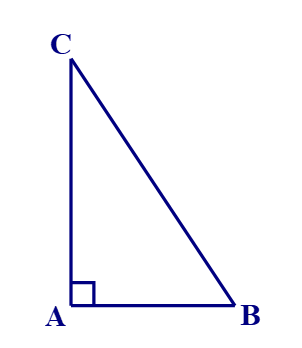
Nhận xét nào sau đây là đúng? A. Trong tam giác vuông, cạnh huyền là cạnh lớn nhất; (ảnh 1)

Áp dụng định lí Pythagore vào tam giác vuông ABC ta được:

BC² = AC² + AB²

Þ AC < BC, AB < BC

Mà BC là cạnh huyền và AB, AC là các cạnh góc vuông.

Vậy trong giác vuông cạnh huyền là cạnh lớn nhất.

Câu 2:

Cho hình vẽ:

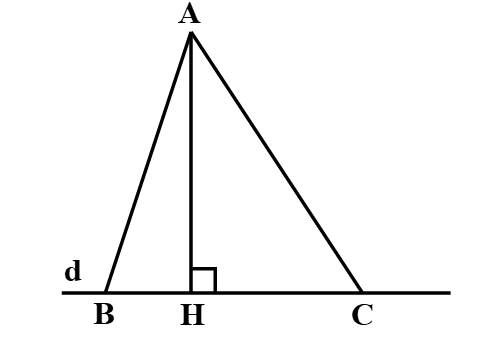
Khẳng định nào sau đây là đúng?

A. HB > HC thì AB > AC;

B. HB > HC thì AB = AC;

C. HB < HC thì AB > AC;

D. HB = HC thì AB > AC.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Áp dụng định lí Pythagore trong tam giác vuông AHB và AHC ta có:

AB² = AH² + BH²

AC² = AH² + CH²

+) Nếu BH < CH thì AB < AC.

+) Nếu BH > CH thì AB > AC.

Vậy khẳng định đúng là HB > HC thì AB > AC.

Câu 3:

Cho ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm H.

Khẳng định nào sau đây là đúng?

A. AH < BH;

B. AH < AB;

C. AH > BH;

D. AH = BH.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

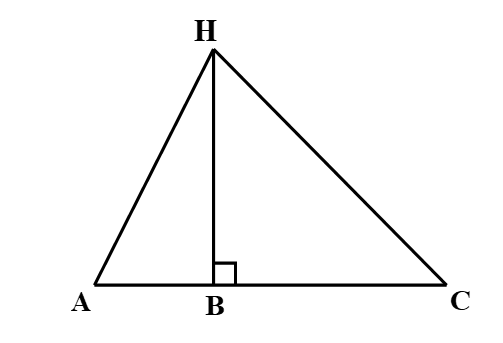
Cho ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm H. (ảnh 1)

Áp dụng định lí Pythagore vào tam giác HBA vuông ở B ta có:

AH² = BH² + AB²

Þ AH > AB, AH > BH.

Câu 4:

Cho hình vẽ sau

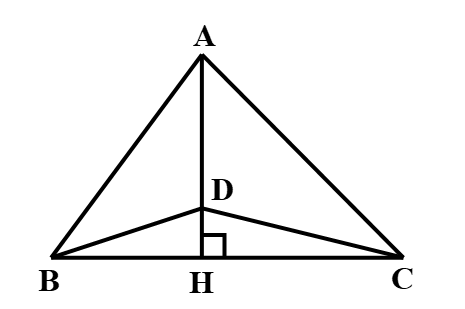
Có AB < AC, khẳng định nào sau đây là đúng?

A. Nếu HB < HC thì BD > DC;

B. Nếu HB < HC thì BD < DC;

C. Nếu HB = HC thì BD < DC;

D. Nếu HB < HC thì BD = DC.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

*) Áp dụng định lí Pythagore vào tam giác vuông AHB và AHC ta có:

AB² = AH² + BH²

AC² = AH² + CH²

Vì AB < AC nên BH < CH.

*) Áp dụng định lí Pythagore vào tam giác vuông BHD và BHC ta có:

BD² = BH² + DH²

CD² = CH² + DH²

Vì BH < CH nên BD < CD.

Câu 5:

Cho điểm A không nằm trên d, kẻ $A H ⊥ d$ tại H, B và C là các điểm tuỳ ý nằm trên d và khác H. Xét các khẳng định sau:

(I) AH < AB và AH < AC

(II) HB < HC

A. Chỉ có (I) đúng;

B. Chỉ có (II) đúng;

C. Cả (I) và (II) đều đúng;

D. Cả (I) và (II) đều sai.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

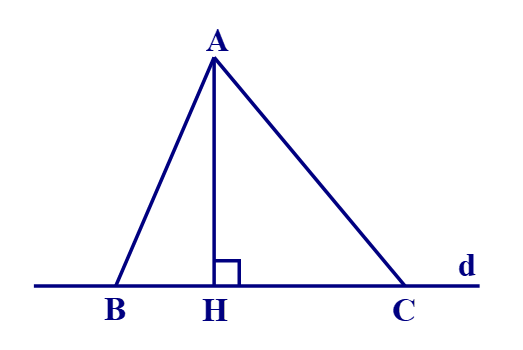
Cho điểm A không nằm trên d, kẻ AH vuông góc d tại H, B và C là các điểm tuỳ ý nằm trên d và khác H. Xét các khẳng định sau: (ảnh 1)

+) Vì tam giác AHB vuông nên AH < AB.

+) Vì tam giác ACH vuông nên AH < AC.

Þ Khẳng định (I) đúng.

+) Áp dụng định lí Pythagore vào tam giác vuông AHB và AHC ta được:

AB² = AH² + BH²

AC² = AH² + CH²

Nếu AB² < AC² thì AB < AC. Suy ra, BH < CH.

Nếu AB² > AC² thì AB > AC. Suy ra, BH > CH.

Do đó, BH < CH hoặc BH > CH.

Þ Khẳng định (II) sai.

Câu 6:

Cho tam giác ABC có độ dài các cạnh AB, BC, CA lần lượt là 4 cm, 3 cm, 5 cm. Trên tia đối của tia BA lấy điểm M sao cho BM = 2 cm, tại M kẻ đường thẳng vuông góc với AB cắt AC tại H. Chọn khẳng định đúng.

A. BC vuông góc MH;

B. BC trùng với MH;

C. BC song song với MH;

D. Tất cả đều sai.

Xem đáp án

Hướng dẫn giải:

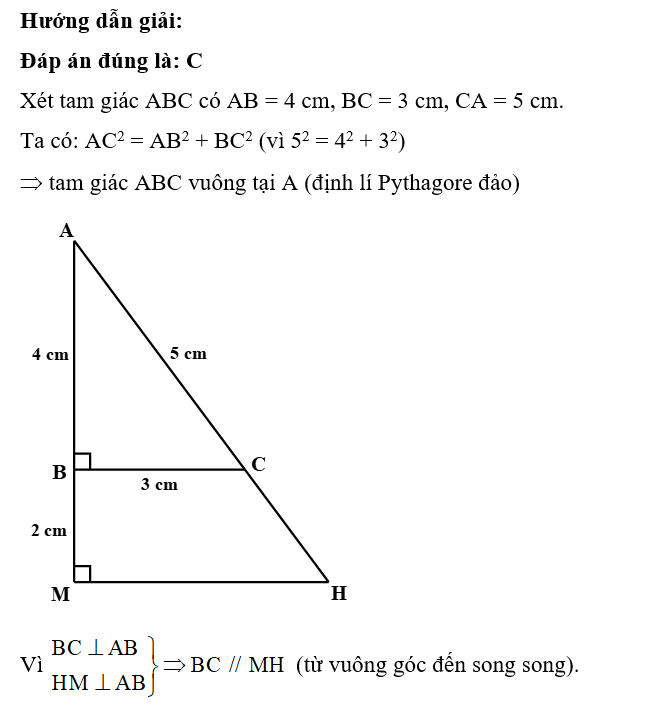
Đáp án đúng là: C

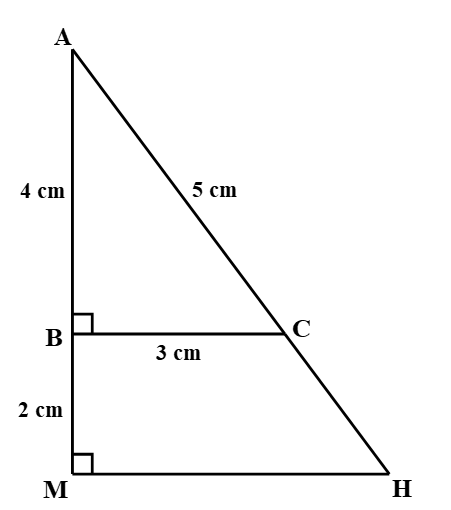
Cho tam giác ABC có độ dài các cạnh AB, BC, CA lần lượt là 4 cm, 3 cm, 5 cm. Trên tia đối của tia BA lấy điểm M sao cho BM (ảnh 1)

Xét tam giác ABC có AB = 4 cm, BC = 3 cm, CA = 5 cm.

Ta có: AC² = AB² + BC² (vì 5² = 4² + 3²)

Þ tam giác ABC vuông tại A (định lí Pythagore đảo)

Vì $\begin{array}{l} B C ⊥ A B \\ H M ⊥ A B \end{array}\} \Rightarrow B C // M H$ (từ vuông góc đến song song).

Vậy BC song song với MH.

Câu 7:

Cho tam giác ABC có độ dài các cạnh AB, BC, CA lần lượt là 4 cm, 3 cm, 5 cm. Trên tia đối của tia BA lấy điểm M sao cho BM = 2 cm, tại M kẻ đường thẳng vuông góc với AB cắt AC tại H. Khẳng định nào sau đây là đúng?

A. $\hat{C A B} + \hat{C H M} = 180 °$ ;

B. $\hat{A B M} + \hat{C H M} = 180 °$ ;

C. $\hat{B C H} + \hat{C H M} = 180 °$ ;

D.

\hat{C A B} + \hat{B A H} = 90 °

.

Xem đáp án

Cho tam giác ABC có độ dài các cạnh AB, BC, CA lần lượt là 4 cm, 3 cm, 5 cm. Trên tia đối của tia BA lấy điểm M sao cho BM (ảnh 2)

Câu 8:

Cho hình vẽ:

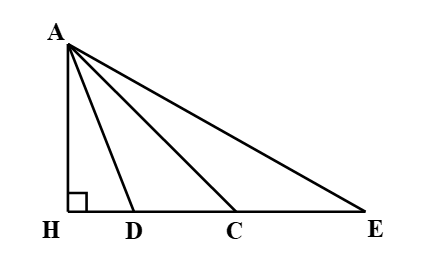
Đoạn thẳng có độ dài ngắn nhất là:

A. AH;

B. AD;

C. AC;

D. AE.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Áp dụng định lí Pythagore vào các tam giác vuông ADH, ACH, AEH ta được:

AD² = AH² + HD²

AC² = AH² + HC²

AE² = AH² + HE²

Vì HD < HC < HE nên AD < AC < AE.

Vậy nhận xét C là đúng.

Vì AH là cạnh góc vuông của các tam giác vuông ADH, ACH, AEH nên

AH < AD < AC < AE.

Vậy đoạn thẳng có độ dài ngắn nhất là AH.

Câu 9:

Cho hình vẽ:

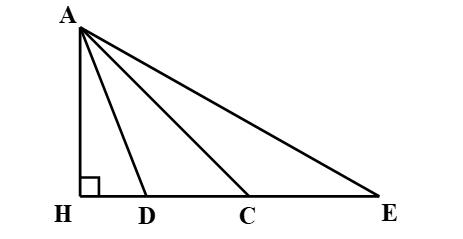
Nhận xét nào sau đây là đúng?

A. Vì HD < HC < HE nên AD > AC > AE;

B. Vì HD > HC > HE nên AD > AC > AE;

C. Vì HD < HC < HE nên AD < AC < AE;

D. Vì HD > HC > HE nên AD < AC < AE.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Áp dụng định lí Pythagore vào các tam giác vuông ADH, ACH, AEH ta được:

AD² = AH² + HD²

AC² = AH² + HC²

AE² = AH² + HE²

Vì HD < HC < HE nên AD < AC < AE.

Vậy nhận xét C là đúng.

Câu 10:

Cho hình vẽ sau

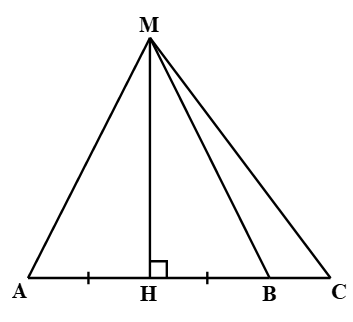
Khẳng định nào sau đây là sai?

A. MA > MH;

B. HB < HC;

C. MA = MB;

D. MC < MA.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

+) Tam giác AMH vuông tại H nên MA > MH.

Þ khẳng định A đúng.

+) Vì B nằm giữa hai điểm H và C nên HB < HC.

Þ khẳng định B đúng.

+) Xét tam giác MAB có MH vuông góc với AB và H là trung điểm của AB.

Þ Tam giác MAB cân tại M

Þ MA = MB

Þ khẳng định C đúng.

+) Áp dụng định lí Pythagore vào tam giác vuông MHB và MHC ta có:

MB² = MH² + HB²

MC² = MH² + HC²

Vì HB < HC nên MB < MC.

Mà MA = MC nên MA < MC.

Þ khẳng định D sai.