Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (0;2;2), B (2;-2;0). Gọi và là tâm của hai đường tròn nằm trên hai mặt phẳng khác nhau và có chung một dây cung AB. Biết rằng luôn có một mặt cầu (S) đi qua cả hai đường tròn ấy. Tính bán kính R của (S).
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
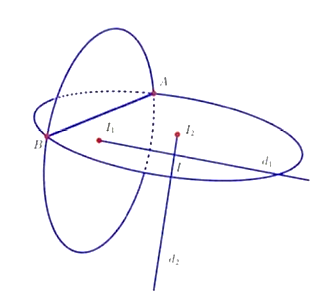
Gọi là đường thẳng đi qua và vuông góc với mặt phẳng , khi đó chứa tâm các mặt cầu đi qua đường tròn tâm .
là đường thẳng đi qua và vuông góc với mặt phẳng , khi đó chứa tâm các mặt cầu đi qua đường tròn tâm .
Do đó, mặt cầu (S) đi qua cả hai đường tròn tâm và có tâm I là giao điểm của , và bán kính R = IA.
Ta có . Đường thẳng có vectơ pháp tuyến là :
.
Phương trình đường thẳng là .
Ta có . Đường thẳng có vectơ pháp tuyến là :
.
Phương trình đường thẳng là .
Xét hệ phương trình . Suy ra .
Bán kính mặt cầu (S) là .
Cho hình trụ có diện tích xung quanh bằng và độ dài đường cao bằng a. Tính bán kính R của đường tròn đáy của hình trụ đã cho theo a.
Có tất cả bao nhiêu cặp số nguyên (x;y) thỏa mãn bất phương trình
?
Có bao nhiêu số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa chữ số 1 và chữ số 3?
Trong không gian với hệ tọa độ Oxyz cho các điểm M (1;-2;3), N (3;0;-1) và I là trung điểm của MN. Mệnh đề nào sau đây đúng?
Cho cấp số nhân với số hạng đầu và công bội q = 2. Hỏi số 1024 là số hạng thứ mấy?
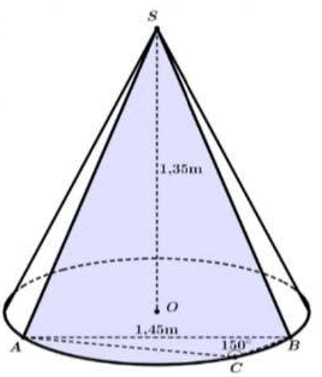
Cửa hàng A có đặt trước sảnh một cái nón lớn với chiều cao 1,35m và sơn cách điệu hoa văn trang trí một phần mặt ngoài của hình nón ứng với cung nhỏ AB như hình vẽ. Biết và giá tiền trang trí là 2.000.000 đồng mỗi mét vuông. Hỏi số tiền mà cửa hàng A cần dùng để trang trí là bao nhiêu?
Trong không gian với hệ tọa độ Oxyz viết phương trình mặt phẳng trung trực của đoạn thẳng PQ với P (1;0;1) và Q (-1;2;3)
Trong không gian với hệ tọa độ Oxyz cho và Tìm tập hợp tất cả các giá trị của x để
Hàm số y = f(x) có đạo hàm liên tục trên ![]() thỏa mãn f(0) = 2 và. Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số , .
thỏa mãn f(0) = 2 và. Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số , .
Cho hàm số bậc bốn có đồ thị như hình vẽ sau
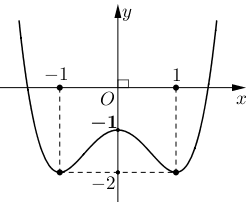
Giá trị cực đại của hàm số là