Cho hàm số y = f(x), y = g(x) có đồ thị như hình sau:
![Cho hàm số y = f(x), y = g(x) có đồ thị như hình sau: Khi đó tổng số nghiệm của hai phương trình f[g(x)]=0 và g[f(x)]=0 là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/02/17-1709002884.png)
Khi đó tổng số nghiệm của hai phương trình và là
A. 26
B. 25
C. 22
D. 21
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C.
Ta có và .
Khi đó .
Số nghiệm của phương trình chính là số giao điểm của đồ thị với đường thẳng với .
Suy ra: phương trình ; ; ; ; có số nghiệm lần lượt là 1;3;3;3;1.
Vậy có tất cả 11 nghiệm.
Tương tự, , phương trình này có 11 nghiệm.
Vậy tổng số nghiệm của hai phương trình và là 22.
Cho hàm số có ba điểm cực trị là -1, 1 và 3. Gọi y = g(x) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số y = f(x). Diện tích hình phẳng giới hạn bởi hai đường y = f(x) và y = g(x) bằng
Trong không gian Oxyz, hình chiếu vuông góc của điểm A(3;5;2) trên trục Ox có tọa độ là
Tìm m để giá trị lớn nhất của hàm số trên đoạn [0;2] là nhỏ nhất. Giá trị của m thuộc khoảng nào?
Có bao nhiêu số nguyên dương m nhỏ hơn 20 thỏa mãn phương trình có đúng hai nghiệm thực phân biệt.
Tìm m để giá trị lớn nhất của hàm số trên đoạn [0;2] là nhỏ nhất. Giá trị của m thuộc khoảng nào?
Cho hàm số y = f(x) liên tục trên thỏa mãn . Giá trị tích phân bằng
Cho hàm số trùng phương có đồ thị như hình vẽ.
![Cho hàm số trùng phương y = ã^4 + bx^2 + c có đồ thị như hình vẽ. Hỏi đồ thị hàm số y=(x^2-4)(x^2+2x)/[f(x)]^2+2f(x)-3 có tổng cộng bao nhiêu tiệm cận (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/02/13-1709001015.png)
Hỏi đồ thị hàm số có tổng cộng bao nhiêu tiệm cận đứng?
Có hai hộp bút chì màu, các bút chì khác nhau. Hộp thứ nhất có 5 bút chì màu đỏ và 7 bút chì màu xanh. Hộp thứ hai có 8 bút chì màu đỏ và 4 bút chì màu xanh. Chọn ngẫu nhiên mỗi hộp một cây bút chì. Xác suất để chọn một cây bút chì màu đỏ và một bút chì màu xanh là
Cho hàm số y = f(x) đồng biến trên liên tục, nhận giá trị dương trên thỏa mãn và . Tính f(8) .
Cho hàm f(x) xác định trên có bảng xét dấu f’(x) như sau
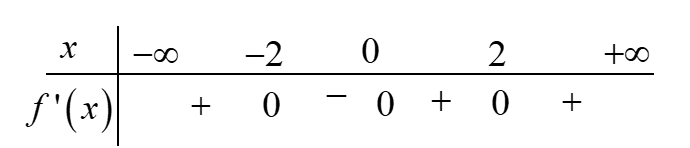
Số điểm cực trị của hàm số đã cho là
Cho một cấp số cộng có số hạng đầu và công sai d , số hạng tổng quát được xác định bởi công thức
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a, chiều cao h. Khi đó thể tích khối lăng trụ là
Từ các số 1;2;3;4;5 có thể lập được bao nhiêu số tự nhiên gồm chữ số đôi một khác nhau?
Trong không gian Oxyz, cho hai điểm A(1;1;-2), B(2;2;1). Vectơ có tọa độ là