Góc giữa hai đường thẳng bất kì trong không gian là góc giữa

Trong các hàm số sau đây hàm số nào không phải là hàm số mũ?

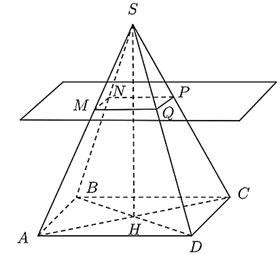
Cho hình chóp tứ giác đều $S.ABCD$. Cắt hình chóp bởi mặt phẳng song song với đáy và cắt tất cả các cạnh bên của hình chóp thì ta được

Tập nghiệm của bất phương trình \[{\log _2}x < 1\] là

Cho $x$, $y$ là hai số thực dương khác \[1\] và $m$, $n$ là hai số thực tùy ý. Đẳng thức nào sau đây là sai?

Cho hai đường thẳng \[{d_1}\] và ${d_2}$ chéo nhau. Mệnh đề nào sau đây đúng?

Cho hình chóp \[S.ABCD\] có \[SA \bot \left( {ABCD} \right)\] đáy \[ABCD\] là hình thoi. Góc \[BAC\] là một góc phẳng của góc nhị diện nào sau đây?

Cho \[a > 0\], \[b > 0\] và \[{a^2} + {b^2} = 7ab\]. Đẳng thức nào dưới đây là đúng?

Chọn mệnh đề đúng trong các mệnh đề sau?

Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$. Hãy chọn khẳng định đúng?

Cho hình lập phương \[ABCD.A'B'C'D'\] cạnh $a$. Gọi \[\alpha \] là góc giữa \[AC\] và mặt phẳng \[\left( {A'BCD'} \right).\] Chọn khẳng định đúng trong các khẳng định sau.

Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a\], \[SA = a\] và \[SA\] vuông góc với mặt đáy. \[M\] là trung điểm \[SD\]. Tính theo a khoảng cách giữa hai đường thẳng \[SB\] và \[CM\].

Cho $0 < a \ne 1,\,M > 0$ và $\alpha $ là số thực tùy ý. Mệnh đề nào sau đây là sai?

Chị Hà gửi vào ngân hàng $20\,\,000\,\,000$ đồng với lãi suất \[0,5\% \]/tháng (sau mỗi tháng tiền lãi được nhập vào tiền gốc để tính lãi tháng sau). Hỏi sau \[1\] năm chị Hà nhận được bao nhiêu tiền, biết trong \[1\] năm đó chị Hà không rút tiền lần nào và lãi suất không thay đổi (làm tròn đến hàng nghìn).

Trong các phương trình sau, phương trình nào là phương trình mũ?

Mệnh đề nào sau đây đúng?