Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a\], \[SA = a\] và \[SA\] vuông góc với mặt đáy. \[M\] là trung điểm \[SD\]. Tính theo a khoảng cách giữa hai đường thẳng \[SB\] và \[CM\].
Giải bởi Vietjack
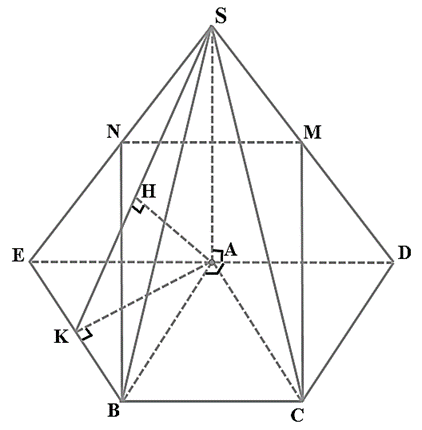
Gọi \[E\] là điểm đối xứng với \[D\] qua \[A\],\[N\] là trung điểm của \[SE\] và \[K\] là trung điểm của \[BE\].
Ta có các tứ giác \[NMCB\] và \[ACBE\] là các hình bình hành.
Có \[CM{\text{//}}\,\left( {SBE} \right)\] nên \[d\left( {CM,SB} \right) = d\left( {CM,\left( {SBE} \right)} \right) = d\left( {C,\left( {SBE} \right)} \right) = d\left( {A,\left( {SBE} \right)} \right)\].
$\Delta ABE$ vuông cân tại \[A\] có \[AB = a\] nên $AK \bot BE$.
Kẻ \[AH \bot SK\], \[H \in SK\].
Có \[\left\{ \begin{gathered}
BE \bot AK \hfill \\
BE \bot SA \hfill \\
\end{gathered} \right. \Rightarrow BE \bot \left( {SAK} \right)\]\[ \Rightarrow BE \bot AH\].
Có \[\left\{ \begin{gathered}
AH \bot BE \hfill \\
AH \bot SK \hfill \\
\end{gathered} \right.\]\[ \Rightarrow AH \bot \left( {SBE} \right) \Rightarrow d\left( {A,\left( {SBE} \right)} \right) = AH\].
Ta có \[AK = \frac{{a\sqrt 2 }}{2}\], \[SK = \sqrt {S{A^2} + A{K^2}} = \frac{{a\sqrt 3 }}{{\sqrt 2 }}\];
\[AH = \frac{{SA \cdot AK}}{{SK}}\]$ = \frac{{a \cdot \frac{{a\sqrt 2 }}{2}}}{{\frac{{a\sqrt 3 }}{{\sqrt 2 }}}} = \frac{{a\sqrt 3 }}{3}$.
Vậy \[d\left( {CM,SB} \right) = \frac{{a\sqrt 3 }}{3}\].
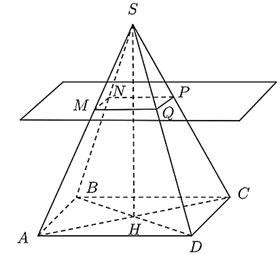
Cho hình chóp tứ giác đều $S.ABCD$. Cắt hình chóp bởi mặt phẳng song song với đáy và cắt tất cả các cạnh bên của hình chóp thì ta được
Cho hai đường thẳng \[{d_1}\] và ${d_2}$ chéo nhau. Mệnh đề nào sau đây đúng?
Cho $x$, $y$ là hai số thực dương khác \[1\] và $m$, $n$ là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
Cho hình chóp \[S.ABCD\] có \[SA \bot \left( {ABCD} \right)\] đáy \[ABCD\] là hình thoi. Góc \[BAC\] là một góc phẳng của góc nhị diện nào sau đây?
Cho \[a > 0\], \[b > 0\] và \[{a^2} + {b^2} = 7ab\]. Đẳng thức nào dưới đây là đúng?
Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$. Hãy chọn khẳng định đúng?
Cho hình lập phương \[ABCD.A'B'C'D'\] cạnh $a$. Gọi \[\alpha \] là góc giữa \[AC\] và mặt phẳng \[\left( {A'BCD'} \right).\] Chọn khẳng định đúng trong các khẳng định sau.
Cho $0 < a \ne 1,\,M > 0$ và $\alpha $ là số thực tùy ý. Mệnh đề nào sau đây là sai?
Chị Hà gửi vào ngân hàng $20\,\,000\,\,000$ đồng với lãi suất \[0,5\% \]/tháng (sau mỗi tháng tiền lãi được nhập vào tiền gốc để tính lãi tháng sau). Hỏi sau \[1\] năm chị Hà nhận được bao nhiêu tiền, biết trong \[1\] năm đó chị Hà không rút tiền lần nào và lãi suất không thay đổi (làm tròn đến hàng nghìn).
độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng quãng đường bóng đã di chuyển (từ lúc bắt đầu thả đến lúc bóng không di chuyển nữa) gần nhất với kết quả nào sau đây?
. Tính tổng 
, trong đó a là tham số thực. Tìm a để 
bằng:
là:
là:
bằng
bằng