Trong mặt phẳng tọa độ \(Oxy,\)cho đường tròn lượng giác như hình vẽ bên dưới.
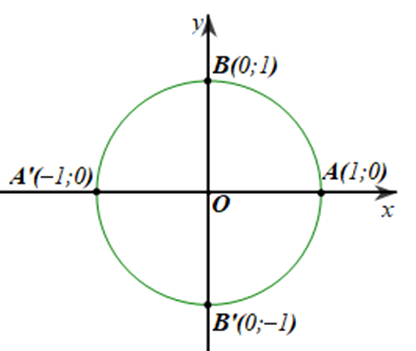
Hỏi góc lượng giác nào sau đây có số đo là \( - 90^\circ \)?
D. \(\left( {OA,OA} \right)\).
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
Đơn giản biểu thức \(A = \cos \left( {\frac{{9\pi }}{2} - \alpha } \right) + \sin \left( {\alpha - \pi } \right)\) ta được
Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ \(t\) của năm 2023 (có 365 ngày) được cho bởi một hàm số \(y = 4\sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] + 10\), với \(t \in \mathbb{Z}\) và \[0 < t \le 365\]. Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) trong không gian. Có bao nhiêu vị trí tương đối của \(a\) và \(\left( P \right)\)?
Cho mặt phẳng \[\left( \alpha \right)\] và đường thẳng \[d \not\subset \left( \alpha \right)\]. Khẳng định nào sau đây là sai?
Cho tứ diện \(ABCD\), gọi \({G_1},{G_2}\) lần lượt là trọng tâm tam giác \(BCD\) và \(ACD.\) Mệnh đề nào sau đây sai?
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\), gọi \(I\) là trung điểm cạnh \(SC\). Mệnh đề nào sau đây sai?
Giải các phương trình lượng giác:
a) \(\sin \left( {2x + \frac{\pi }{4}} \right) + \cos x = 0\);
b) \(\frac{1}{{{{\sin }^2}x}} - \left( {\sqrt 3 - 1} \right)\cot x - \left( {\sqrt 3 + 1} \right) = 0\) và \(x \in \left( {0;\pi } \right)\).
Trong không gian, cho ba đường thẳng \(a,\,\,b,\,\,c\). Trong các mệnh đề sau mệnh đề nào đúng?
Trong không gian cho các mệnh đề sau:
(I) Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì song song với nhau.
(II) Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó.
(III) Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy song song với nhau.
(IV) Qua điểm \(A\) không thuộc đường thẳng \[d\], kẻ được đúng một đường thẳng song song với \[d\].
Số mệnh đề đúng là
Cho hình chóp \[S.ABCD\]. Gọi \[I,J\] lần lượt là trung điểm của \[AB\] và \[BC\]. Giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SIJ} \right)\] là một đường thẳng song song với
Cho tứ diện \[ABCD.\] Gọi \[E\] và \[F\] lần lượt là trung điểm của \[AB\] và \[CD\]; \[G\] là trọng tâm tam giác \[BCD.\] Giao điểm của đường thẳng \[EG\] và mặt phẳng \[\left( {ACD} \right)\] là
Cho tứ diện \(ABCD\) và điểm \(M\) thuộc cạnh \(AB\). Gọi \(\left( \alpha \right)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(BC\) và \(AD\). Gọi \(N,P,Q\) lần lượt là giao điểm của mặt phẳng \(\left( \alpha \right)\) với các cạnh \(AC,CD\) và \(DB\).
a) Chứng minh \(MNPQ\) là hình bình hành.
b) Trong trường hợp nào thì \(MNPQ\) là hình thoi?
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và \({u_2} = 8\). Công sai của cấp số cộng đã cho bằng