Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AC = 4a\,,\,\,BC = 2a.\) Đỉnh \(S\) cách đều các đỉnh \[A,\,\,B,\,\,C,\,\,D.\] Biết góc giữa mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng \(60^\circ .\) Thể tích khối chóp đã cho bằng
 Giải bởi Vietjack
Giải bởi Vietjack
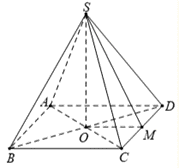
Gọi \(O\) là tâm của hình chữ nhật \(ABCD\).
Suy ra \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot CD\).
Gọi \(M\) là trung điểm của \(CD \Rightarrow OM \bot CD\)
Do đó \(CD \bot \left( {SMO} \right)\) mà \(\left\{ {\begin{array}{*{20}{l}}{\left( {SMO} \right) \cap \left( {SCD} \right) = SM}\\{\left( {SMO} \right) \cap \left( {ABCD} \right) = OM}\end{array}} \right.\)
Suy ra \(\left( {\widehat {\left( {SCD} \right),\,\,\left( {ABCD} \right)}} \right) = \left( {\widehat {SM\,;\,OM}} \right) = \widehat {SMO} = 60^\circ .\)Ta có \(OM = \frac{1}{2}BC = \frac{1}{2} \cdot 2a = a \Rightarrow SO = OM \cdot \tan \widehat {SMO}\)
\( \Rightarrow SO = \sqrt 3 a \Rightarrow {V_{S \cdot ABCD}} = \frac{1}{3} \cdot SO \cdot {S_{ABCD}} = \frac{1}{3} \cdot \sqrt 3 a \cdot 8{a^2} = \frac{{8\sqrt 3 {a^3}}}{3}.\) Chọn A.
Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số \(h\left( t \right) = 90\cos \left( {\frac{\pi }{{10}}t} \right)\), trong đó \[h\left( t \right)\] là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm \(t\) giây. Chiều cao của sóng (tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng) bằng
Cho hàm số , với \(m\) là tham số. Gọi \({m_1},\,\,{m_2}\,\,\left( {{m_1} < {m_2}} \right)\) là các giá trị của tham số \(m\) thỏa mãn \(2{\max _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) - {\min _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) = 8.\) Tổng \(2{m_1} + 3{m_2}\) bằng
Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = \frac{{\sqrt {x + 2} }}{{\sqrt {{x^2} - 6x + 2m} }}\) có hai đường tiệm cận đứng. Số phần tử của \(S\) là
Hỗn hợp X gồm 2 ester đơn chức (không chứa nhóm chức nào khác). Cho 0,08 mol X tác dụng hết với dung dịch \[AgN{O_3}/N{H_3}\]thu được 0,16 mol Ag. Mặt khác thủy phân hoàn toàn 0,08 mol X bằng dung dịch NaOH dư thu được dung dịch chứa 9,34 gam hỗn hợp 2 muối và 1,6 gam \[C{H_3}OH.\]Phần trăm khối lượng ester có phân tử khối lớn hơn trong X là
Mỗi học sinh lớp 10B đều chơi bóng đá hoặc bóng chuyền. Biết rằng có 25 bạn chơi bóng đá, 20 bạn chơi bóng chuyền và 10 bạn chơi cả hai môn. Hỏi lớp 10B có bao nhiêu học sinh?
Trong không gian \[Oxyz,\] cho hai điểm \(A\left( {2\,;\,\, - 2\,;\,\,1} \right),\,\,B\left( {0\,;\,\,1\,;\,\,2} \right).\) Tọa độ điểm \(M\) thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho ba điểm \[A,\,\,B,\,\,M\] thẳng hàng là
Cho hàm số \(f\left( x \right)\) có đạo hàm là \(f'\left( x \right) = \left( {x - 1} \right)\left( {x - m} \right)\) với \(m\) là tham số thực. Tìm tất cả các giá trị của \(m\) để hàm số đồng biến trên \(\left( { - \infty \,;\,\, + \infty } \right)\)?
Trong không gian \[Oxyz,\] cho điểm \(H\left( {1\,;\,\,2\,;\,\, - 2} \right).\) Mặt phẳng \[\left( \alpha \right)\] đi qua \[H\] và cắt các trục \[Ox,\,\,Oy,\,\,Oz\] tại \[A,\,\,B,\,\,C\] sao cho H là trực tâm tam giác \[ABC.\] Phương trình mặt cầu tâm \(O\) và tiếp xúc với mặt phẳng \[\left( \alpha \right)\] là
Gọi \(S\) là diện tích hình phẳng giới hạn bởi parabol \(y = {x^2} + 2x - 1\) và các đường thẳng \(y = m\,,\,\,x = 0\,,\,\,x = 1.\) Để \(S \le 2021\) thì có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 4040\,;\,\, - 3} \right]?\)
Cho hàm số \(y = \frac{{x + 2}}{{2x + 3}}\) (1). Đường thẳng \(d:y = ax + b\) là tiếp tuyến của đồ thị hàm số (1). Biết \(d\) cắt trục hoành, trục tung lần lượt tại hai điểm \[A,\,\,B\] sao cho \(\Delta OAB\) cân tại \[O.\] Khi đó \(a + b\) bằng
Có bao nhiêu giá trị nguyên âm của tham số \(m\) để hàm số \(y = \left| {{x^5} + 2{x^4} - m{x^2} + 3x - 20} \right|\) nghịch biến trên khoảng \(\left( { - \infty \,;\,\, - 2} \right)\)?
Số nghiệm nguyên \(x\) của thoả mãn \(\left( {{3^{{x^2} - 1}} - {{27}^{x + 1}}} \right)\left[ {{{\log }_3}\left( {x + 8} \right) - 2} \right] \le 0\) là
Quá trình hình thành các loài B, C, D từ loài A (loài gốc) được mô tả ở hình bên. Phân tích hình này, theo lí thuyết, có bao nhiêu phát biểu sau đây đúng?
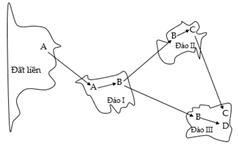
I. Các cá thể của loài B ở đảo II có thể mang một số alen đặc trưng mà các cá thể của loài B ở đảo I không có.
II. Khoảng cách giữa các đảo có thể là yếu tố duy trì sự khác biệt về vốn gen giữa các quần thể ở đảo I, đảo II và đảo III.
III. Vốn gen của các quần thể thuộc loài B ở đảo I, đảo II và đảo III phân hóa theo cùng 1 hướng.
IV. Điều kiện địa lí ở các đảo là nhân tố trực tiếp gây ra những thay đổi về vốn gen của mỗi quần thể.