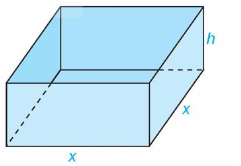
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng ![]() cm2 như hình dưới đây.
cm2 như hình dưới đây.
Biết khi ![]() thì thể tích của hộp là lớn nhất. Khi đó
thì thể tích của hộp là lớn nhất. Khi đó ![]() bằng bao nhiêu?
bằng bao nhiêu?
 Giải bởi Vietjack
Giải bởi Vietjack
Hình hộp trên có độ dài cạnh đáy là ![]() (cm,
(cm, ![]() ) và chiều cao là
) và chiều cao là ![]() (cm,
(cm, ![]() ).
).
Diện tích bề mặt của hình hộp là ![]() cm2 nên
cm2 nên ![]() .
.
Suy ra 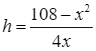 (cm).
(cm).
Thể tích của hình hộp là: 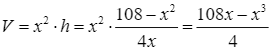 (cm3).
(cm3).
Xét hàm số 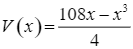 với
với ![]() .
.
Ta có: 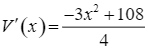 . Trên khoảng
. Trên khoảng ![]() ,
, ![]() .
.
Bảng biến thiên của hàm số ![]() như sau:
như sau:
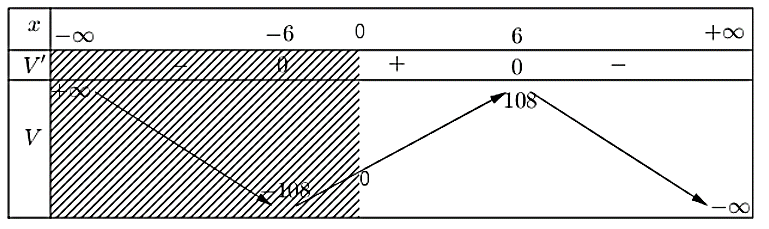
Do đó, thể tích của hình hộp lớn nhất khi độ dài cạnh đáy là ![]() cm.
cm.
Khi đó, chiều cao của hình hộp là 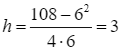 (cm).
(cm).
Vậy ![]() và
và ![]() .
.
Đáp số: ![]() .
.
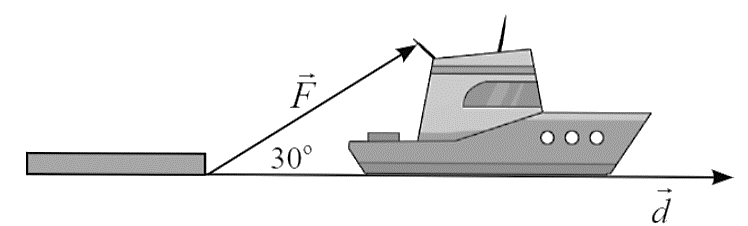
Một tàu kéo một xà lan trên biển di chuyển được 5 km với một lực kéo có cường độ ![]() N và có phương hợp với phương dịch chuyển một góc
N và có phương hợp với phương dịch chuyển một góc ![]() . Công thực hiện bởi lực kéo nói trên bằng bao nhiêu Jun (làm tròn kết quả đến hàng đơn vị)?
. Công thực hiện bởi lực kéo nói trên bằng bao nhiêu Jun (làm tròn kết quả đến hàng đơn vị)?
Cho hàm số ![]() xác định và liên tục trên
xác định và liên tục trên ![]() có đồ thị hàm số như hình vẽ dưới đây.
có đồ thị hàm số như hình vẽ dưới đây.
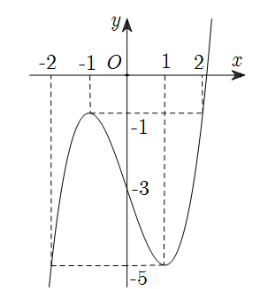
Giá trị nhỏ nhất ![]() và giá trị lớn nhất
và giá trị lớn nhất ![]() của hàm số đã cho trên đoạn
của hàm số đã cho trên đoạn ![]() lần lượt là:
lần lượt là:
Cho tứ diện \(ABCD\) và điểm \(G\) thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \) (\(G\) là trọng tâm của tứ diện). Gọi \({G_0}\) là giao điểm của \(GA\) và mặt phẳng \(\left( {BCD} \right)\). Trong các khẳng định sau, khẳng định nào đúng?
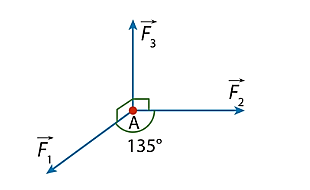
Một chất điểm ![]() nằm trên mặt phẳng nằm ngang
nằm trên mặt phẳng nằm ngang ![]() , chịu tác động bởi ba lực
, chịu tác động bởi ba lực ![]() . Các lực
. Các lực ![]() có giá nằm trong
có giá nằm trong ![]() và
và ![]() , còn lực
, còn lực ![]() có giá vuông góc với
có giá vuông góc với ![]() và hướng lên trên. Độ lớn hợp lực của các lực
và hướng lên trên. Độ lớn hợp lực của các lực ![]() bằng bao nhiêu (làm tròn kết quả đến hàng phần mười), biết rằng độ lớn của ba lực đó lần lượt là 20 N, 15 N và 10 N.
bằng bao nhiêu (làm tròn kết quả đến hàng phần mười), biết rằng độ lớn của ba lực đó lần lượt là 20 N, 15 N và 10 N.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:
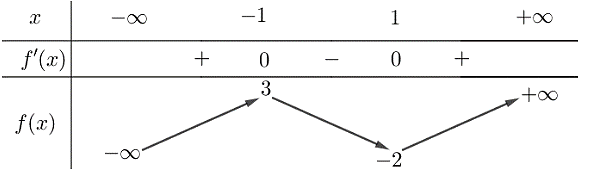
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:
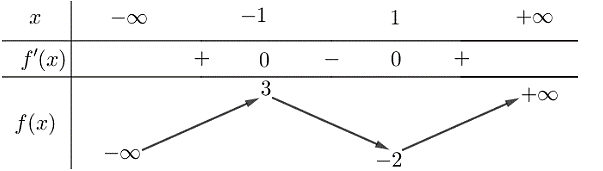
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số ![]() xác định trên
xác định trên ![]() và có đồ thị như hình dưới đây.
và có đồ thị như hình dưới đây.
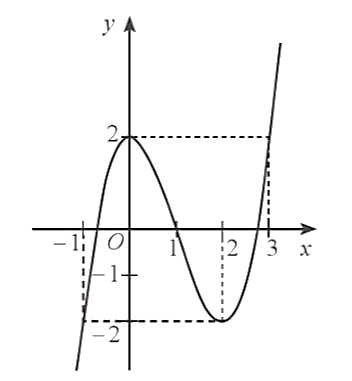
a) Hàm số đã cho nghịch biến trên các khoảng ![]() và
và ![]() .
.
b) Hàm số đã cho có ![]() điểm cực trị.
điểm cực trị.
c) Trên đoạn ![]() , giá trị lớn nhất của hàm số đã cho bằng
, giá trị lớn nhất của hàm số đã cho bằng ![]() .
.
d) Phương trình ![]() có duy nhất 1 nghiệm.
có duy nhất 1 nghiệm.