Cho hàm số ![]() :
: 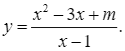
Khảo sát và vẽ đồ thị hàm số ![]() với
với ![]()
 Giải bởi Vietjack
Giải bởi Vietjack
Với \(m = - 4\), ta có: \(\left( C \right):y = \frac{{{x^2} - 3x - 4}}{{x - 1}}\).
1. Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)
2. Sự biến thiên
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 3x - 4}}{{x - 1}} = + \infty .\)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} - 3x - 4}}{{x - 1}} = - \infty .\)
Do đó, đồ thị hàm số không có tiệm cận ngang.
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 3x - 4}}{{x - 1}} = - \infty ,\)\(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 3x - 4}}{{x - 1}} = + \infty \), do đó đồ thị hàm số nhận đường thẳng \(x = 1\) làm tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 3x - 4}}{{x\left( {x - 1} \right)}} = 1\), \(\mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{{x^2} - 3x - 4}}{{x - 1}} - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 2x - 4}}{{x - 1}} = - 2\).
Do đó, đồ thị hàm số nhận đường thẳng \(y = x - 2\) làm tiệm cận xiên.
Ta có: \(y' = \frac{{{x^2} - 2x + 7}}{{{{\left( {x - 1} \right)}^2}}} > 0,\forall x \in D.\)
Từ đây ta có bảng biến thiên:
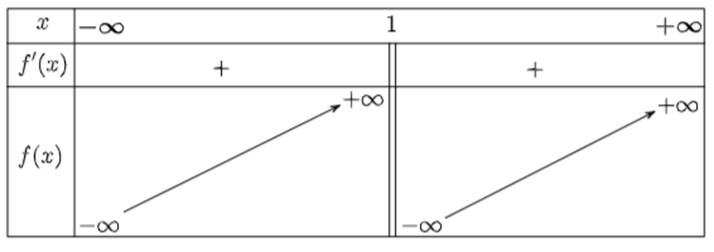
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)
Hàm số không có cực trị.
3. Đồ thị
Giao điểm của đồ thị với trục tung: \(\left( {0;4} \right).\)
Giao điểm của đồ thị với trục hoành: \(\left( {4;0} \right),\left( { - 1;0} \right).\)
Đồ thị đi qua các điểm \(\left( { - 2; - 2} \right);\left( {2; - 6} \right);\left( {3; - 2} \right);\left( {5;\frac{3}{2}} \right)\).
Đồ thị nhận đường thẳng \(x = 1\) làm tiệm cận đứng và đường thẳng \(y = x - 2\) làm tiệm cận xiên.
Ta có đồ thị hàm số:
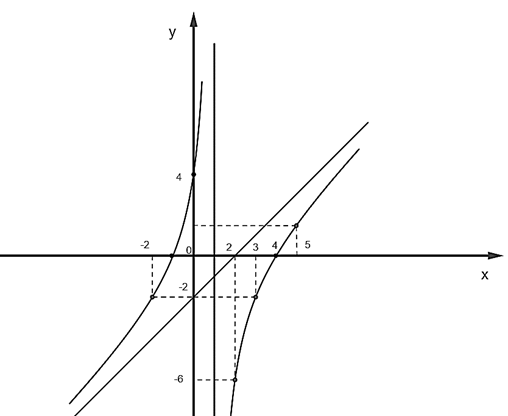
Hiệu số giữa giá trị cực đại và giá trị cực tiểu của hàm số \(f\left( x \right) = {x^3} - 3{x^2} + 4\) là:
Cho hàm số ![]() liên tục trên
liên tục trên ![]() và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
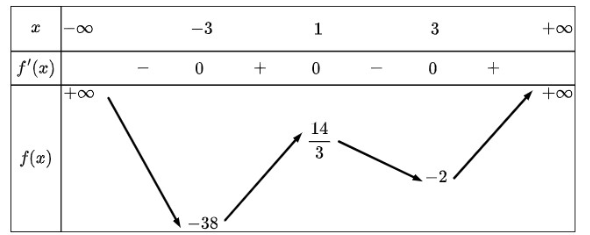
Đồ thị của hàm số trên cắt trục hoành tại mấy điểm?
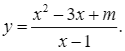
Một chất điểm chuyển động trong ![]() giây đầu tiên có phương trình như sau:
giây đầu tiên có phương trình như sau:
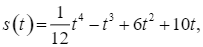
trong đó ![]() với
với ![]() tính bằng giây
tính bằng giây ![]() và
và ![]() tính bằng mét
tính bằng mét ![]() . Hỏi tại thời điểm gia tốc đạt giá trị nhỏ nhất thì vận tốc bằng bao nhiêu?
. Hỏi tại thời điểm gia tốc đạt giá trị nhỏ nhất thì vận tốc bằng bao nhiêu?
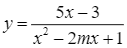 không có tiệm cận đứng.
không có tiệm cận đứng.Độ giảm huyết áp của một bệnh nhân được cho bởi công thức sau:
\(G\left( x \right) = 0,025{x^2}\left( {30 - x} \right),\)
trong đó \(x\)là lượng thuốc được tiêm cho bệnh nhân (\(x\) được tính bằng miligam).
Liều lượng thuốc cần tiêm cho bệnh nhân nằm trong khoảng nào để huyết áp bệnh nhân tăng?
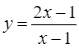 có đồ thị
có đồ thị Hàm số ![]() có đồ thị hàm số như hình vẽ.
có đồ thị hàm số như hình vẽ.
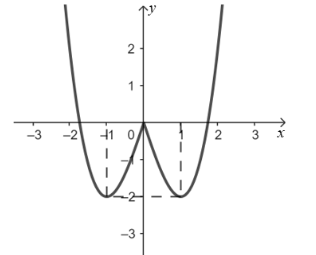
Khẳng định nào sau đây là đúng?