Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB\, = a\), \(AA' = a\sqrt 2 \).
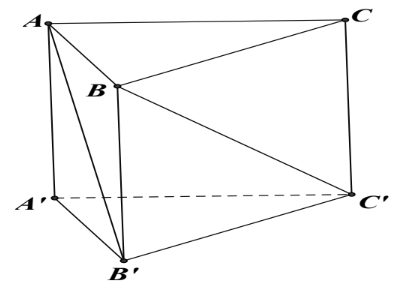
a) \(\overrightarrow {AB'} = \overrightarrow {AB} + \overrightarrow {CC'} \).
b) \(\left| {\overrightarrow {AB'} } \right| = \left| {\overrightarrow {BC'} } \right| = \sqrt 3 \).
c) \(\overrightarrow {AB'} \cdot \overrightarrow {BC'} = \frac{{{a^2}}}{2}\).
d) \(\left( {\overrightarrow {AB'} ,\,\overrightarrow {BC'} } \right) = 60^\circ \).
Giải bởi Vietjack
a) Đ, b) Đ, c) S, d) Đ.
Hướng dẫn giải
– Vì \(ABC.A'B'C'\) là lăng trụ tam giác đều nên \(\overrightarrow {CC'} = \overrightarrow {BB'} \).
Theo quy tắc ba điểm ta có: \(\overrightarrow {AB'} = \overrightarrow {AB} + \overrightarrow {BB'} = \overrightarrow {AB} + \overrightarrow {CC'} \). Vậy ý a) đúng.
– Ta có \(ABB'A',\,\,BCC'B'\) là các hình chữ nhật có hai kích thước là \(a\) và \(a\sqrt 2 \).
Do đó, \(AB' = BC' = \sqrt {{a^2} + {{\left( {a\sqrt 2 } \right)}^2}} = a\sqrt 3 \). Suy ra \(\left| {\overrightarrow {AB'} } \right| = \left| {\overrightarrow {BC'} } \right| = \sqrt 3 \).
Vậy ý b) đúng.
– Ta có \(\overrightarrow {AB'} \cdot \overrightarrow {BC'} = \left( {\overrightarrow {AB} + \overrightarrow {BB'} } \right) \cdot \left( {\overrightarrow {BC} + \overrightarrow {CC'} } \right)\)
\( = \overrightarrow {AB} \cdot \overrightarrow {BC} + \overrightarrow {AB} \cdot \overrightarrow {CC'} + \overrightarrow {BB'} \cdot \overrightarrow {BC} + \overrightarrow {BB'} \cdot \overrightarrow {CC'} \)
\( = - AB \cdot BC \cdot \cos \widehat {BAC} + 0 + 0 + B{B'^2}\)
\( = - a \cdot a \cdot \cos 60^\circ + {\left( {a\sqrt 2 } \right)^2}\)\( = \frac{{3{a^2}}}{2}\).
Suy ra \(\cos \left( {\overrightarrow {AB'} ,\,\overrightarrow {BC'} } \right) = \frac{{\overrightarrow {AB'} \cdot \,\overrightarrow {BC'} }}{{\left| {\overrightarrow {AB'} } \right| \cdot \,\left| {\overrightarrow {BC'} } \right|}} = \frac{{\frac{{3{a^2}}}{2}}}{{a\sqrt 3 \cdot a\sqrt 3 }} = \frac{1}{2}\). Do đó, \(\left( {\overrightarrow {AB'} ,\,\overrightarrow {BC'} } \right) = 60^\circ \).
Vậy ý c) sai và ý d) đúng.
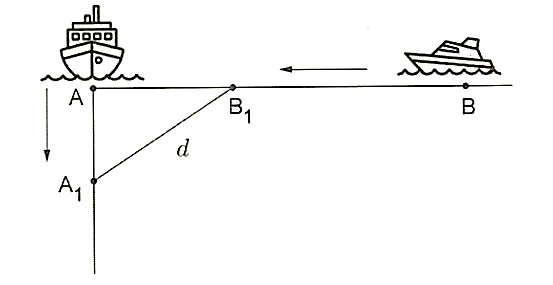
Hai con tàu \[A\] và \(B\) đang ở cùng một vĩ tuyến và cách nhau 5 hải lí. Cả hai tàu đồng thời cùng khởi hành. Tàu \[A\] chạy về hướng Nam với vận tốc 6 hải lí/giờ, còn tàu \[B\] chạy về vị trí hiện tại của tàu \[A\] với vận tốc 7 hải lí/giờ (tham khảo hình vẽ). Hỏi sau bao nhiêu giờ thì khoảng cách giữa hai tàu là bé nhất (làm tròn kết quả đến hàng phần mười)?
Cho hàm số \(y = \frac{{ - {x^2} + x + 1}}{{x + 1}}\) có đồ thị \(\left( C \right)\).
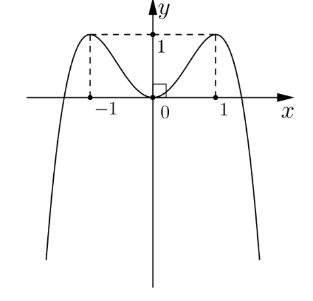
a) Hàm số đã cho nghịch biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {0; + \infty } \right)\).
b) Đồ thị \(\left( C \right)\) có hai điểm cực trị nằm ở hai phía đối với trục tung.
c) Đồ thị \(\left( C \right)\) có đường tiệm cận đứng là \(x = - 1\); đường tiệm cận xiên là \(y = - x + 2\).
d) Đồ thị \(\left( C \right)\) nhận điểm \(I\left( { - 1;3} \right)\) làm tâm đối xứng.
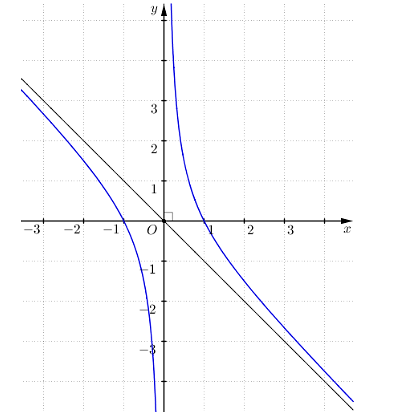
Đường cong trong hình dưới đây là đồ thị của hàm số nào trong bốn hàm số ở các phương án A, B, C, D.
Một chất điểm ở vị trí đỉnh \(A\) của hình lập phương \(ABCD.A'B'C'D'\). Chất điểm chịu tác động bởi ba lực \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \) lần lượt cùng hướng với \(\overrightarrow {AD} ,\,\overrightarrow {AB} ,\,\overrightarrow {AC'} \) như hình vẽ.
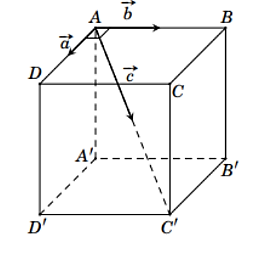
Độ lớn của các lực \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \) tương ứng là 10 N, 10 N và 20 N. Độ lớn hợp lực của các lực \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \) bằng bao nhiêu Newton (làm tròn kết quả đến hàng phần mười)?
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên trên \(\left[ { - 5;7} \right)\) như sau:
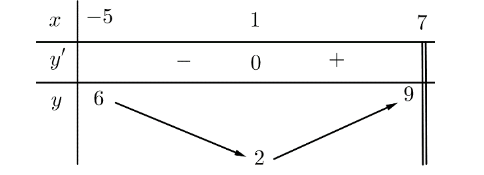
Mệnh đề nào dưới đây là đúng?
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{ax + 1}}{{bx + c}}\) (\(a,\,b,\,c\) là các tham số) có bảng biến thiên như sau:
a) Hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
b) Hàm số đã cho có \(2\) điểm cực trị.
c) Trên khoảng \(\left( {2; + \infty } \right)\), giá trị lớn nhất của hàm số đã cho bằng \(1\).
d) Giá trị của biểu thức \(a + b + c\) bằng \(0\).
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \[y = f\left( x \right)\] có đồ thị là đường cong như hình dưới đây.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
