B. Hàm số đạt giá trị nhỏ nhất bằng \(\frac{3}{4}\) và giá trị lớn nhất bằng \(1\).
C. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất.
D. Hàm số đạt giá trị lớn nhất tại điểm có hoành độ \(x = 1\) và giá trị lớn nhất bằng \(1\).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Tập xác định: \(D = \left[ {1; + \infty } \right)\).
Ta có: \(y' = 1 - \frac{1}{{2\sqrt {x - 1} }} = \frac{{2\sqrt {x - 1} - 1}}{{2\sqrt {x - 1} }}\).
\(y' = 0 \Leftrightarrow \frac{{2\sqrt {x - 1} - 1}}{{2\sqrt {x - 1} }} = 0\)\( \Leftrightarrow 2\sqrt {x - 1} = 1 \Leftrightarrow x = \frac{5}{4}\).
Ta có bảng biến thiên như sau:
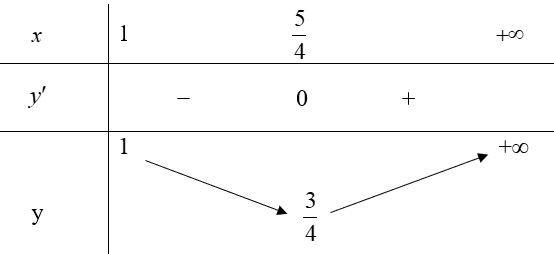
Từ bảng biến thiên ta thấy:
Hàm số có giá trị nhỏ nhất là \(\frac{3}{4}\) và không có giá trị lớn nhất.
Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\mathbb{R}\) và có bảng xét dấu \(f'\left( x \right)\) dưới đây:
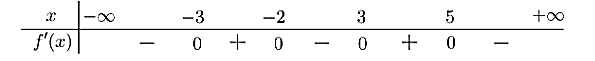
Số điểm cực trị của hàm số đã cho là:
Thể tích \(V\) (đơn vị: cm3) của 1 kg nước tại nhiệt độ \(T\left( {0^\circ C \le T \le 30^\circ C} \right)\) được tính bởi công thức sau: \(V(T) = 999,87 - 0,06426T + 0,0085043{T^2} - 0,0000679{T^3}.\) (Nguồn: J. Stewart, Calculus, Steventh Edition, Brooks/Cole, CENGAGE Learning 2012).
Hỏi thể tích \(V\left( T \right)\),\(\left( {0^\circ C \le T \le 30^\circ C} \right)\), giảm trong khoảng nhiệt độ gần với khoảng nào sau đây?
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\).
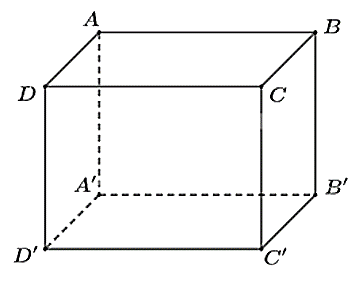
Mệnh đề nào sau đây là sai?
Trong không gian \[Oxyz\], cho hai vectơ \(\overrightarrow a = \left( { - 2;1;2} \right)\), \(\overrightarrow b = \left( {1;1; - 1} \right)\).
a) Xác định tọa độ của \(\overrightarrow u = \overrightarrow a - 2\overrightarrow b \). (0,25 điểm)
b) Tính độ dài của \(\overrightarrow u \). (0,25 điểm)
c) Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\). (0,5 điểm)