 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Tập xác định: \(D = \mathbb{R}.\)
Ta có: \(y' = 3{x^2} - 4x + m - 1\).
Gọi \(M\left( {{x_0};{y_0}} \right) \in \left( C \right)\) là tiếp điểm.
Phương trình tiếp tuyến tại \(M\): \(y = k\left( {x - {x_0}} \right) + {y_0}.\)
Ta có: \(k = y'\left( {{x_0}} \right) = 3x_0^2 - 4{x_0} + m - 1\)
\(k' = 6{x_0} - 4\)
\(k' = 0 \Leftrightarrow {x_0} = \frac{2}{3} \Rightarrow k = \frac{{ - 7}}{3} + m.\)
Ta có bảng biến thiên sau:
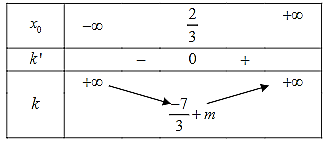
Từ đây, hệ số góc nhỏ nhất của tiếp tuyến của đồ thị \(\left( C \right)\) là \({k_{\min }} = \frac{{ - 7}}{3} + m\).
Tiếp tuyến này vuông góc với đường thẳng \(d:y = 3x + 2024\) khi và chỉ khi
\({k_{\min }} = \frac{{ - 1}}{{{k_d}}} = \frac{{ - 1}}{3}\) \( \Leftrightarrow \frac{{ - 7}}{3} + m = \frac{{ - 1}}{3} \Leftrightarrow m = 2.\)
Cho hàm số \(\left( C \right)\): \(y = \frac{{{x^2} - 3x + m}}{{x - 1}}.\)
a) Khảo sát và vẽ đồ thị hàm số \(\left( C \right)\) với \(m = - 4.\)
b) Với \(m = 2\), tính giá trị lớn nhất, giá trị nhỏ nhất của \(\left( C \right)\) trên đoạn \(\left[ {2;3} \right]\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
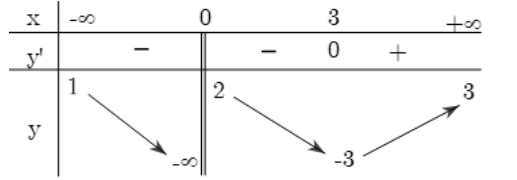
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
Cho hàm số \(y = f(x)\) liên tục và có đồ thị hàm số trên đoạn \(\left[ { - 2;4} \right]\) như hình vẽ dưới đây.
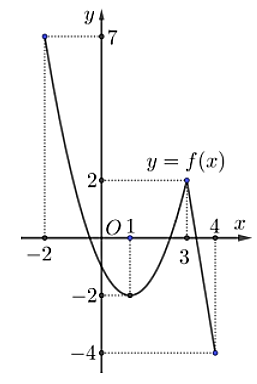
Tổng giá trị lớn nhất và nhỏ nhất của hàm số \(y = f(x)\) trên đoạn \(\left[ { - 2;4} \right]\) bằng:
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức sau:
\(G\left( x \right) = 0,025{x^2}\left( {30 - x} \right),\)
trong đó \(x\)là lượng thuốc được tiêm cho bệnh nhân (\(x\) được tính bằng miligam).
Liều lượng thuốc cần tiêm cho bệnh nhân nằm trong khoảng nào để huyết áp bệnh nhân tăng?
Hàm số \(y = f(x)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ dưới đây.
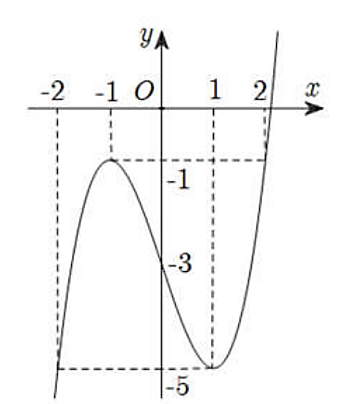
Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(y = f(x)\) trên đoạn \(\left[ { - 2;2} \right]\).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị trên đoạn \(\left[ { - 1;5} \right]\) như hình vẽ bên dưới.
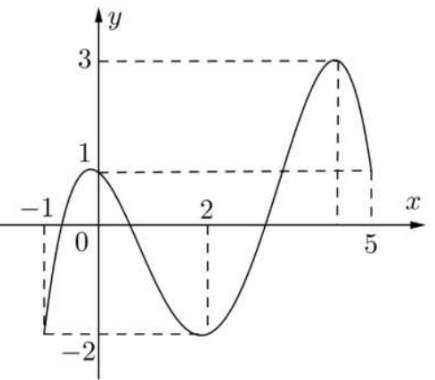
Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { - 1;5} \right]\) bằng: