 Giải bởi Vietjack
Giải bởi Vietjack
Gọi \(x\) là giá bán thực tế của mỗi quả bưởi Đoan Hùng \(\left( {30000 \le x \le 50000} \right)\), đơn vị: đồng.
Theo đề ta có:
Nếu bán với giá \(50000\) đồng thì bán được \(40\) quả bưởi
Giảm giá \(5000\) đồng thì bán được thêm \[50\] quả.
Giảm giá \(50000 - x\) thì bán được thêm bao nhiêu quả?
Khi đó, số quả bưởi được bán thêm là: \(\left( {50000 - x} \right)\frac{{50}}{{5000}} = \frac{1}{{100}}\left( {50000 - x} \right)\).
Do đó, số quả bưởi bán được tương ứng với giá bán \(x\):
\(40 + \frac{1}{{100}}\left( {50000 - x} \right) = \frac{{ - 1}}{{100}}x + 540\).
Gọi \(F\left( x \right)\) là hàm lợi nhuận thu được (\(F\left( x \right)\): đồng).
Ta có: \(F\left( x \right) = \left( {\frac{{ - 1}}{{100}}x + 540} \right)\left( {x - 30000} \right) = \frac{{ - 1}}{{100}}{x^2} + 840x - 16200000\).
Lúc này, bài toán trở thành tìm GTLN của hàm số:
\(F\left( x \right) = \frac{{ - 1}}{{100}}{x^2} + 840x - 16200000\) với \(30000 \le x \le 50000\).
\(F'\left( x \right) = \frac{{ - 1}}{{50}}x + 840\)
\(F'\left( x \right) = 0 \Leftrightarrow \frac{{ - 1}}{{50}}x + 840 = 0 \Leftrightarrow x = 42000\).
Vì hàm \(F\left( x \right)\) liên tục trên \(\left[ {30000;\,50000} \right]\) nên ta có:
\(F\left( {30000} \right) = 0\)
\(F\left( {42000} \right) = 1440000\)
\(F\left( {50000} \right) = 800000\).
Vậy với \(x = 42000\) thì \(F\left( x \right)\) đạt GTLN.
Vậy để cửa hàng thu được lợi nhuận lớn nhất thì giá bán thực tế của mỗi quả bưởi Đoan Hùng là \(42000\) đồng.
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
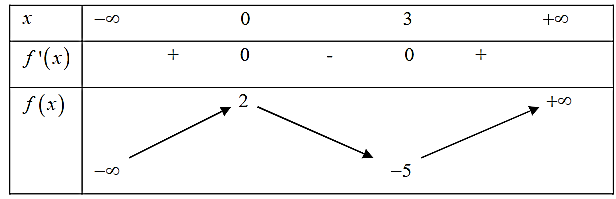
Giá trị cực tiểu của hàm số đã cho bằng:
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
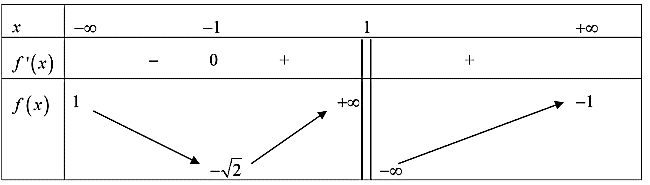
Tập hợp tất cả các giá trị thực của tham số \(m\) sao cho phương trình \(f\left( x \right) = m\) có ba nghiệm thực phân biệt.
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị trên đoạn \(\left[ { - 1;5} \right]\) như hình vẽ bên dưới.
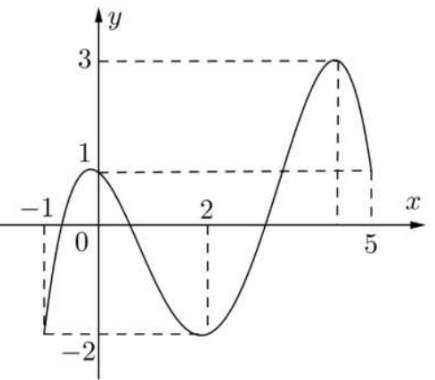
Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { - 1;5} \right]\) bằng:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
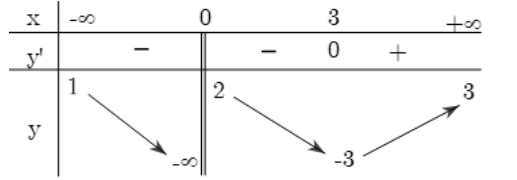
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
Cho hàm số \(\left( C \right)\): \(y = \frac{{{x^2} - 3x + m}}{{x - 1}}.\)
a) Khảo sát và vẽ đồ thị hàm số \(\left( C \right)\) với \(m = - 4.\)
b) Với \(m = 2\), tính giá trị lớn nhất, giá trị nhỏ nhất của \(\left( C \right)\) trên đoạn \(\left[ {2;3} \right]\).