PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ dưới đây.
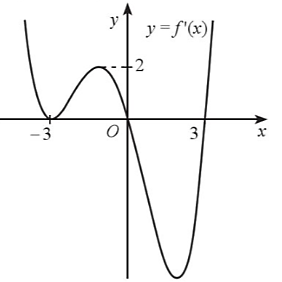
Xét hàm số \(g\left( x \right) = f\left( x \right) - x\). Hàm số \(g\left( x \right)\) có bao nhiêu điểm cực trị?
 Giải bởi Vietjack
Giải bởi Vietjack
Do hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) nên hàm số \(y = g\left( x \right)\) cũng xác định trên \(\mathbb{R}\).
Ta có \(g'\left( x \right) = f'\left( x \right) - 1\); \(g'\left( x \right) = 0\) khi \(f'\left( x \right) = 1\).
Số nghiệm của phương trình \(g'\left( x \right) = 0\) là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và đường thẳng \(y = 1\).
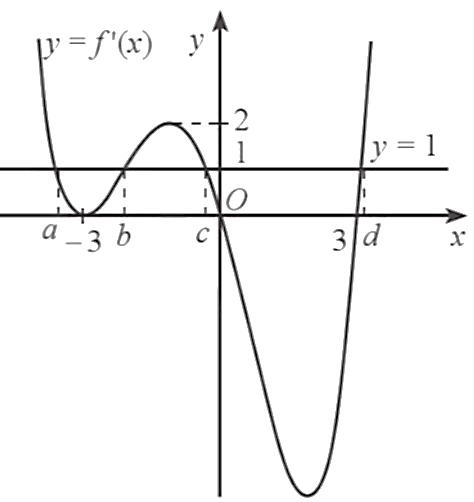
Căn cứ vào đồ thị hàm số, ta thấy phương trình \(f'\left( x \right) = 1\) hay \(g'\left( x \right) = 0\) có 4 nghiệm phân biệt. Gọi 4 nghiệm đó theo thứ tự từ bé đến lớn là \(a,\,b,\,c,\,d\).
Dựa vào vị trí của đồ thị hàm số \(y = f'\left( x \right)\) và đường thẳng \(y = 1\), ta có bảng xét dấu \(g'\left( x \right)\) như sau:

Vậy hàm số \(g\left( x \right) = f\left( x \right) - x\) có 4 điểm cực trị.
Đáp số: 4.
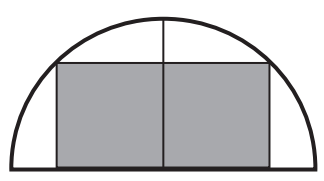
Ngân có một tấm giấy màu có dạng nửa hình tròn bán kính 8 cm. Ngân cần cắt từ tấm giấy màu này ra một tấm giấy hình chữ nhật có một cạnh thuộc đường kính của nửa hình tròn (xem hình dưới) sao cho diện tích của tấm bìa được cắt ra là lớn nhất. Giá trị lớn nhất của diện tích tấm bìa đó là bao nhiêu centimét vuông?
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình dưới đây.
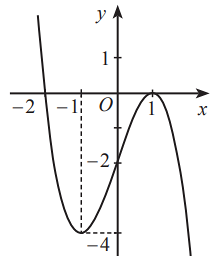
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng sau đây?
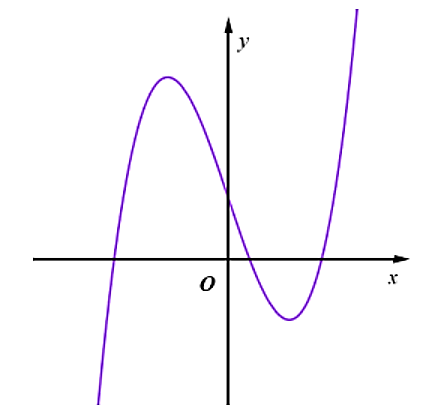
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình dưới?
Cho hình lăng trụ \(ABC.A'B'C'\) có hai đáy là các tam giác đều như hình dưới.
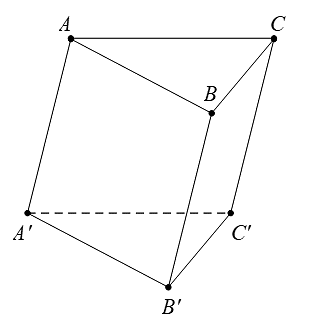
Góc giữa hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {A'C'} \) bằng
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\) và có bảng biến thiên như sau:
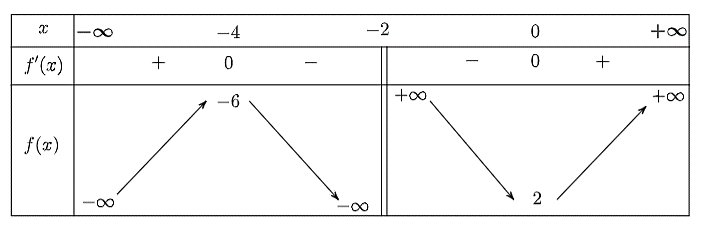
a) Hàm số \(y = f\left( x \right)\) đồng biến trên mỗi khoảng \[\left( { - \infty ; - 4} \right)\] và \(\left( {0;\, + \infty } \right)\).
b) Giá trị cực tiểu của hàm số đã cho là \({y_{CT}} = - 6\).
c) Hàm số \(y = f\left( x \right)\) có giá trị lớn nhất bằng \(2\) và giá trị nhỏ nhất bằng \( - 6\).
d) Công thức xác định hàm số là \(y = \frac{{{x^2} + 2x + 4}}{{x + 2}}\).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Khi đó:
a) \(\overrightarrow {A'D} = \overrightarrow {BC'} \).
b) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {DA} \).
c) \(\overrightarrow {C'A} = \overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {A'A} \).
d) Góc giữa hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {A'B'} \) bằng \(45^\circ \).
Cho hàm số \[y = f\left( x \right)\] xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) và có đồ thị như hình dưới đây.
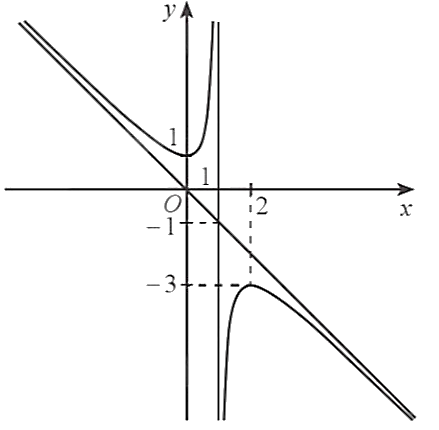
Phương trình đường tiệm cận đứng và phương trình đường tiệm cận xiên của đồ thị đã cho là
Xác định \(a,\,b,\,c\) để hàm số \(y = \frac{{ax - 1}}{{bx + c}}\) có đồ thị như hình vẽ dưới đây.
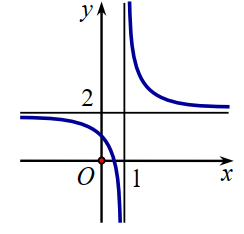
Chọn đáp án đúng.
Cho hình chóp tứ giác đều \(S.ABCD\) có độ dài tất cả các cạnh đều bằng \(a\). Đáy \(ABCD\) có tâm là \(O\). Khi đó:
a) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = 4\overrightarrow {SO} \).
b) \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
c) \(\left( {\overrightarrow {SA} ,\,\overrightarrow {AC} } \right) = 45^\circ \).
d) \(\overrightarrow {SA} \cdot \overrightarrow {AC} = - {a^2}\).
Cho hàm số \(y = \frac{{{x^2} - 2x - 3}}{{x - 2}}\).
a) Hàm số đã cho đồng biến trên mỗi khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
b) Hàm số đã cho có 2 cực trị.
c) Đồ thị hàm số nhận điểm \(I\left( {2;2} \right)\) là tâm đối xứng.
d) Có 5 điểm thuộc đồ thị hàm số có tọa độ nguyên.