Một chiếc đèn chùm treo có khối lượng \(m = 3\) kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích \(SA,\,SB,\,SC,\,SD\) sao cho \(S.ABCD\) là hình chóp tứ giác đều có \(\widehat {ASC} = 60^\circ \) như hình dưới.
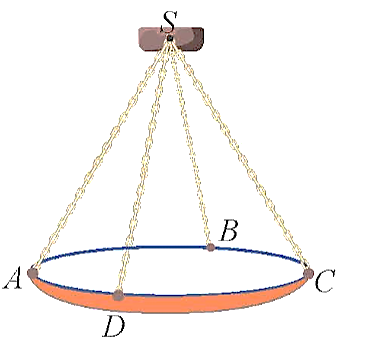
Độ lớn của lực căng cho mỗi sợi xích bằng bao nhiêu Newton (làm tròn kết quả đến hàng phần mười)? Biết rằng gia tốc rơi tự do có độ lớn 9,8 m/s2.
 Giải bởi Vietjack
Giải bởi Vietjack
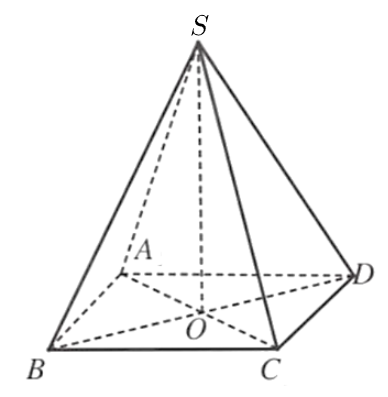
Gọi \(O\) là tâm của đáy \(ABCD\).
Vì \(S.ABCD\) là hình chóp tứ giác đều nên \(SO \bot \left( {ABCD} \right)\), \(SA = SB = SC = SD\) và \(O\) là trung điểm của \(AC\) và \(BD\).
Ta có: \(\widehat {ASC} = 60^\circ \), suy ra \(\widehat {ASO} = 30^\circ \).
Hợp lực của bốn sợi xích là:
\(\overrightarrow F = \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \left( {\overrightarrow {SA} + \overrightarrow {SC} } \right) + \left( {\overrightarrow {SB} + \overrightarrow {SD} } \right)\)\( = 2\overrightarrow {SO} + 2\overrightarrow {SO} = 4\overrightarrow {SO} \).
Để đèn chùm đứng yên thì hợp lực của các sợi xích phải cân bằng với trọng lực \(\overrightarrow P \), điều đó có nghĩa là \(4\overrightarrow {SO} = \overrightarrow P \), suy ra \(4\left| {\overrightarrow {SO} } \right| = \left| {\overrightarrow P } \right|\), hay \(SO = \frac{P}{4}\).
Độ lớn của trọng lực tác động lên đèn chùm là: \(P = mg = 3 \cdot 9,8 = 29,4\) (N).
Do đó, \(SO = \frac{{29,4}}{4} = 7,35\).
Ta có: \(SA = \frac{{SO}}{{\cos \widehat {ASO}}} = \frac{{7,35}}{{\cos 30^\circ }} = \frac{{49\sqrt 3 }}{{10}} \approx 8,5\).
Vậy độ lớn của lực căng cho mỗi sợi xích bằng khoảng 8,5 N.
Đáp số: \(8,5\).
Người ta kéo vật nặng bằng một lực \(\overrightarrow F \) có cường độ \(200\) N như hình dưới đây.
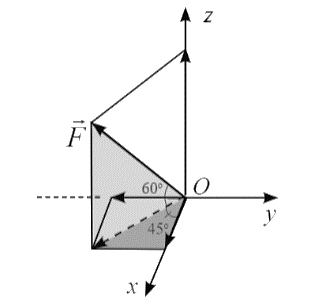
Khi đó, ta biểu diễn được tọa độ của vectơ \(\overrightarrow F \) trong hệ tọa độ trên là \(\overrightarrow F = \left( {a\sqrt 2 ; - b\sqrt 2 ;c\sqrt 3 } \right)\) (với \(a,b,c \in \mathbb{Z}\)). Giá trị của biểu thức \(K = a - 2b + c\) bằng bao nhiêu?
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = {x^3} - 3{x^2} + \left( {m + 1} \right)x + 2\) có hai điểm cực trị?
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
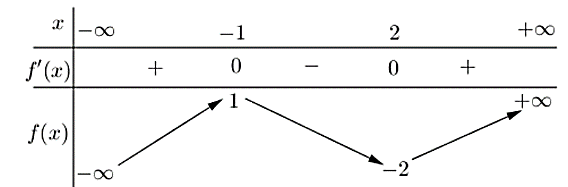
Hàm số đã cho đạt cực đại tại
Cho hàm số \[y = f\left( x \right)\] liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị hàm số như hình vẽ dưới đây.
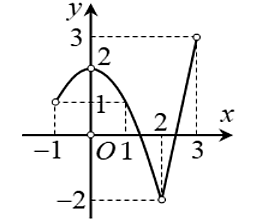
Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ {0;\,2} \right]\) bằng bao nhiêu?
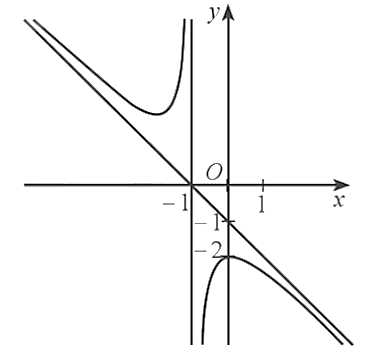
Đường cong trong hình dưới đây là đồ thị của hàm số nào trong các hàm số ở các phương án sau:
Trong không gian với hệ tọa độ \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\) có \(A'\left( {1;\,0 & ;\,1} \right)\), \(B'\left( {3;1;\,3} \right)\), \(D'\left( {1;\, - 1;1} \right)\), \(C\left( {3;\,5;\, - 5} \right)\).
a) Tọa độ của vectơ \(\overrightarrow {A'D'} \) là \(\left( {0; - 1;0} \right)\).
b) Gọi tọa độ của điểm \(B\) là \(\left( {{x_B};\,{y_B};{z_B}} \right)\), ta có tọa độ của vectơ \(\overrightarrow {BC} \) là:
\(\left( {{x_B} - 3;{y_B} - 5;{z_B} + 5} \right)\).
c) Tọa độ của điểm \(B\) là \(\left( {3;6; - 5} \right)\).
d) Tọa độ của vectơ tổng \(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {DD'} \) là \(\left( { - 2;\, - 7;6} \right)\).
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ dưới đây.
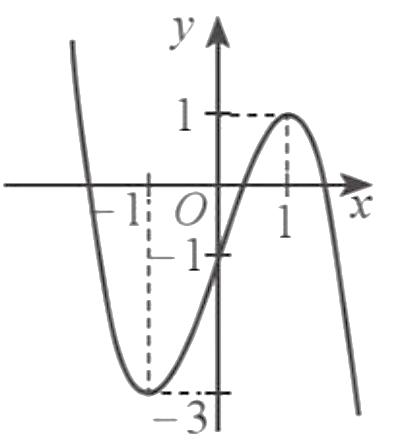
Phát biểu nào sau đây là đúng?
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ dưới đây.
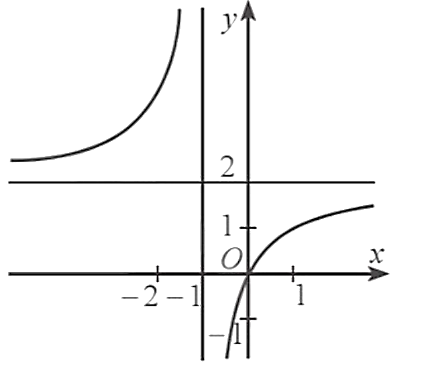
Phát biểu nào dưới đây là đúng?
Cho hàm số \(y = \frac{{x - 3}}{{x + 1}}\).
a) Hàm số đã cho đồng biến trên \[\mathbb{R}\backslash \left\{ { - 1} \right\}\].
b) Hàm số đã cho đạt cực đại tại \(x = 4\).
c) Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng \(x = - 1\), tiệm cận ngang là đường thẳng \(y = 1\).
d) Có \(2\,023\) giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2\,024;2\,024} \right]\) để đường thẳng \(y = x + 2m\) cắt đồ thị hàm số đã cho tại hai điểm nằm về hai phía của trục tung.