Cho hàm số \[y = \frac{{ax - b}}{{x - 1}}\] có đồ thị như hình vẽ dưới đây:
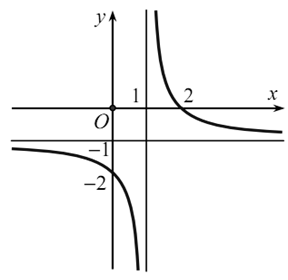
Khẳng định nào sau đây đúng?
A. \(b < a < 0\).
B. \(a < b < 0\).
C. \(b > a\)và \(a < 0\).
D. \(a < 0 < b\).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Tiệm cận ngang của đồ thị hàm số là \[y = \frac{a}{1} = - 1 \Rightarrow a = - 1\].
Giao điểm của đồ thị hàm số với Oy là \(\left( {0\,;\,b} \right) \equiv \left( {0\,;\, - 2} \right) \Rightarrow b = - 2\).
Vậy \(b < a < 0\).
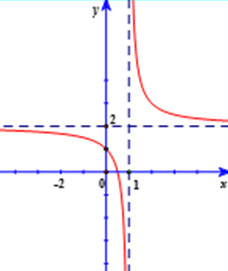
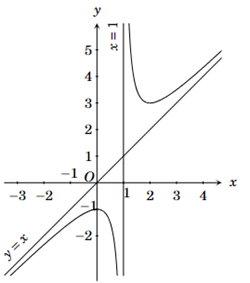
Xác định \(a,\,b,\,c\) để hàm số \(y = \frac{{ax - 1}}{{bx + c}}\) có đồ thị như hình vẽ bên. Chọn đáp án đúng?
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ bên dưới.
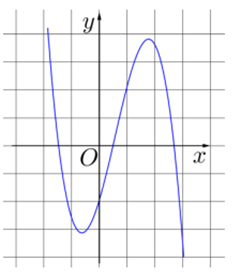
Mệnh đề nào dưới đây đúng?
Tọa độ điểm M thuộc đồ thị (C) của hàm số \(y = \frac{{2x - 1}}{{x - 1}}\) sao cho khoảng cách từ điểm M đến tiệm cận đứng bằng 1 là
I. Nhận biết
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
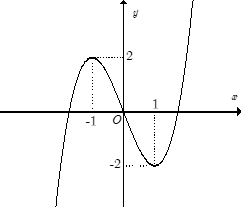
II. Thông hiểu
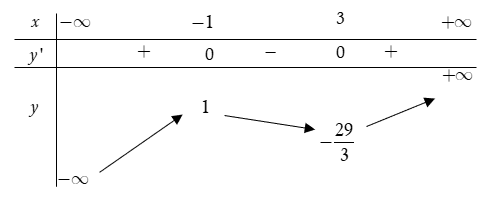
Cho hàm số y = f(x) = ax3 + bx2 + cx + d có bảng biến thiên sau:
Đồ thị nào trong các phương án A, B, C, D thể hiện hàm số y = f(x)?
Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên như sau?
Biết rằng hàm số y = f(x) = ax3 + bx2 + cx + d (a ≠ 0) có đồ thị là một trong các dạng dưới đây:
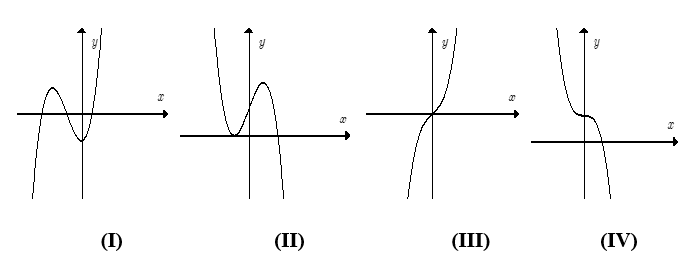
Mệnh đề nào sau đây là đúng?
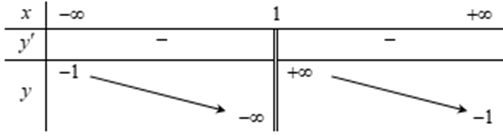
Hàm số \(y = \frac{{3x + 2}}{{x - 1}}\) có bảng biến thiên nào dưới đây. Chọn đáp án đúng?
Bảng biến thiên trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?