I. Nhận biết
Cho đồ thị hàm số bậc ba \[f(x) = a{x^3} + b{x^2} + cx + d\] có bảng xét dấu như hình vẽ bên dưới.
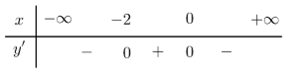
Hàm số đã cho đồng biến trên khoảng nào sau đây?
A. \[(0; + \infty ).\]
B. \[( - \infty ; - 2).\]
C. \[( - 3;1).\]
D. \[( - 2;0).\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Dựa vào bảng xét dấu, ta có hàm số đồng biến trên khoảng \[( - 2;0).\]
Cho đồ thị hàm số bậc ba \[f(x) = a{x^3} + b{x^2} + cx + d\] \[(a \ne 0,{\rm{ }}a,{\rm{ }}b,{\rm{ }}c,{\rm{ }}d \in \mathbb{R})\] có bảng biến thiên như hình vẽ bên dưới.
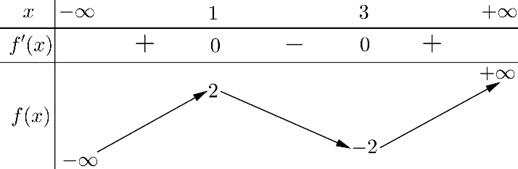
Hàm số đã cho đồng biến trên khoảng nào sau đây?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ sau
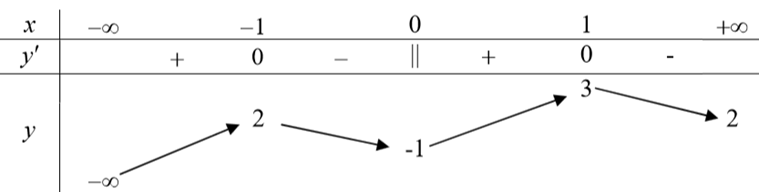
Mệnh đề nào dưới đây đúng?
III. Vận dụng
Cho hàm số \(y = f(x)\). Hàm số \(y = f'(x)\) có đồ thị như hình vẽ:
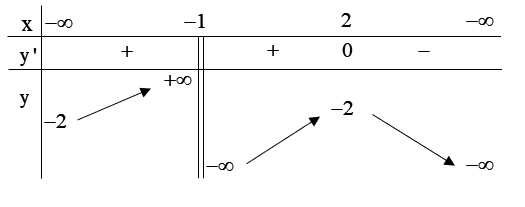
Khẳng định nào sau đây là khẳng định đúng?
Số giá trị \[m\] nguyên để hàm số \(y = \frac{{mx + 2}}{{x + m}}\) nghịch biến trên từng khoảng xác định của nó là
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau
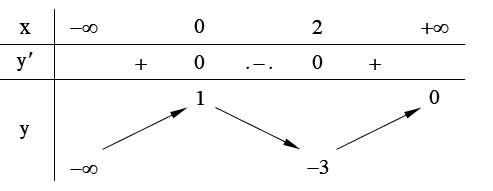
Giá trị cực đại của hàm số \(y = f\left( x \right)\) bằng
II. Thông hiểu
Cho hàm số \[y = {x^3} + 3{x^2} - 9x + 15\]. Khẳng định nào sau đây là khẳng định sai?
Cho hàm số \(y = {x^2}\left( {3 - x} \right)\). Mệnh đề nào sau đây là đúng?
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 4x - 1\) có bao nhiêu điểm cực trị ?
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
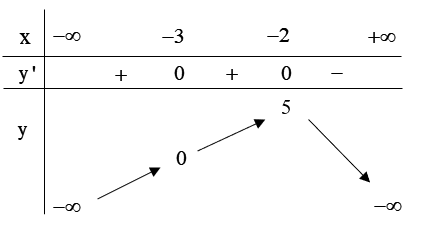
Trong các mệnh đề sau, có bao nhiêu mệnh đề sai?
I. Hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ; - 5} \right)\) và \(\left( { - 3; - 2} \right)\).
II. Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;5} \right)\).
III. Hàm số đã cho nghịch biến trên khoảng \(\left( { - 2; + \infty } \right)\).
IV. Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
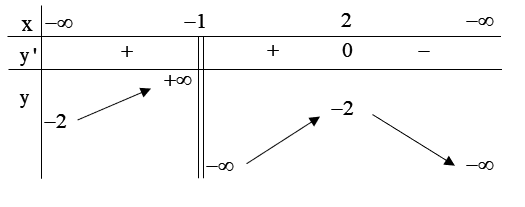
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
Cho hàm số \[f(x)\] có bảng biến thiên:
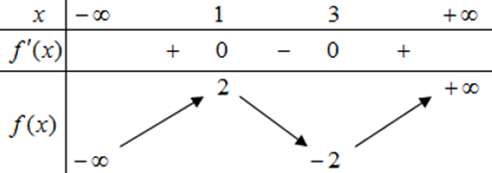
Hàm số đã cho đạt cực tiểu tại điểm nào sau đây ?