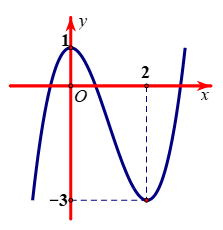
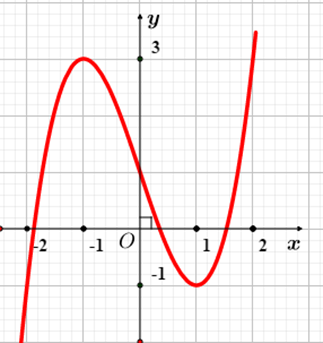
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong như hình vẽ. Hàm số đạt cực đại tại điểm nào dưới đây?
A. \(x = - 3\).
B. \(x = 1\).
C. \(x = 0\).
D. \(x = 2\).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Từ đồ thị hàm số ta có hàm số đạt cực đại tại \(x = 0\).
Sau khi phát hiện một dịch bệnh, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là f(t) = 45t2 – t3, t = 0, 1, 2, …, 25. Nếu coi f(t) là hàm số xác định trên đoạn [0; 25] thì đạo hàm f'(t) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Xác định khoảng thời gian mà tốc độ truyền bệnh giảm?
III. Vận dụng
Cho hàm số \(y = f(x)\). Hàm số \(y = f'(x)\) có đồ thị như hình vẽ:
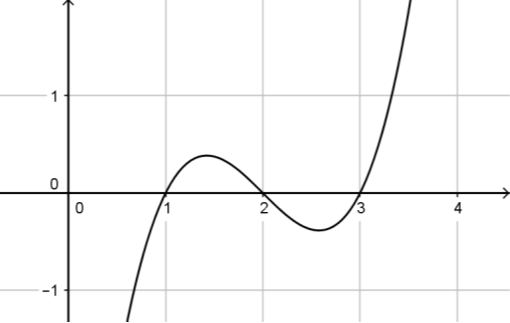
Khẳng định nào sau đây là khẳng định đúng?
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
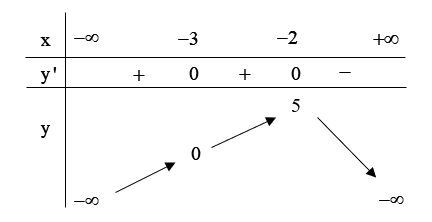
Trong các mệnh đề sau, có bao nhiêu mệnh đề sai?
I. Hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ; - 5} \right)\) và \(\left( { - 3; - 2} \right)\).
II. Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;5} \right)\).
III. Hàm số đã cho nghịch biến trên khoảng \(\left( { - 2; + \infty } \right)\).
IV. Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
II. Thông hiểu
Cho hàm số \[y = {x^3} + 3{x^2} - 9x + 15\]. Khẳng định nào sau đây là khẳng định sai?
I. Nhận biết
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào?
Hàm số\[y = - {x^3} + 3{x^2} + 1\] nghịch biến khi \[x\] thuộc khoảng nào sau đây?
Một chuyển động thẳng xác định bởi phương trình \(s = \frac{1}{3}{t^3} - 3{t^2} + 5t + 2\) với \(t \ge 0\), trong đó t tính bằng giây và s tính bằng mét. Trong khoảng thời gian nào vận tốc của vật tăng?
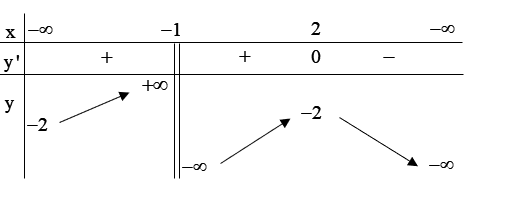
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ sau
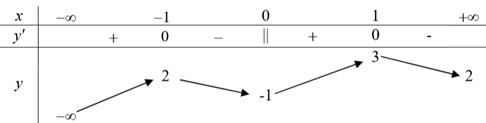
Mệnh đề nào dưới đây đúng?
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau
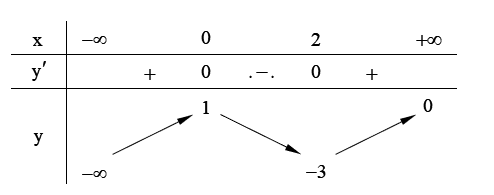
Giá trị cực đại của hàm số \(y = f\left( x \right)\) bằng
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 4x - 1\) có bao nhiêu điểm cực trị ?
Cho hàm số \[y = {x^3} - 3{x^2} - 2\]. Gọi \[a,b\]lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số đó. Giá trị của \[2{a^2} + b\] là:
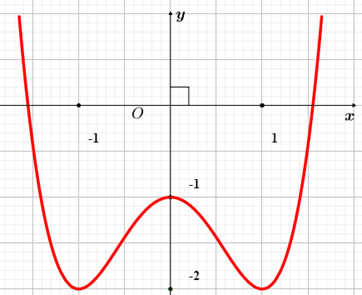
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?