II. Thông hiểu
Giá trị của \[x\] để biểu thức \(\frac{x}{{x - 2}} + \sqrt {2 - x} \) có nghĩa là
A. \(x \ge 2\).
B. \(x > 2\).
C. \(x \le 2\).
D. \(x < 2\).
Giải bởi Vietjack
Đáp án đúng là: D
Biểu thức \(\frac{x}{{x - 2}} + \sqrt {2 - x} \) có nghĩa khi và chỉ khi \(x - 2 \ne 0\) và \(2 - x \ge 0\).
Ta có:
⦁ \(x - 2 \ne 0\) khi \(x \ne 2\);
⦁ \(2 - x \ge 0\) khi \(x \le 2.\)
Như vậy, biểu thức \(\frac{x}{{x - 2}} + \sqrt {2 - x} \) xác định khi \(x < 2.\)
Ta chọn phương án D.
III. Vận dụng
Để lái xe an toàn khi qua đoạn đường có dạng cung tròn, người lái xe cần biết tốc độ tối đa cho phép là bao nhiêu. Vì thế, ở những đoạn đường đó thường có bảng chỉ dẫn cho tốc độ tối đa cho phép của ô tô. Tốc độ tối đa cho phép \(v\) (m/s) được tính bởi công thức \(v = \sqrt {rg\mu } ,\) trong đó \(r\) (m) là bán kính của cung đường, \(g = 9,8\) m/s2, \(\mu \) là hệ số ma sát trượt của đường. Tốc độ tối đa cho phép để lái xe an toàn khi đi qua đoạn đường có dạng cung tròn với bán kính \(r = 300\) m (làm tròn kết quả đến hàng phần mười), biết \(\mu = 0,12\) là
I. Nhận biết
Biểu thức nào sau đây không phải là căn thức bậc hai?
Có hai xã cùng ở một bên bờ sông. Người ta đo được khoảng cách từ trung tâm \[A,{\rm{ }}B\] của hai xã đó đến bờ sông lần lượt là \[AA' = 600{\rm{\;m}},{\rm{ }}BB' = 700{\rm{\;m}}\]và khoảng cách \[A'B' = 2{\rm{ }}500{\rm{\;m}}\] (hình vẽ).
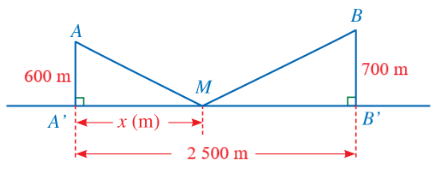
Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông cho người dân hai xã. Giả sử vị trí của trạm cung cấp nước sạch đó là điểm \[M\] trên đoạn \[A'B'\] với Khẳng định nào sau đây là đúng?
Công thức \(h = 0,4 \cdot \sqrt[3]{x}\) biểu diễn mối liên hệ giữa cân nặng \(x\) (kg) và chiều cao \(h\) (m) của một con hươu cao cổ ở tuổi trưởng thành (Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017). Một con hươu cao cổ có chiều cao là \(2,68\) m thì nặng bao nhiêu kilôgam (làm tròn kết quả đến hàng đơn vị)?
Với \(x = 2\), biểu thức \(A = 5\sqrt {3x} - \sqrt {12x} + \sqrt {75x} - 15\) có giá trị bằng \(a\sqrt 6 + b.\) Khi đó, tổng bình phương của \(a\) và \(b\) bằng
Giá trị biểu thức \(\sqrt {\frac{{1 - 2x}}{{{x^2}}}} \) khi \(x = - 2\) là
Giá trị của biểu thức \(\sqrt[3]{{{x^2} + 4}} - \sqrt {2 - x} \) tại \(x = - 2\) là
Điều kiện xác định của biểu thức \(\sqrt {3 - x} + \sqrt[3]{{\frac{1}{{9 - {x^2}}}}}\) là
Giá trị của biểu thức \(\sqrt {{{\left( {a - \sqrt 3 } \right)}^2}} + \sqrt 2 \) khi \(a = \sqrt 2 \) là
