Từ một tấm thép hình vuông, người thợ cắt ra hai mảnh hình chữ nhật có diện tích lần lượt là \[24{\rm{ c}}{{\rm{m}}^{\rm{2}}}\] và \[40{\rm{ c}}{{\rm{m}}^{\rm{2}}}\] như hình vẽ.
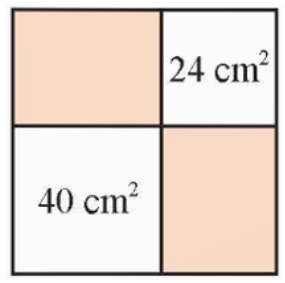
Diện tích phần còn lại của tấm thép là
A. \(10\sqrt {15} \,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\)
B. \(12\sqrt {15} \,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\)
C. \(4\sqrt {15} \,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\)
D. \(16\sqrt {15} \,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\)
Giải bởi Vietjack
Đáp án đúng là: D
Cạnh của hình vuông có diện tích \[24{\rm{ c}}{{\rm{m}}^{\rm{2}}}\] là:
\(\sqrt {24} = \sqrt {4 \cdot 6} = \sqrt 4 \cdot \sqrt 6 = 2\sqrt 6 {\rm{\;(cm)}}{\rm{.}}\)
Cạnh của hình vuông có diện tích \[40{\rm{ c}}{{\rm{m}}^{\rm{2}}}\] là:
\[\sqrt {40} = \sqrt {4 \cdot 10} = \sqrt 4 \cdot \sqrt {10} = 2\sqrt {10} {\rm{\;(cm)}}{\rm{.}}\]
Hai hình chữ nhật còn lại có chiều dài bằng nhau (đều bằng cạnh của hình vuông có diện tích \[40{\rm{ c}}{{\rm{m}}^{\rm{2}}})\] và có chiều rộng bằng nhau (đều bằng cạnh của hình vuông có diện tích \[24{\rm{ c}}{{\rm{m}}^{\rm{2}}}).\]
Diện tích phần còn lại của tấm thép (bằng tổng diện tích hai hình chữ nhật trong hình vẽ) là:
\(2 \cdot \left( {2\sqrt 6 \cdot 2\sqrt {10} } \right) = 8\sqrt {6 \cdot 10} = 8\sqrt {60} = 8\sqrt {4 \cdot 15} = 8 \cdot 2 \cdot \sqrt {15} = 16\sqrt {15} {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Vậy diện tích phần còn lại của tấm thép là \(16\sqrt {15} \,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\)
Chiều cao ngang vai của một con voi đực ở Châu Phi là \[h{\rm{\;(cm)}}\] có thể được tính xấp xỉ bằng công thức: \(h = 62,5\sqrt[3]{t} + 75,8\) với \[t\] là tuổi của con voi tính theo năm. Một con voi đực 8 tuổi ở Châu Phi sẽ có chiều cao ngang vai xấp xỉ là
III. Vận dụng
Hệ quả của hiện tượng nóng lên toàn cầu là băng của một số sông băng đang tan chảy. Mười hai năm sau khi băng biến mất, những loài thực vật nhỏ bé, được gọi là địa y, bắt đầu mọc trên đá. Mỗi nhóm địa y phát triển ở dạng (gần như) một hình tròn. Đường kính \[d{\rm{\;(mm)}}\] của hình tròn này có thể được tính gần đúng bằng công thức: \(d = 7\sqrt {t - 12} \) với \[t\] là số năm tính từ khi băng biến mất \[\left( {t \ge 12} \right).\] Đường kính của hình tròn do địa y tạo nên sau khi băng biến mất 13 năm và 16 năm lần lượt là
I. Nhận biết
Căn bậc hai của một số \(a\) không âm là một số \(x\) sao cho
Rút gọn biểu thức \(\frac{x}{y}:\sqrt {\frac{{{x^2}}}{{{y^4}}}} \) với \(x > 0\,,\,\,y \ne 0\) ta được
Với \(m = 2\), giá trị của biểu thức \(\sqrt {\frac{m}{{75}}} \cdot \sqrt {\frac{{121}}{{16m}}} \cdot \sqrt {\frac{3}{{64}}} \) bằng
II. Thông hiểu
Giá trị của \[x\] để căn thức \[\frac{3}{{\sqrt { - {x^2} - 2} }}\] có nghĩa là
Rút gọn biểu thức \(\left( {\frac{3}{{\sqrt {1 + a} }} + \sqrt {1 - a} } \right):\left( {\frac{3}{{\sqrt {1 - {a^2}} }} + 1} \right)\) với \( - 1 < a < 1\) ta được
</>
Điều kiện xác định của biểu thức \(\frac{{x + 3}}{{\sqrt {2 - x} }}\) là
Một hình lập phương có thể tích bằng \[729{\rm{ c}}{{\rm{m}}^{\rm{3}}}\]. Độ dài cạnh của hình lập phương đó là
Giá trị biểu thức \(\sqrt[3]{{64}} \cdot \sqrt[3]{{125}} - \sqrt[3]{{216}}\) bằng
