Cho hai đường tròn \[\left( {O;4{\rm{\;cm}}} \right)\] và \[\left( {O';3{\rm{\;cm}}} \right)\] biết \[OO' = 5{\rm{\;cm}}.\] Hai đường tròn trên cắt nhau tại \[A\] và \[B.\] Độ dài \[AB\] là
A. \[5{\rm{\;cm}}.\]
Giải bởi Vietjack
Đáp án đúng là: C
Gọi \[H\] là giao điểm của \[OO'\] và \[AB.\]
Vì \[{4^2} + {3^2} = {5^2}\] hay \(O{A^2} + O'{A^2} = O{O'^2}\) nên theo định lí Pythagore đảo, ta được tam giác \[OO'A\] vuông tại \[A.\]
Vì \[OA = OB = 4{\rm{\;(cm)}}\] nên \[O\] nằm trên đường trung trực của đoạn \[AB.\]
Chứng minh tương tự, ta được \[O'\] nằm trên đường trung trực của đoạn \[AB.\]
Khi đó \[OO'\] là đường trung trực của đoạn \[AB.\]
Vì vậy \[OO' \bot AB\] tại \[H\] và \[H\] là trung điểm \[AB.\]
Xét \[\Delta OAH\] và \[\Delta OO'A,\] có: \[\widehat {OHA} = \widehat {OAO'} = 90^\circ \] và \[\widehat {AOH}\] là góc chung.
Do đó (g.g)
Suy ra \[\frac{{AH}}{{O'A}} = \frac{{OA}}{{OO'}}\] nên \[AH = \frac{{OA}}{{OO'}} \cdot O'A = \frac{4}{5} \cdot 3 = \frac{{12}}{5}{\rm{\;(cm)}}{\rm{.}}\]
Vì \[H\] là trung điểm 
nên \[AB = 2AH = 2 \cdot \frac{{12}}{5} = \frac{{24}}{5} = 4,8{\rm{\;(cm)}}{\rm{.}}\]
Vậy ta chọn phương án C.
Cho hai đường tròn \(\left( O \right)\) đường kính \(7{\rm{\;cm}}\) và \(\left( {I;\,4{\rm{\;cm}}} \right).\) Biết \(OI = 1{\rm{\;cm,}}\) vị trí tương đối của hai đường tròn \(\left( O \right)\) và \(\left( I \right)\) là
II. Thông hiểu
Cho hình chữ nhật \[ABCD\] có \[AC = 16{\rm{\;cm}}.\] Biết rằng bốn điểm \[A,B,C,D\] cùng thuộc một đường tròn. Gọi \[O\] là giao điểm của hai đường chéo \[AC\] và \[BD.\] Tâm và bán kính của đường tròn đó là
Cho hai đường tròn \(\left( {O;1{\rm{\;cm}}} \right)\) và \(\left( {I;3{\rm{\;cm}}} \right)\) cắt nhau, đoạn thẳng \(OI\) có độ dài là
Trong một trò chơi, hai bạn Thủy và Tiến cùng chạy trên một đường tròn tâm \[O\] có bán kính \[20{\rm{\;m}}\] (hình vẽ).
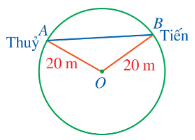
Độ dài dây \[AB\] nối vị trí của hai bạn đó không thể bằng bao nhiêu mét?
Cho hai đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và \(\left( {I;R} \right)\) với \(R < 5{\rm{\;cm}}.\) Biết \(OI = 3{\rm{\;cm}},\) giá trị của \(R\) để hai đường tròn tiếp xúc trong là
Cho đường tròn \(\left( {I;R} \right)\) có đường kính \[12{\rm{\;dm}}\] và đường tròn \(\left( {J;R'} \right)\) có đường kính \[18{\rm{\;dm}}.\] Nếu \(IJ = 15{\rm{\;dm}}\) thì hai đường tròn \[\left( I \right),\,\,\left( J \right)\] có vị trí tương đối là
Cho hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] với \[R > r\] cắt nhau tại hai điểm phân biệt và \[OO' = d.\] Chọn khẳng định đúng?
Cho đường tròn \[\left( O \right)\] có bán kính \[R = 5{\rm{\;cm}}.\] Khoảng cách từ tâm đến dây \[AB\] là \[3{\rm{\;cm}}.\] Độ dài dây \[AB\] bằng
Cho hai đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và \(\left( {I;R} \right)\). Biết \(OI = 7{\rm{\;cm}},\) giá trị của \(R\) để hai đường tròn ở ngoài nhau là
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn?
Cho đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và một điểm \[K\] bất kì. Biết rằng \[OK = 7{\rm{\;cm}}.\] Khẳng định nào sau đây đúng?
Cho đường tròn \[\left( O \right)\] đường kính \[AB\] và dây \[CD\] không đi qua tâm. Khẳng định nào sau đây là đúng?
III. Vận dụng
Cho đường tròn \[\left( {O;R} \right)\] có hai dây \[AB,CD\] vuông góc với nhau tại \[M.\] Giả sử \[AB = 16{\rm{\;cm}},CD = 12{\rm{\;cm}},MC = 2{\rm{\;cm}}.\] Kẻ \[OH \bot AB\] tại \[H,\] \[OK \bot CD\] tại \[K.\] Khi đó diện tích tứ giác \[OHMK\] bằng
