Cho đường tròn \[\left( O \right)\] và hai điểm \[A,B\] nằm trên đường tròn \[\left( O \right).\] Nếu hai tiếp tuyến của đường tròn \[\left( O \right)\] tại \[A,B\] cắt nhau tại \[M\] thì
A. \[MO\] là tia phân giác của \[\widehat {OAM}.\]
B. \[MO\] là tia phân giác của \[\widehat {BOM}.\]
C. \[MO\] là tia phân giác của \[\widehat {AOM}.\]
D. \[MO\] là tia phân giác của \[\widehat {AMB.}\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
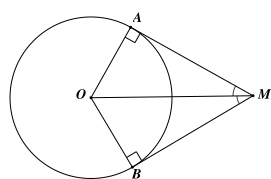
Cho đường tròn \[\left( O \right)\] và hai điểm \[A,B\] nằm trên đường tròn \[\left( O \right).\] Nếu hai tiếp tuyến của đường tròn \[\left( O \right)\] tại \[A,B\] cắt nhau tại \[M\] thì \[MO\] là tia phân giác của \[\widehat {AMB.}\]
Vậy ta chọn phương án D.
Cho điểm \[M\] nằm ngoài đường tròn \[\left( I \right)\] và \[ME,MF\] là hai tiếp tuyến của đường tròn này tại \[E,F.\] Cho biết \[\widehat {EMF} = 60^\circ .\] Tam giác \[EMF\] là tam giác gì?
II. Thông hiểu
Cho hình vẽ dưới đây biết \(AB,\,\,CB\) là hai tiếp tuyến của đường tròn \(\left( D \right).\)
![Cho hình vẽ dưới đây biết A B , C B là hai tiếp tuyến của đường tròn ( D ) .Giá trị của \[x\] bằng (ảnh 1)](https://video.vietjack.com/upload2/images/1731473440/1731474154-image5.png)
Giá trị của \[x\] bằng
I. Nhận biết
Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Kết luận nào sau đây là đúng?
Một thủy thủ đang ở trên cột buồm của một con tàu, cách mặt nước biển \[10{\rm{\;m}}.\] Biết bán kính Trái Đất là khoảng \[6\,\,400{\rm{\;km}}.\] Tầm nhìn xa tối đa (làm tròn kết quả đến hàng phần nghìn của km) của thủy thủ đó bằng khoảng
III. Vận dụng
Cho nửa đường tròn \[\left( {O;R} \right)\] đường kính \[AB.\] Vẽ các tia tiếp tuyến \[Ax,By\] với nửa đường tròn. Lấy điểm \[M\] di động trên tia \[Ax,\] điểm \[N\] di động trên tia \[By\] sao cho \[AM \cdot BN = {R^2}.\] Cho các nhận định sau:
(i) \[MN\] là tiếp tuyến của đường tròn \[\left( O \right).\]
(ii) \[\widehat {MON} = 90^\circ .\]
Kết luận nào sau đây là đúng nhất?
Cho đường tròn \[\left( I \right)\] và hai điểm \[P,Q\] thuộc đường tròn \[\left( I \right).\] Nếu hai tiếp tuyến của đường tròn \[\left( I \right)\] tại \[P,Q\] cắt nhau tại \[E\] thì
Hai tiếp tuyến tại \[B\] và \[C\] của đường tròn \[\left( {O;R} \right)\] cắt nhau tại \[A.\] Vẽ đường kính \[CD\] đường tròn \[\left( O \right).\] Khẳng định nào sau đây là đúng?
Cho đường tròn \[\left( O \right)\] đường kính \[AD.\] Vẽ tiếp tuyến \[AC\] tại \[A\] của đường tròn, từ \[C\] trên tiếp tuyến đó vẽ tiếp tuyến thứ hai \[CM\] của đường tròn \[\left( O \right)\] (\[M\] là tiếp điểm và \[M\] khác \[A\]) cắt \[AD\] tại \[B.\] Giả sử \[AC = 6{\rm{\;cm}},AB = 8{\rm{\;cm}}.\] Độ dài \[BM\] bằng
Hai tiếp tuyến tại \[A\] và \[B\] của đường tròn \[\left( O \right)\] cắt nhau tại \[I.\] Đường thẳng qua \[I\] vuông góc với \[IA\] cắt \[OB\] tại \[K.\] Khẳng định nào sau đây là đúng?
Cho đường tròn \[\left( O \right),\] từ một điểm \[M\] ở ngoài \[\left( O \right),\] vẽ hai tiếp tuyến \[MA\] và \[MB\] sao cho \[\widehat {AMB}\] bằng \[120^\circ .\] Biết chu vi tam giác \[MAB\] là \[6\left( {3 + 2\sqrt 3 } \right){\rm{\;cm}}.\] Khi đó độ dài dây \[AB\] bằng
Cho đường tròn \[\left( O \right)\] và hai điểm \[M,N\] thuộc đường tròn \[\left( O \right).\] Nếu hai tiếp tuyến của đường tròn \[\left( O \right)\] tại \[M,N\] cắt nhau tại \[A\] thì
Hai tiếp tuyến tại \[B\] và \[C\] của đường tròn \[\left( {O;R} \right)\] cắt nhau tại \[A.\] Khẳng định nào sau đây là sai?
Cho đường tròn \[\left( {O;R} \right)\] đường kính \[BC,\] lấy điểm \[A \in \left( O \right).\] Gọi \[H\] là trung điểm của \[AC.\] Tia \[OH\] cắt đường tròn \[\left( O \right)\] tại \[M.\] Từ \[A\] vẽ tiếp tuyến với đường tròn \[\left( O \right)\] cắt tia \[OM\] tại \[N.\] Cho các khẳng định sau:
(i) \[OH \cdot ON = {R^2}.\]
(ii) \[CN\] là tiếp tuyến của \[\left( O \right).\]
Kết luận nào sau đây là đúng nhất?
Cho đường tròn \[\left( O \right)\] và điểm \[A\] nằm trên đường tròn \[\left( O \right).\] Nếu đường thẳng \[d \bot OA\] tại \[A\] thì