15 câu trắc nghiệm Toán 9 Cánh diều Bài 3. Tiếp tuyến của đường tròn có đáp án
-
153 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Kết luận nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì điểm đó cách đều hai tiếp điểm.
Vậy ta chọn phương án B.
Câu 2:
Cho đường tròn \[\left( O \right)\] và điểm \[A\] nằm trên đường tròn \[\left( O \right).\] Nếu đường thẳng \[d \bot OA\] tại \[A\] thì
 Xem đáp án
Xem đáp án
Đáp án đúng là: A

Vì đường thẳng \[d\] đi qua điểm \[A\] nằm trên đường tròn \[\left( O \right)\] và vuông góc với bán kính \[OA\] của đường tròn \[\left( O \right)\] nên đường thẳng \[d\] là một tiếp tuyến của đường tròn \[\left( O \right).\]
Tức là, \[d\] là tiếp tuyến của \[\left( O \right),\] với \[A\] là tiếp điểm.
Vậy ta chọn phương án A.
Câu 3:
Cho đường tròn \[\left( O \right)\] và hai điểm \[A,B\] nằm trên đường tròn \[\left( O \right).\] Nếu hai tiếp tuyến của đường tròn \[\left( O \right)\] tại \[A,B\] cắt nhau tại \[M\] thì
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
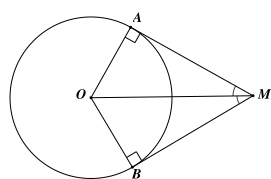
Cho đường tròn \[\left( O \right)\] và hai điểm \[A,B\] nằm trên đường tròn \[\left( O \right).\] Nếu hai tiếp tuyến của đường tròn \[\left( O \right)\] tại \[A,B\] cắt nhau tại \[M\] thì \[MO\] là tia phân giác của \[\widehat {AMB.}\]
Vậy ta chọn phương án D.
Câu 4:
Cho đường tròn \[\left( O \right)\] và hai điểm \[M,N\] thuộc đường tròn \[\left( O \right).\] Nếu hai tiếp tuyến của đường tròn \[\left( O \right)\] tại \[M,N\] cắt nhau tại \[A\] thì
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
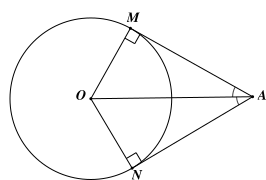
Cho đường tròn \[\left( O \right)\] và hai điểm \[M,N\] thuộc đường tròn \[\left( O \right).\] Nếu hai tiếp tuyến của đường tròn \[\left( O \right)\] tại \[M,N\] cắt nhau tại \[A\] thì điểm \[A\] cách đều hai tiếp điểm. Tức là, \[AM = AN.\]
Vậy ta chọn phương án C.
Câu 5:
Cho đường tròn \[\left( I \right)\] và hai điểm \[P,Q\] thuộc đường tròn \[\left( I \right).\] Nếu hai tiếp tuyến của đường tròn \[\left( I \right)\] tại \[P,Q\] cắt nhau tại \[E\] thì
 Xem đáp án
Xem đáp án
Đáp án đúng là: A

Cho đường tròn \[\left( I \right)\] và hai điểm \[P,Q\] thuộc đường tròn \[\left( I \right).\] Nếu hai tiếp tuyến của đường tròn \[\left( I \right)\] tại \[P,Q\] cắt nhau tại \[E\] thì \[IE\] là tia phân giác của \[\widehat {PIQ}.\]
Vậy ta chọn phương án A.
Câu 6:
II. Thông hiểu
Cho hình vẽ dưới đây biết \(AB,\,\,CB\) là hai tiếp tuyến của đường tròn \(\left( D \right).\)
![Cho hình vẽ dưới đây biết A B , C B là hai tiếp tuyến của đường tròn ( D ) .Giá trị của \[x\] bằng (ảnh 1)](https://video.vietjack.com/upload2/images/1731473440/1731474154-image5.png)
Giá trị của \[x\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Quan sát hình vẽ, ta thấy \[BA,BC\] là hai tiếp tuyến của đường tròn \[\left( D \right).\]
Áp dụng tính chất hai tiếp tuyến cắt nhau, ta được \[BA = BC.\]
Tức là, \[4x - 9 = 15\]
\[4x = 24\]
\[x = 6.\]
Vậy ta chọn phương án B.
Câu 7:
Hai tiếp tuyến tại \[B\] và \[C\] của đường tròn \[\left( {O;R} \right)\] cắt nhau tại \[A.\] Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
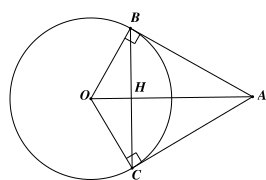
Gọi \[H\] là giao điểm của \[BC\] và \[OA.\]
Xét đường tròn \[\left( O \right)\] có hai tiếp tuyến tại \[B\] và \[C\] cắt nhau tại \[A\] nên áp dụng tính chất hai tiếp tuyến cắt nhau, ta được \[AB = AC.\] Do đó điểm \[A\] nằm trên đường trung trực của đoạn \[BC\] (1)
Đường tròn \[\left( O \right)\] có \[OB = OC = R\] nên điểm \[O\] nằm trên đường trung trực của đoạn \[BC\] (2)
Từ (1), (2), ta thu được \[OA\] là đường trung trực của đoạn \[BC.\]
Suy ra \[OA \bot BC\] tại \[H\] là trung điểm của \[BC.\]
Do đó ta chưa kết luận được \[H\] có là trung điểm của \[OA\] hay không.
Vì vậy phương án A, B, C đúng và phương án D sai.
Vậy ta chọn phương án D.
Câu 8:
Cho điểm \[M\] nằm ngoài đường tròn \[\left( I \right)\] và \[ME,MF\] là hai tiếp tuyến của đường tròn này tại \[E,F.\] Cho biết \[\widehat {EMF} = 60^\circ .\] Tam giác \[EMF\] là tam giác gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
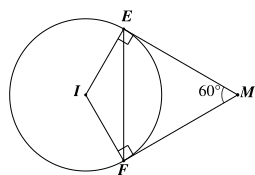
Vì \[ME,MF\] là hai tiếp tuyến của đường tròn \[\left( I \right)\] nên áp dụng tính chất hai tiếp tuyến cắt nhau, ta được \[ME = MF.\] Do đó tam giác \[EMF\] cân tại \[M.\]
Mà \[\widehat {EMF} = 60^\circ \] nên tam giác \[EMF\] đều.
Vậy ta chọn phương án C.
Câu 9:
Hai tiếp tuyến tại \[B\] và \[C\] của đường tròn \[\left( {O;R} \right)\] cắt nhau tại \[A.\] Vẽ đường kính \[CD\] đường tròn \[\left( O \right).\] Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
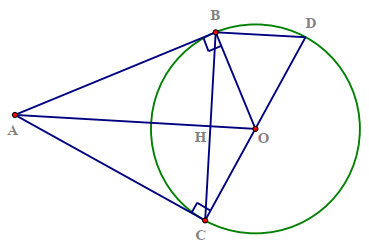
Gọi \[H\] là giao điểm của \[BC\] và \[OA.\]
Xét đường tròn \[\left( O \right)\] có hai tiếp tuyến tại \[B\] và \[C\] cắt nhau tại \[A\] nên áp dụng tính chất hai tiếp tuyến cắt nhau, ta được \[AB = AC.\] Do đó điểm \[A\] nằm trên đường trung trực của đoạn \[BC\] (1)
Đường tròn \[\left( O \right)\] có \[OB = OC = R\] nên điểm \[O\] nằm trên đường trung trực của đoạn \[BC\] (2)
Từ (1), (2), ta thu được \[OA\] là đường trung trực của đoạn \[BC.\]
Suy ra \[OA \bot BC\] tại \[H\] là trung điểm của \[BC.\] (3)
Đường tròn \[\left( O \right)\] có \[CD\] là đường kính nên tâm \[O\] là trung điểm \[CD\] hay \[OC = OD = \frac{{CD}}{2} = BO.\]
Xét tam giác \[BCD\] có \[BO\] là đường trung tuyến ứng với cạnh \[CD\] và \[BO = \frac{{CD}}{2}\] nên tam giác \[BCD\] vuông tại \[B\] hay \[BD \bot BC\] (4)
Từ (3), (4), ta suy ra \[BD\,{\rm{//}}\,OA.\]
Vậy ta chọn phương án A.
Câu 10:
Cho đường tròn \[\left( O \right)\] đường kính \[AD.\] Vẽ tiếp tuyến \[AC\] tại \[A\] của đường tròn, từ \[C\] trên tiếp tuyến đó vẽ tiếp tuyến thứ hai \[CM\] của đường tròn \[\left( O \right)\] (\[M\] là tiếp điểm và \[M\] khác \[A\]) cắt \[AD\] tại \[B.\] Giả sử \[AC = 6{\rm{\;cm}},AB = 8{\rm{\;cm}}.\] Độ dài \[BM\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
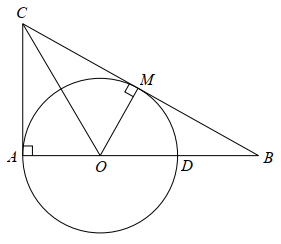
Vì \[AC\] là tiếp tuyến của đường tròn \[\left( O \right)\] nên \[AC \bot AO\] tại \[A.\]
Áp dụng định lí Pythagore cho tam giác \[ABC\] vuông tại \[A,\] ta được:
\[B{C^2} = A{B^2} + A{C^2} = {8^2} + {6^2} = 100.\] Suy ra \[BC = 10{\rm{\;(cm)}}{\rm{.}}\]
Vì \[AC,\,\,CM\] là hai tiếp tuyến của đường tròn \[\left( O \right)\] nên áp dụng tính chất hai tiếp tuyến cắt nhau, ta được \[CM = CA = 6{\rm{\;(cm)}}{\rm{.}}\]
Ta có \[BM = BC - CM = 10 - 6 = 4{\rm{\;(cm)}}{\rm{.}}\]
Vậy ta chọn phương án D.
Câu 11:
Hai tiếp tuyến tại \[A\] và \[B\] của đường tròn \[\left( O \right)\] cắt nhau tại \[I.\] Đường thẳng qua \[I\] vuông góc với \[IA\] cắt \[OB\] tại \[K.\] Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
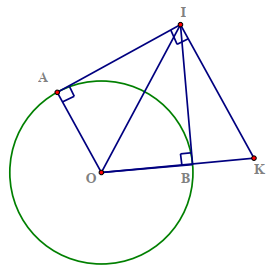
Vì đường tròn \[\left( O \right)\] có \[IA,IB\] là hai tiếp tuyến cắt nhau tại \[I\] nên \[\widehat {AOI} = \widehat {KOI}.\]
Lại có \[OA\,{\rm{//}}\,KI\] (vì cùng vuông góc với \[AI\]) nên \[\widehat {AOI} = \widehat {KIO}\] (cặp góc so le trong)
Do đó \[\widehat {KOI} = \widehat {KIO}.\]
Vì vậy tam giác \[KOI\] cân tại \[K.\]
Vậy ta chọn phương án A.
Câu 12:
Cho đường tròn \[\left( {O;R} \right)\] đường kính \[BC,\] lấy điểm \[A \in \left( O \right).\] Gọi \[H\] là trung điểm của \[AC.\] Tia \[OH\] cắt đường tròn \[\left( O \right)\] tại \[M.\] Từ \[A\] vẽ tiếp tuyến với đường tròn \[\left( O \right)\] cắt tia \[OM\] tại \[N.\] Cho các khẳng định sau:
(i) \[OH \cdot ON = {R^2}.\]
(ii) \[CN\] là tiếp tuyến của \[\left( O \right).\]
Kết luận nào sau đây là đúng nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
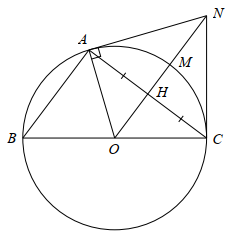
⦁ Đường tròn \[\left( O \right)\] có \[OA = OC = R\] nên tam giác \[OAC\] cân tại \[O.\]
Tam giác \[OAC\] cân tại \[O\] có \[OH\] là đường trung tuyến nên \[OH\] cũng là đường cao của tam giác, do đó \[OH \bot AC\] hay \[\widehat {OHA} = 90^\circ .\]
Vì \[AN\] là tiếp tuyến của đường tròn \[\left( O \right)\] nên \[OA \bot AN\] hay \[\widehat {OAN} = 90^\circ .\]
Xét \[\Delta OHA\] và \[\Delta OAN,\] có:
\[\widehat {OHA} = \widehat {OAN} = 90^\circ ;\] \[\widehat {AON}\] là góc chung.
Do đó (g.g). Suy ra \[\frac{{OH}}{{OA}} = \frac{{OA}}{{ON}}.\]
Vì vậy \[OH \cdot ON = O{A^2} = {R^2}.\] Do đó khẳng định (i) là đúng.
⦁ Tam giác \[OAC\] cân tại \[O\] có \[OH\] là đường trung tuyến nên \[OH\] cũng là đường phân giác của tam giác, do đó \[\widehat {AOH} = \widehat {COH}.\]
Xét \[\Delta AON\] và \[\Delta CON,\] có:
\[OA = OC = R;\] \[\widehat {AON} = \widehat {CON};\] \[ON\] là cạnh chung.
Do đó \[\Delta AON = \Delta CON\] (c.g.c).
Suy ra \[\widehat {OAN} = \widehat {OCN}.\] Nên \[\widehat {OCN} = 90^\circ .\]
Vì vậy \[OC \bot CN\] tại \[C\] hay \[CN\] là tiếp tuyến của \[\left( O \right).\] Do đó khẳng định (ii) là đúng.
Vậy ta chọn phương án C.
Câu 13:
III. Vận dụng
Cho nửa đường tròn \[\left( {O;R} \right)\] đường kính \[AB.\] Vẽ các tia tiếp tuyến \[Ax,By\] với nửa đường tròn. Lấy điểm \[M\] di động trên tia \[Ax,\] điểm \[N\] di động trên tia \[By\] sao cho \[AM \cdot BN = {R^2}.\] Cho các nhận định sau:
(i) \[MN\] là tiếp tuyến của đường tròn \[\left( O \right).\]
(ii) \[\widehat {MON} = 90^\circ .\]
Kết luận nào sau đây là đúng nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
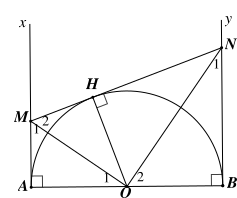
⦁ Kẻ \[OH \bot MN\] tại \[H.\]
Vì \[AM \cdot BN = {R^2} = AO \cdot BO\] nên \[\frac{{AM}}{{BO}} = \frac{{AO}}{{BN}}.\]
Xét \[\Delta AOM\] và \[\Delta BNO,\] có:
\[\widehat {OAM} = \widehat {OBN} = 90^\circ \] (vì \[AM,BN\] là các tiếp tuyến của \[\left( O \right)\]);
\[\frac{{AM}}{{BO}} = \frac{{AO}}{{BN}}\] (chứng minh trên).
Do đó (c.g.c)
Suy ra \[\widehat {{M_1}} = \widehat {{O_2}};\] \[\widehat {{O_1}} = \widehat {{N_1}}\] và \[\frac{{AM}}{{BO}} = \frac{{OM}}{{ON}}\] hay \[\frac{{AM}}{{OM}} = \frac{{BO}}{{ON}}.\]
Vì tam giác \[AOM\] vuông tại \[A\] nên \[\widehat {{M_1}} + \widehat {{O_1}} = 90^\circ .\] Suy ra \[\widehat {{O_1}} + \widehat {{O_2}} = 90^\circ .\]
Ta có \[\widehat {AOB} = 180^\circ \] hay \[\widehat {{O_1}} + \widehat {MON} + \widehat {{O_2}} = 180^\circ .\]
Tức là, \[\widehat {MON} = 180^\circ - \left( {\widehat {{O_1}} + \widehat {{O_2}}} \right) = 180^\circ - 90^\circ = 90^\circ .\] Do đó (ii) là nhận định đúng.
⦁ Xét \[\Delta AOM\] và \[\Delta ONM,\] có:
\[\widehat {OAM} = \widehat {MON} = 90^\circ ;\]
\[\frac{{AM}}{{OM}} = \frac{{AO}}{{ON}}\] (do \[\frac{{AM}}{{OM}} = \frac{{BO}}{{ON}},\,\,AO = BO).\]
Do đó (c.g.c)
Suy ra \[\widehat {{M_1}} = \widehat {{M_2}}.\]
Xét \[\Delta AOM\] và \[\Delta HOM,\] có:
\[\widehat {OAM} = \widehat {OHM} = 90^\circ ;\] \[OM\] là cạnh chung; \[\widehat {{M_1}} = \widehat {{M_2}}\]
Do đó \[\Delta AOM = \Delta HOM\] (cạnh huyền – góc nhọn)
Suy ra \[OA = OH,\] mà \(OA = R\) nên \(OH = R\).
Vì \[OH = R\] và \[OH \bot MN\] tại \[H\] nên \[MN\] là tiếp tuyến của đường tròn \(H.\)
Do đó (i) là nhận định đúng.
Vậy ta chọn phương án C.
Câu 14:
Cho đường tròn \[\left( O \right),\] từ một điểm \[M\] ở ngoài \[\left( O \right),\] vẽ hai tiếp tuyến \[MA\] và \[MB\] sao cho \[\widehat {AMB}\] bằng \[120^\circ .\] Biết chu vi tam giác \[MAB\] là \[6\left( {3 + 2\sqrt 3 } \right){\rm{\;cm}}.\] Khi đó độ dài dây \[AB\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
![Cho đường tròn \[\left( O \right),\] từ một điểm \[M\] ở ngoài \[\lCho đường tròn ( O ) , từ một điểm M ở ngoài ( O ) , vẽ hai tiếp tuyến M A và M B sao cho ˆ A M B bằng 120 ∘ . Biết chu vi tam giác M A B là 6 ( 3 + 2 √ 3 ) c m . Khi đó độ dài dây A B bằngeft( O \right),\] vẽ hai tiếp tuyến \[MA\] và \[MB\] sao cho \[\widehat {AMB}\] bằng \[120^\circ .\] Biết chu vi tam giác \[ (ảnh 1)](https://video.vietjack.com/upload2/images/1731473440/1731474154-image13.png)
Ta có \[MA,MB\] là hai tiếp tuyến của \[\left( O \right)\] cắt nhau tại \(M\) nên \[MA = MB\] và \[MO,\,\,OM\] lần lượt là tia phân giác của \[\widehat {AMB},\,\,\widehat {AOB}.\]
Khi đó \[\widehat {AMO} = \widehat {OMB} = \frac{{\widehat {AMB}}}{2} = \frac{{120^\circ }}{2} = 60^\circ .\]
Ta có \[MA\] là tiếp tuyến của \[\left( O \right)\] nên \[MA \bot OA\] tại \[A.\]
Vì tam giác \[OAM\] vuông tại \[A\] nên \[AM = AO \cdot \cot \widehat {AMO} = R \cdot \cot 60^\circ = \frac{{R\sqrt 3 }}{3}.\]
Suy ra \[MB = MA = \frac{{R\sqrt 3 }}{3}.\]
Vì tam giác \[OAM\] vuông tại \[A\] nên \[\widehat {AMO} + \widehat {AOM} = 90^\circ .\]
Suy ra \[\widehat {AOM} = 90^\circ - \widehat {AMO} = 90^\circ - 60^\circ = 30^\circ .\]
Ta có \[OM\] là tia phân giác của \[\widehat {AOB}\] nên \[\widehat {AOB} = 2\widehat {AOM} = 2 \cdot 30^\circ = 60^\circ .\]
Xét tam giác \[OAB\] có \[OA = OB = R\] và \[\widehat {AOB} = 60^\circ \] nên tam giác \[OAB\] là tam giác đều.
Khi đó \[AB = OA = OB = R.\]
Ta có chu vi tam giác \[MAB\] là \(MA + MB + AB\)
Theo bài chu vi tam giác \[MAB\] bằng \[6\left( {3 + 2\sqrt 3 } \right){\rm{\;cm,}}\] suy ra:
\[\frac{{R\sqrt 3 }}{3} + \frac{{R\sqrt 3 }}{3} + R = 6\left( {3 + 2\sqrt 3 } \right)\,\]
\[R \cdot \left( {\frac{{2\sqrt 3 + 3}}{3}} \right) = 6\left( {3 + 2\sqrt 3 } \right)\]
\[R = 18{\rm{\;(cm)}}{\rm{.}}\]
Vì vậy \[AB = R = 18{\rm{\;(cm)}}{\rm{.}}\] Vậy ta chọn phương án C.
Câu 15:
Một thủy thủ đang ở trên cột buồm của một con tàu, cách mặt nước biển \[10{\rm{\;m}}.\] Biết bán kính Trái Đất là khoảng \[6\,\,400{\rm{\;km}}.\] Tầm nhìn xa tối đa (làm tròn kết quả đến hàng phần nghìn của km) của thủy thủ đó bằng khoảng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
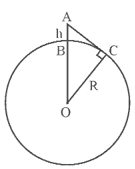
Đổi: \[10{\rm{\;m}} = 0,01{\rm{\;km}}.\]
Gọi \[O\] là tâm Trái Đất và \[R\] là bán kính Trái Đất. Suy ra \[R = 6400{\rm{\;km}}.\]
Ta có điểm \[B\] biểu diễn vị trí con tàu và điểm \[A\] biểu diễn vị trí của thủy thủ.
Suy ra \[h = AB = 10{\rm{\;(m)}}{\rm{.}}\]
Lại có điểm \[A\] biểu diễn vị trí của thủy thủ và điểm \[C\] biểu diễn điểm xa nhất mà thủy thủ nhìn thấy. Khi đó độ dài đoạn \[AC\] gọi là tầm nhìn xa tối đa từ điểm \[A.\]
Vì \[AC\] là tiếp tuyến của đường tròn \[\left( {O;R} \right)\] tại \[C\] nên \[AC \bot OC\] tại \[C.\]
Áp dụng định lí Pythagore cho tam giác \[AOC\] vuông tại \[C,\] ta được: \[O{A^2} = A{C^2} + O{C^2}.\]
Suy ra \[A{C^2} = O{A^2} - O{C^2} = {\left( {OB + AB} \right)^2} - O{C^2}\]
\[A{C^2} = {\left( {R + h} \right)^2} - {R^2} = {\left( {6\,\,400 + 0,01} \right)^2} - 6\,\,{400^2} = 128,0001.\]
Khi đó \[AC \approx 11,314{\rm{\;(km)}}{\rm{.}}\]
Do đó tầm nhìn xa tối đa của thủy thủ đó bằng khoảng \[11,314{\rm{\;km}}.\]
Vậy ta chọn phương án D.
