Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 10)
-
161 lượt thi
-
9 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Giải phương trình và hệ phương trình sau:
 Xem đáp án
Xem đáp án
Ta có: .
Do đó phương trình có hai nghiệm phân biệt
Vậy tập nghiệm phương trình S = {-3;1}.
Câu 5:
Cho hàm số y = x2 có đồ thị (P).
1) Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy.
2) Tìm giá trị nguyên của tham số m để đường thẳng cắt (P) tại hai điểm phân biệt có hoành độ lần lượt là x1 , x2 thỏa mãn x1 < 2024 < x2.
 Xem đáp án
Xem đáp án
1) Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy.
Bảng giá trị:
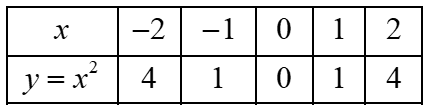
Đồ thị hàm số là một Parabol (P) đi qua các điểm
2) Tìm giá trị nguyên của tham số m để đường thẳng cắt (P) tại hai điểm phân biệt có hoành độ lần lượt là thỏa mãn .
Hoành độ giao điểm của (d) và (P) là nghiệm phương trình:
Đường thẳng (d) cắt (P) tại 2 điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt nên
(luôn đúng với mọi m).
Do đó phương trình (1) luôn có 2 nghiệm phân biệt hay đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt có hoành độ lần lượt là với mọi giá trị m.
Ta có:
(vì cần tìm m có giá trị nguyên)
Vậy thì (d) cắt (P) tại hai điểm phân biệt có hoành độ lần lượt là thỏa mãn .
Câu 6:
Một công ty dự định thuê một số xe lớn cùng loại để chở vừa hết 210 người đi du lịch Mũi Né. Nhưng thực tế, công ty lại thuê toàn bộ xe nhỏ hơn cùng loại. Biết rằng số xe nhỏ phải thuê nhiều hơn số xe lớn là 2 chiếc thì mới chở vừa hết số người trên và mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người. Tính số xe nhỏ đã thuê.
 Xem đáp án
Xem đáp án
Gọi số xe nhỏ (chiếc) công ty đã thuê là .
Do đó số xe lớn (chiếc) công ty dự định thuê là x - 2.
Số xe lớn và nhỏ đều chở vừa hết 210 người nên:
Số người trên xe nhỏ là: (người)
Số người trên xe lớn là: (người)
Theo đề mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người, nên ta có phương trình:
Vậy công ty đã thuê 7 chiếc xe nhỏ.
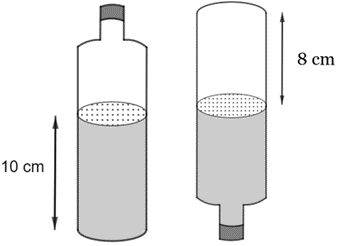
Câu 7:
 Xem đáp án
Xem đáp án
Gọi R (cm) là bán kính đáy chai (R > 0).
Thể tích nước trong chai (hình trụ có chiều cao 10 cm) là:
Thể tích không chứa nước trong chai khi lật ngược chai (hình trụ có chiều cao 8 cm) là:
Thể tích của chai là tổng thể tích của nước và phần không chứa nước trong chai khi lật ngược chai lại, nên ta có:
(do R > 0)
Vậy bán kính của đáy chai là 5 cm.
Câu 8:
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn, từ A vẽ hai tiếp tuyến AB, AC (B, C là hai tiếp điểm).
1) Chứng minh tứ giác ABOC nội tiếp.
2) Vẽ đường kính CE, nối AE cắt đường tròn (O) tại điểm thứ hai là F.
Chứng minh AB2 = AE.AF.
3) Cho OA cắt BC tại H, BF cắt OA tại I. Chứng minh I là trung điểm của AH.
 Xem đáp án
Xem đáp án
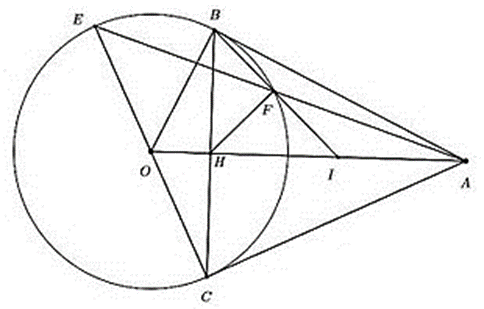
1) Xét tứ giác ABOC có:
(AC, AB lần lượt là tiếp tuyến tại B, C của (O))
Vậy tứ giác ABOC nội tiếp (hai góc đối bù nhau).
2) Xét và có:
là góc chung
(cùng bằng của (O))
Do đó
(tính chất hai tam giác đồng dạng)
.
3) Xét (O) có AB, AC lần lượt là tiếp tuyến tại B, C của (O), .
tại H
Xét ABO vuông tại B, đường cao BH, ta có:
Do đó
Xét AEO và AHF, ta có:
là góc chung
Do đó
(Hai góc tương ứng)
Mà (hai góc kề bù)
Nên hay
Suy ra tứ giác OHFE nội tiếp (Hai góc đối bù nhau)
(Tính chất tứ giác nội tiếp)
Kéo dài AO cắt (O) tại K (O nằm giữa A và K, ta có: )
(cùng bù )
Xét (O), ta có:
(Góc nội tiếp chắn nửa đường tròn)
Mặt khác, ta có tại H (cmt)
Do đó: EB // AK (cùng vuông góc với BC) (Hai góc so le trong)
Suy ra
Xét (O), ta có: (cùng bằng của (O))
Trong vuông tại B, ta có:
Ta có: tại F
Xét tam giác BHI vuông tại H, đường cao HF, ta có:
Xét IAF và IBA, ta có:
là góc chung
( cùng chắn cung BF của (O), là hai góc so le trong của EF // AK)
Vậy
Từ (1) và (2)
=> IH = IA hay i là trung điểm ah.
Câu 9:
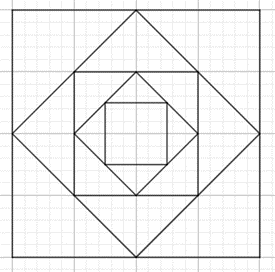
Từ hình vuông đầu tiên, bạn Hùng vẽ hình vuông thứ hai có các đỉnh là trung điểm của các cạnh hình vuông thứ nhất, vẽ tiếp hình vuông thứ ba có các đỉnh là trung điểm của các cạnh hình vuông thứ hai và cứ tiếp tục như vậy (xem hình minh họa bên). Giả sử hình vuông thứ bảy có diện tích bằng 32 cm2. Tính diện tích hình vuông thứ năm.
 Xem đáp án
Xem đáp án
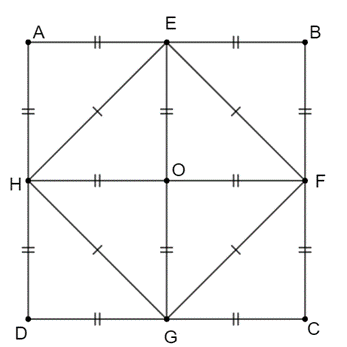
Xét hình vuông ABCD, gọi E, F, G, H lần lượt là trung điểm AB, BC, CD, DA.
Khi đó hình vuông EFGH có các đỉnh là trung điểm của các cạnh hình vuông ABCD
Dễ dàng nhận thấy
(hoặc trường hợp hai cạnh góc vuông).
Do đó
Quay lại bài toán, gọi lần lượt là điện tích của các hình vuông 1; 2; 3; 4; 5; 6; 7.
Theo nhận xét, ta có: Diện tích hình vuông bất kì bằng hai lần diện tích hình vuông có các đỉnh là trung điểm của các cạnh hình vuông đã cho.
Do đó ta có:
Vậy diện tích hình vuông thứ 5 là
