15 câu trắc nghiệm Toán 9 Chân trời sáng tạo Bài 1. Đường tròn có đáp án
-
65 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Tâm đối xứng của đường tròn là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Tâm đối xứng của đường tròn là tâm của đường tròn đó.
Vậy ta chọn phương án D.
Câu 2:
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đường tròn là hình có trục đối xứng.
Mỗi đường thẳng đi qua tâm của đường tròn là một trục đối xứng của đường tròn.
Do đó đường tròn có vô số trục đối xứng.
Vậy ta chọn phương án D.
Câu 3:
Cho đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và một điểm \[K\] bất kì. Biết rằng \[OK = 7{\rm{\;cm}}.\] Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta thấy đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] có bán kính \[R = 5{\rm{\;(cm)}}{\rm{.}}\]
Vì \[7{\rm{\;(cm)}} > 5{\rm{\;(cm)}}\] nên \[OK > R.\]
Do đó điểm \[K\] nằm ngoài đường tròn \[\left( {O;5{\rm{\;cm}}} \right).\]
Vậy ta chọn phương án B.
Câu 4:
Cho đường tròn \[\left( O \right)\] đường kính \[AB\] và dây \[CD\] không đi qua tâm. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có trong một đường tròn, đường kính là dây cung lớn nhất.
Trong đường tròn \[\left( O \right)\] có\[AB\] là đường kính và dây \[CD\] không đi qua tâm nên \[AB > CD.\]
Vậy ta chọn phương án B.
Câu 5:
Cho hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] với \[R > r\] cắt nhau tại hai điểm phân biệt và \[OO' = d.\] Chọn khẳng định đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
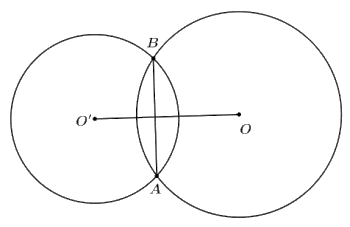
Ta thấy hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] với \[R > r\] cắt nhau khi \[R - r < d < R + r\] với \[R > r.\] </>
Do đó ta chọn phương án D.
Câu 6:
II. Thông hiểu
Cho hình chữ nhật \[ABCD\] có \[AC = 16{\rm{\;cm}}.\] Biết rằng bốn điểm \[A,B,C,D\] cùng thuộc một đường tròn. Gọi \[O\] là giao điểm của hai đường chéo \[AC\] và \[BD.\] Tâm và bán kính của đường tròn đó là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
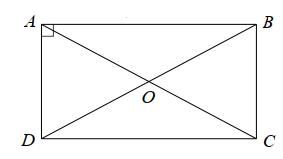
Ta có \[O\] là giao điểm của hai đường chéo \[AC\] và \[BD.\]
Suy ra \[O\] là trung điểm của \[AC\] và \[BD.\]
Do đó \[OA = OC\] và \[OB = OD.\]
Mà \[AC = BD\] (do \[AC\] và \[BD\] là hai đường chéo của hình chữ nhật \[ABCD\]).
Suy ra \[OA = OC = OB = OD.\]
Như vậy bốn điểm \[A,B,C,D\] cùng thuộc đường tròn tâm \[O\] bán kính \[OA.\]
Vì \[O\] là trung điểm của \[AC\] nên \[OA = \frac{{AC}}{2} = \frac{{16}}{2} = 8{\rm{\;(cm)}}{\rm{.}}\]
Vậy đường tròn cần tìm có tâm \[O\] bán kính \[R = OA = 8{\rm{\;(cm)}}\].
Do đó ta chọn phương án C.
Câu 7:
Cho đường tròn \[\left( O \right)\] có bán kính \[R = 5{\rm{\;cm}}.\] Khoảng cách từ tâm đến dây \[AB\] là \[3{\rm{\;cm}}.\] Độ dài dây \[AB\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C

Kẻ \[OH \bot AB\] tại \[H.\]
Vì khoảng cách từ tâm đến dây \[AB\] là \[3{\rm{\;cm}}\] nên ta có \[OH = 3{\rm{\;cm}}.\]
Áp dụng định lí Pythagore cho tam giác \[OHB\] vuông tại \[H,\] ta được: \[O{H^2} + H{B^2} = O{B^2}.\]
Suy ra \[H{B^2} = O{B^2} - O{H^2} = {R^2} - O{H^2} = {5^2} - {3^2} = 16\]. Do đó \[HB = 4{\rm{\;(cm)}}{\rm{.}}\]
Tam giác \[OAB\] cân tại \[O\] (do \[OA = OB = R\]) có \[OH\] là đường cao nên \[OH\] cũng là đường trung tuyến của tam giác. Do đó \[H\] là trung điểm \[AB.\]
Suy ra \[AB = 2 \cdot HB = 2 \cdot 4 = 8{\rm{\;(cm)}}{\rm{.}}\]
Vậy ta chọn phương án B.
Câu 8:
Cho hai đường tròn \(\left( O \right)\) đường kính \(7{\rm{\;cm}}\) và \(\left( {I;\,4{\rm{\;cm}}} \right).\) Biết \(OI = 1{\rm{\;cm,}}\) vị trí tương đối của hai đường tròn \(\left( O \right)\) và \(\left( I \right)\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Bán kính của đường tròn \(\left( O \right)\) là: \(7:2 = 3,5{\rm{\;(cm)}}{\rm{.}}\)
Ta có \(OI = 1{\rm{\;cm}} < 4{\rm{\;cm}} - 3,5{\rm{\;cm}}\)
Do đó đường tròn \(\left( I \right)\) đựng đường tròn \(\left( O \right).\)
Câu 9:
Cho hai đường tròn \(\left( {O;1{\rm{\;cm}}} \right)\) và \(\left( {I;3{\rm{\;cm}}} \right)\) cắt nhau, đoạn thẳng \(OI\) có độ dài là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì hai đường tròn \(\left( {O;1{\rm{\;cm}}} \right)\) và \(\left( {I;3{\rm{\;cm}}} \right)\) cắt nhau nên ta có:
\[3{\rm{\;cm}} - 1{\rm{\;cm}} < OI < 3{\rm{\;cm}} + 1{\rm{\;cm}}\]
Hay \[2{\rm{\;cm}} < OI < 4{\rm{\;cm}}.\]
Trong các phương án đã cho, ta thấy chỉ có giá trị \(OI = 3{\rm{\;cm}}\) thỏa mãn điều kiện trên.
Vậy ta chọn phương án B.
Câu 10:
Cho hai đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và \(\left( {I;R} \right)\) với \(R < 5{\rm{\;cm}}.\) Biết \(OI = 3{\rm{\;cm}},\) giá trị của \(R\) để hai đường tròn tiếp xúc trong là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Để hai đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và \(\left( {I;R} \right)\) tiếp xúc trong thì \(OI = 5 - R > 0\)
Suy ra \[R = 5 - OI = 5 - 3 = 2{\rm{\;(cm)}}{\rm{.}}\]
Câu 11:
Cho hai đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và \(\left( {I;R} \right)\). Biết \(OI = 7{\rm{\;cm}},\) giá trị của \(R\) để hai đường tròn ở ngoài nhau là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Để hai đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và \(\left( {I;R} \right)\) ở ngoài nhau thì \(OI > 5 + R\)
Hay \(7 > 5 + R\) suy ra \(R < 2{\rm{\;cm}}.\)
Trong các phương án trên, ta thấy chỉ có giá trị \(R = 1{\rm{\;cm}}\) thỏa mãn điều kiện trên.
Vậy ta chọn phương án A.
Câu 12:
Cho đường tròn \(\left( {I;R} \right)\) có đường kính \[12{\rm{\;dm}}\] và đường tròn \(\left( {J;R'} \right)\) có đường kính \[18{\rm{\;dm}}.\] Nếu \(IJ = 15{\rm{\;dm}}\) thì hai đường tròn \[\left( I \right),\,\,\left( J \right)\] có vị trí tương đối là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
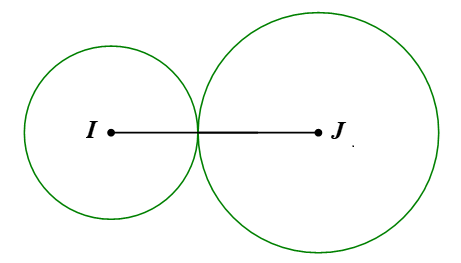
Đường tròn \(\left( I \right)\) có bán kính \[R = \frac{{12}}{2} = 6{\rm{\;(dm)}}{\rm{.}}\]
Đường tròn \(\left( J \right)\) có bán kính \[R' = \frac{{18}}{2} = 9{\rm{\;(dm)}}{\rm{.}}\]
Ta có \[R + R' = 6 + 9 = 15{\rm{\;(dm)}}{\rm{.}}\]
Do đó \[R + R' = IJ.\]
Vậy hai đường tròn \[\left( I \right),\,\,\left( J \right)\] tiếp xúc ngoài với nhau.
Do đó ta chọn phương án B.
Câu 13:
III. Vận dụng
Cho đường tròn \[\left( {O;R} \right)\] có hai dây \[AB,CD\] vuông góc với nhau tại \[M.\] Giả sử \[AB = 16{\rm{\;cm}},CD = 12{\rm{\;cm}},MC = 2{\rm{\;cm}}.\] Kẻ \[OH \bot AB\] tại \[H,\] \[OK \bot CD\] tại \[K.\] Khi đó diện tích tứ giác \[OHMK\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
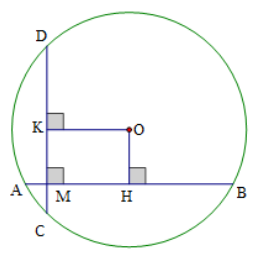
Tam giác \[OAB\] cân tại \[O\] (do \[OA = OB = R)\] có \[OH\] là đường cao nên \[OH\] cũng là đường trung tuyến của tam giác. Do đó \[H\] là trung điểm \[AB.\]
Vì vậy \[HA = HB = \frac{{AB}}{2} = \frac{{16}}{2} = 8{\rm{\;(cm)}}{\rm{.}}\]
Chứng minh tương tự, ta được \[KC = KD = \frac{{CD}}{2} = \frac{{12}}{2} = 6{\rm{\;(cm)}}{\rm{.}}\]
Ta có \[KC = KM + MC.\] Suy ra \[KM = KC - MC = 6 - 2 = 4{\rm{\;(cm)}}{\rm{.}}\]
Tứ giác \[OHMK\] có: \[\widehat {OKM} = \widehat {KMH} = \widehat {OHM} = 90^\circ \] nên tứ giác \[OHMK\] là hình chữ nhật.
Do đó \[OH = KM = 4{\rm{\;(cm)}}{\rm{.}}\]
Áp dụng định lí Pythagore cho tam giác \[OHB\] vuông tại \[H,\] ta được:
\[O{B^2} = O{H^2} + H{B^2} = {4^2} + {8^2} = 80\]. Suy ra \[R = OB = 4\sqrt 5 {\rm{\;(cm)}}{\rm{.}}\]
Áp dụng định lí Pythagore cho tam giác \[OKD\] vuông tại \[K,\] ta được: \[O{D^2} = O{K^2} + K{D^2}.\]
Suy ra \[O{K^2} = O{D^2} - K{D^2} = {R^2} - K{D^2} = {\left( {4\sqrt 5 } \right)^2} - {6^2} = 44\]
Do đó \[OK = 2\sqrt {11} {\rm{\;(cm)}}{\rm{.}}\]
Vậy diện tích hình chữ nhật \[OHMK\] là: \[S = KM \cdot OK = 4 \cdot 2\sqrt {11} = 8\sqrt {11} {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Do đó ta chọn phương án C.
Câu 14:
Trong một trò chơi, hai bạn Thủy và Tiến cùng chạy trên một đường tròn tâm \[O\] có bán kính \[20{\rm{\;m}}\] (hình vẽ).
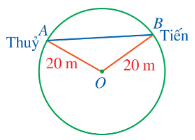
Độ dài dây \[AB\] nối vị trí của hai bạn đó không thể bằng bao nhiêu mét?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đường tròn tâm \[O\] có đường kính bằng \[2 \cdot 20 = 40{\rm{\;(m)}}.\]
Vì độ dài dây \[AB\] không thể vượt quá độ dài đường kính của đường tròn tâm \[O\] nên \[AB \le 40{\rm{\;(m)}}.\]
Tức là, không có thời điểm nào dây \[AB\] nối vị trí của hai bạn đó có độ dài lớn hơn \[40{\rm{\;m}}.\]
Vì \[41{\rm{\;(m)}} > 40{\rm{\;(m)}}\] nên độ dài dây \[AB\] nối vị trí của hai bạn đó không thể bằng \[41{\rm{\;m}}.\]
Vậy ta chọn phương án D.
Câu 15:
Cho hai đường tròn \[\left( {O;4{\rm{\;cm}}} \right)\] và \[\left( {O';3{\rm{\;cm}}} \right)\] biết \[OO' = 5{\rm{\;cm}}.\] Hai đường tròn trên cắt nhau tại \[A\] và \[B.\] Độ dài \[AB\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C

Gọi \[H\] là giao điểm của \[OO'\] và \[AB.\]
Vì \[{4^2} + {3^2} = {5^2}\] hay \(O{A^2} + O'{A^2} = O{O'^2}\) nên theo định lí Pythagore đảo, ta được tam giác \[OO'A\] vuông tại \[A.\]
Vì \[OA = OB = 4{\rm{\;(cm)}}\] nên \[O\] nằm trên đường trung trực của đoạn \[AB.\]
Chứng minh tương tự, ta được \[O'\] nằm trên đường trung trực của đoạn \[AB.\]
Khi đó \[OO'\] là đường trung trực của đoạn \[AB.\]
Vì vậy \[OO' \bot AB\] tại \[H\] và \[H\] là trung điểm \[AB.\]
Xét \[\Delta OAH\] và \[\Delta OO'A,\] có: \[\widehat {OHA} = \widehat {OAO'} = 90^\circ \] và \[\widehat {AOH}\] là góc chung.
Do đó (g.g)
Suy ra \[\frac{{AH}}{{O'A}} = \frac{{OA}}{{OO'}}\] nên \[AH = \frac{{OA}}{{OO'}} \cdot O'A = \frac{4}{5} \cdot 3 = \frac{{12}}{5}{\rm{\;(cm)}}{\rm{.}}\]
Vì \[H\] là trung điểm  nên \[AB = 2AH = 2 \cdot \frac{{12}}{5} = \frac{{24}}{5} = 4,8{\rm{\;(cm)}}{\rm{.}}\]
nên \[AB = 2AH = 2 \cdot \frac{{12}}{5} = \frac{{24}}{5} = 4,8{\rm{\;(cm)}}{\rm{.}}\]
Vậy ta chọn phương án C.
