15 câu trắc nghiệm Toán 9 Cánh diều Bài tập cuối chương VI có đáp án
-
43 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Tần số của một giá trị cho biết
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tần số của một giá trị cho biết giá trị đó xuất hiện trong mẫu dữ liệu nhiều hay ít, từ đó ta dễ dàng xác định được giá trị xuất hiện nhiều nhất, ít nhất.
Do đó ta chọn phương án B.
Câu 2:
Tần số tương đối \[{f_2}\] của giá trị \[{x_2}\] là tỉ số giữa
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tần số tương đối \[{f_2}\] của giá trị \[{x_2}\] là tỉ số giữa tần số \[{m_2}\] của \[{x_2}\] với \[n.\]
Do đó ta chọn phương án C.
Câu 3:
Nếu chiều cao mỗi cột biểu diễn tần số của nhóm số liệu thì ta có biểu đồ tần số tương đối ghép nhóm ở dạng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Nếu chiều cao mỗi cột biểu diễn tần số của nhóm số liệu thì ta có biểu đồ tần số tương đối ghép nhóm ở dạng cột.
Do đó ta chọn phương án A.
Câu 4:
Một hộp chứa 4 quả cầu trắng và 6 quả cầu xanh có kích thước và khối lượng như nhau. Lấy ngẫu nhiên 3 quả cầu từ trong hộp. Hoạt động nào sau đây không phải là biến cố của phép thử trên?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Các quả cầu trong hộp chỉ có hai màu trắng và xanh nên không thể xảy ra trường hợp lấy được ba quả cầu có ba màu.
Câu 5:
Chọn ngẫu nhiên một số tự nhiên có 3 chữ số. Số kết quả thuận lợi cho biến cố “Số được chọn chia hết cho 10” là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Các kết quả thuận lợi cho biến cố là \[100\,;\,\,110\,;\,\,120\,;\,\, \ldots \,;\,\,980\,;\,\,990.\]
Số kết quả thuận lợi cho biến cố là \(\frac{{990 - 100}}{{10}} + 1 = 90\) (kết quả).
Câu 6:
II. Thông hiểu
Một giáo viên thể dục đo chiều cao (tính theo cm) của một nhóm học sinh nữ lớp 9 được cho bởi bảng tần số sau:
|
Chiều cao của một học sinh |
149 |
150 |
153 |
155 |
158 |
160 |
163 |
|
Tần số |
2 |
1 |
4 |
6 |
7 |
8 |
5 |
Tần số của giá trị 153 và 158 lần lượt là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Quan sát bảng tần số, ta thấy:
⦁ Tần số của giá trị 153 là 4;
⦁ Tần số của giá trị 158 là 7.
Do đó tần số của giá trị 153 và 158 lần lượt là 4 và 7.
Vậy ta chọn phương án B.
Câu 7:
Biểu đồ đoạn thẳng dưới đây biểu diễn số lượng vé bán được với các mức giá khác nhau của một buổi hòa nhạc:
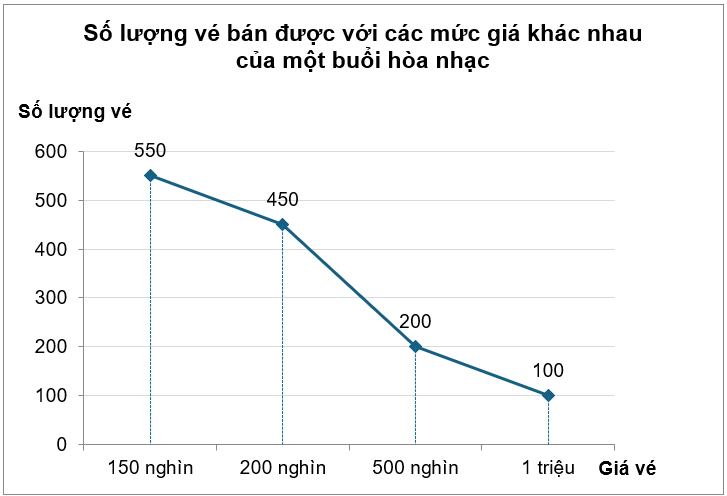
Các vé bán được của buổi hòa nhạc nhận các mức giá 150 nghìn, 200 nghìn, 500 nghìn, 1 triệu thì tần số tương ứng của các mức giá đó là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Quan sát biểu đồ, ta thấy:
⦁ Có 550 vé bán được của buổi hòa nhạc nhận các mức giá 150 nghìn.
⦁ Có 450 vé bán được của buổi hòa nhạc nhận các mức giá 200 nghìn.
⦁ Có 200 vé bán được của buổi hòa nhạc nhận các mức giá 500 nghìn.
⦁ Có 100 vé bán được của buổi hòa nhạc nhận các mức giá 1 triệu.
Do đó các vé bán được của buổi hòa nhạc nhận các mức giá 150 nghìn, 200 nghìn, 500 nghìn, 1 triệu thì tần số tương ứng của các mức giá đó là 550 vé; 450 vé; 200 vé; 100 vé.
Vậy ta chọn phương án A.
Câu 8:
Bạn Thủy thống kê số sách mà mỗi bạn trong lớp đã đọc sau tuần lễ đọc sách và ghi lại trong bảng dưới đây
Số sách (quyển) | 0 | 1 | 2 | 3 | 4 | 5 |
Số học sinh | 1 | 4 | 8 | 15 | 7 |
Biết tần số tương đối của giá trị số sách 2 quyển là \[20\% .\] Hỏi số học sinh đọc 5 quyển là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tần số của giá trị số sách 2 quyển là \[m = 8.\]
Vì tần số tương đối của giá trị số sách 2 quyển là \[20\% \] nên số học sinh của lớp là:
\[n = 8:20\% = 40.\]
Do đó số học sinh đọc 5 quyển là: \[40 - 1 - 4 - 8 - 15 - 7 = 5\] (học sinh).
Vậy ta chọn phương án C.
Câu 9:
Kết quả tham gia chạy Việt dã trong ngày Hội khỏe Phù Đổng cấp trường của khối 9 cho bởi biểu đồ sau:
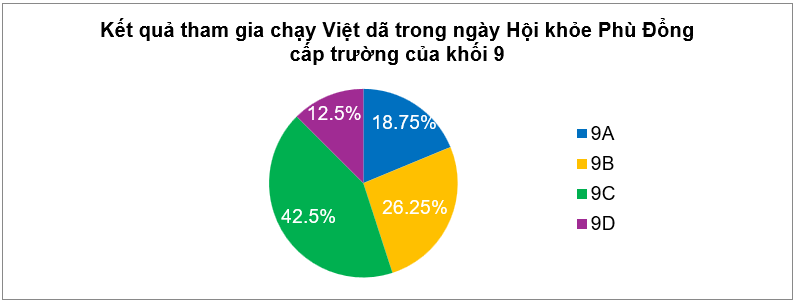
Tần số tương đối của số học sinh tham gia chạy Việt dã của lớp 9D là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Quan sát biểu đồ, ta thấy tần số tương đối của số học sinh tham gia chạy Việt dã của lớp 9D là \[12,5\% .\]
Do đó ta chọn phương án C.
Câu 10:
Một doanh nghiệp sản xuất xe ô tô khảo sát lượng xăng tiêu thụ trên 100 km của một số loại xe ô tô trên thị trường. Kết quả khảo sát 100 chiếc xe được biểu diễn như biểu đồ sau
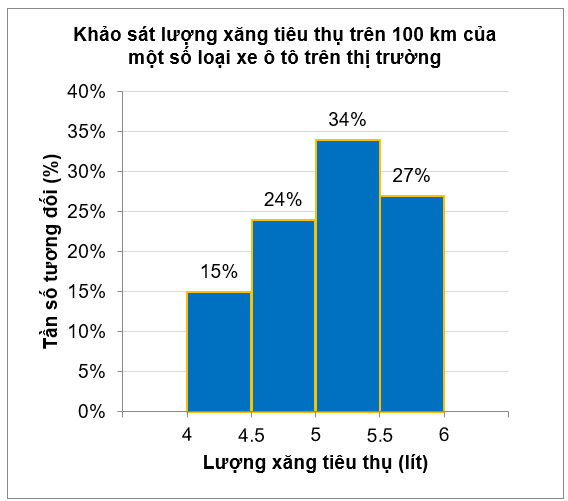
Tần số tương đối của số lượng xe ô tô tiêu thụ dưới 5 lít xăng cho 100 km là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Quan sát biểu đồ, ta thấy:
⦁ Tần số tương đối của số lượng xe ô tô tiêu thụ từ 4 đến dưới 4,5 lít xăng là \[15\% .\]
⦁ Tần số tương đối của số lượng xe ô tô tiêu thụ từ 4,5 đến dưới 5 lít xăng là \[24\% .\]
Do đó tần số tương đối của số lượng xe ô tô tiêu thụ dưới 5 lít xăng cho 100 km là:
\[15\% + 24\% = 39\% .\]
Vậy ta chọn phương án C.
Câu 11:
Lấy ngẫu nhiên hai viên bi từ một thùng có 4 bi xanh, 5 bi đỏ và 6 bi vàng. Số phần tử của không gian mẫu là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tổng số bi trong thùng là \(4 + 5 + 6 = 15\) (viên bi).
Số cách chọn ngẫu nhiên 1 viên bi là 15 cách chọn.
Số cách chọn ngẫu nhiên viên bi còn lại là 14 cách chọn.
Suy ra số cách lấy ngẫu nhiên hai viên bi từ thùng là \(15 \cdot 14 = 210\) (cách).
Tuy nhiên mỗi cách chọn đã bị tính 2 lần.
Do đó số phần tử của không gian mẫu là: \(\frac{{210}}{2} = 105\) (phần tử).
Câu 12:
Một lô hàng có 1000 sản phẩm, trong đó có 50 sản phẩm không đạt yêu cầu. Lấy ngẫu nhiên từ lô hàng đó 1 sản phẩm. Xác suất để sản phẩm lấy ra là sản phẩm tốt là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Số kết quả có thể xảy ra khi lấy 1 sản phẩm bất kỳ là 1000 kết quả.
Số sản phẩm tốt là \(1000 - 50 = 950\) (sản phẩm).
Suy ra có 950 kết quả thuận lợi cho biến cố.
Vậy xác suất xảy ra biến cố là \(P = \frac{{950}}{{1\,\,000}} = 0,95\).
Câu 13:
III. Vận dụng
Một nhà máy kiểm tra cân nặng 100 sản phẩm của một dây chuyền đóng gói bánh đang trong thời gian thử nghiệm. Cân nặng của mỗi gói bánh có tiêu chuẩn là 500 gam. Những gói bánh có khối lượng chênh lệch không quá 10 gam so với tiêu chuẩn được xem là đạt yêu cầu. Kết quả kiểm tra được biểu diễn ở biểu đồ dưới đây:
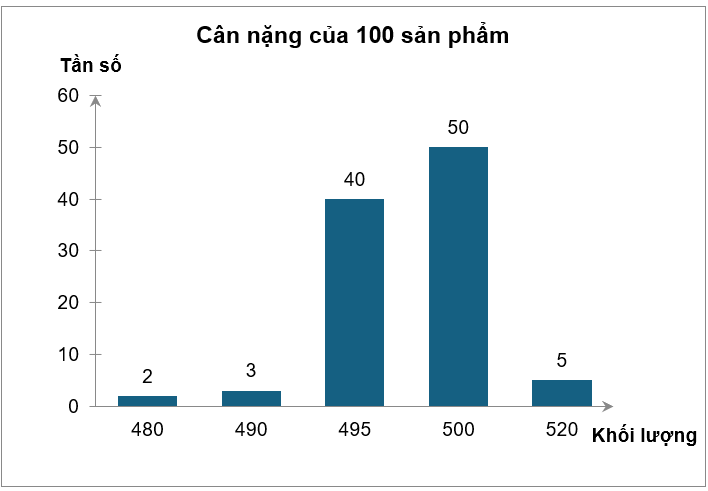
Trong 100 sản phẩm được kiểm tra, số gói bánh đạt yêu cầu chênh lệch bao nhiêu với số gói bánh không đạt yêu cầu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Quan sát biểu đồ, ta thấy:
⦁ Có 2 gói bánh có khối lượng 480 gam.
⦁ Có 3 gói bánh có khối lượng 490 gam.
⦁ Có 40 gói bánh có khối lượng 495 gam.
⦁ Có 50 gói bánh có khối lượng 500 gam.
⦁ Có 5 gói bánh có khối lượng 520 gam.
Ta có:
⦁ Cân nặng của mỗi gói bánh có tiêu chuẩn là 500 gam.
⦁ Những gói bánh có khối lượng chênh lệch không quá 10 gam so với tiêu chuẩn được xem là đạt yêu cầu.
Suy ra các gói bánh đạt yêu cầu là các gói bánh có khối lượng 490 gam; 495 gam; 500 gam.
Do đó có tổng cộng \[3 + 40 + 50 = 93\] gói bánh có khối lượng đạt yêu cầu.
Vì vậy có tổng cộng \[100 - 93 = 7\] gói bánh có khối lượng không đạt yêu cầu.
Vậy số gói bánh đạt yêu cầu chênh lệch \[93 - 7 = 86\] gói bánh so với số gói bánh không đạt yêu cầu, ta chọn phương án C.
Câu 14:
Một câu lạc bộ thể hình thống kê số lượng người đến tập mỗi ngày trong 2 tuần liên tiếp. Các số liệu được chia thành 5 nhóm sau: \[\left[ {0;10} \right),\,\,\left[ {10;20} \right),\,\,\left[ {20;30} \right),\,\,\left[ {30;40} \right),\,\,\left[ {40;50} \right).\] Sau khi ghép nhóm mẫu số liệu thu được, người ta nhận được biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng như sau:
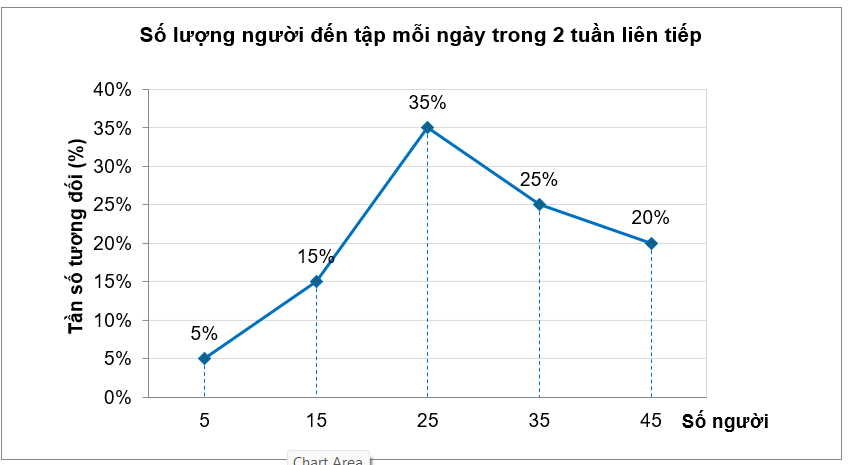
Nhóm có nhiều người đến tập nhất cao hơn nhóm có ít người đến tập nhất bao nhiêu phần trăm?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Quan sát biểu đồ, ta thấy:
⦁ Nhóm có nhiều người đến tập nhất có giá trị đại diện là \[{x_3} = 25\] (chiếm tỉ lệ \[35\% \]).
⦁ Nhóm có ít người đến tập nhất có giá trị đại diện là \[{x_1} = 5\] (chiếm tỉ lệ \[5\% \]).
Vậy nhóm có nhiều người đến tập nhất cao hơn nhóm có ít người đến tập nhất là \[35\% - 5\% = 30\% .\]
Do đó ta chọn phương án B.
Câu 15:
Đội văn nghệ của lớp 9A có 3 bạn nam và 3 bạn nữ. Cô giáo phụ trách đội chọn ngẫu nhiên hai bạn để hát song ca. Xét biến cố: “Trong hai bạn được chọn ra, có một bạn nam và một bạn nữ”. Xác suất xảy ra biến cố trên là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đánh số các bạn nam lần lượt là \[1\,;\,\,3\,;\,\,5.\]
Đánh số các bạn nữ lần lượt là \[2\,;\,\,4\,;\,\,6.\]
Để biến cố xảy ra thì trong hai bạn được chọn phải có 1 số lẻ và một số chẵn.
Bạn số 1 Bạn số 2 | 1 | 2 | 3 | 4 | 5 | 6 |
1 | \[\left( {1\,;\,\,1} \right)\] | \[\left( {2\,;\,\,1} \right)\] | \[\left( {3\,;\,\,1} \right)\] | \[\left( {4\,;\,\,1} \right)\] | \[\left( {5\,;\,\,1} \right)\] | \[\left( {6\,;\,\,1} \right)\] |
2 | \[\left( {1\,;\,\,2} \right)\] | \[\left( {2\,;\,\,2} \right)\] | \[\left( {3\,;\,\,2} \right)\] | \[\left( {4\,;\,\,2} \right)\] | \[\left( {5\,;\,\,2} \right)\] | \[\left( {6\,;\,\,2} \right)\] |
3 | \[\left( {1\,;\,\,3} \right)\] | \[\left( {2\,;\,\,3} \right)\] | \[\left( {3\,;\,\,3} \right)\] | \[\left( {4\,;\,\,3} \right)\] | \[\left( {5\,;\,\,3} \right)\] | \[\left( {6\,;\,\,3} \right)\] |
4 | \[\left( {1\,;\,\,4} \right)\] | \[\left( {2\,;\,\,4} \right)\] | \[\left( {3\,;\,\,4} \right)\] | \[\left( {4\,;\,\,4} \right)\] | \[\left( {5;{\rm{ }}4} \right)\] | \[\left( {6\,;\,\,4} \right)\] |
5 | \[\left( {1\,;\,\,5} \right)\] | \[\left( {2\,;\,\,5} \right)\] | \[\left( {3\,;\,\,5} \right)\] | \[\left( {4\,;\,\,5} \right)\] | \[\left( {5\,;\,\,5} \right)\] | \[\left( {6\,;\,\,5} \right)\] |
6 | \[\left( {1\,;\,\,6} \right)\] | \[\left( {2\,;\,\,6} \right)\] | \[\left( {3\,;\,\,6} \right)\] | \[\left( {4\,;\,\,6} \right)\] | \[\left( {5;{\rm{ }}6} \right)\] | \[\left( {6\,;\,\,6} \right)\] |
Vì một bạn không thể được chọn 2 lần nên các ô bị gạch trong bảng không có khả năng xảy ra.
Không gian mẫu của phép thử là \(\Omega = \left\{ {\left( {2;\,\,1} \right);\,\,\left( {3;\,\,1} \right);\left( {4;\,\,1} \right);...;\left( {5;\,\,6} \right)} \right\}\).
Không gian mẫu của phép thử có 30 phần tử.
Vì khả năng được chọn của các bạn là như nhau nên các kết quả của phép thử là đồng khả năng.
Có 18 kết quả thuận lợi cho biến cố là \[\left( {2\,;\,\,1} \right)\,;\,\,\left( {4\,;\,\,1} \right)\,;\,\,\left( {6\,;\,\,1} \right)\,;\,\,\left( {1\,;\,\,2} \right)\,;\,\,\left( {3\,;\,\,2} \right)\,;\,\,\left( {5\,;\,\,2} \right)\,;\,\,\left( {2\,;\,\,3} \right)\,;\,\,\left( {4\,;\,\,3} \right)\,;\]\[\left( {6\,;\,\,3} \right)\,;\,\,\left( {1\,;\,\,4} \right)\,;\,\,\left( {3\,;\,\,4} \right)\,;\,\,\left( {5\,;\,\,4} \right)\,;\,\,\left( {2\,;\,\,5} \right)\,;\,\,\left( {4\,;\,\,5} \right)\,;\,\,\left( {6\,;\,\,5} \right)\,;\,\,\left( {1\,;\,\,6} \right)\,;\,\,\left( {3\,;\,\,6} \right)\,;\,\,\left( {5\,;\,\,6} \right).\]
Vậy xác suất của biến cố là \(P = \frac{{18}}{{30}} = \frac{3}{5}\).
