15 câu trắc nghiệm Toán 9 Cánh diều Bài tập cuối chương X có đáp án
-
48 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Gọi \[l,h,R\] lần lượt là độ dài đường sinh, chiều cao và bán kính của hình trụ. Đẳng thức luôn đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Trong hình trụ, ta có độ dài đường sinh luôn bằng chiều cao của hình trụ.
Tức là, \[l = h.\]
Vậy ta chọn phương án B.
Câu 2:
Cho hình trụ nằm bên trong hình lập phương có cạnh bằng \[40{\rm{\;cm}}\] (như hình vẽ).
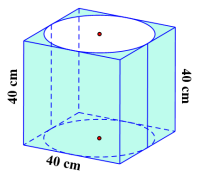
Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
⦁ Độ dài đường sinh luôn bằng chiều cao của hình trụ và bằng cạnh của hình lập phương.
Tức là, \[l = h = 40{\rm{\;cm}}.\] Do đó phương án B, D đúng.
⦁ Đường kính đáy của hình trụ bằng cạnh của hình lập phương.
Tức là, \[2r = 40{\rm{\;cm}}.\] Do đó phương án A sai, phương án C đúng.
Vậy ta chọn phương án A.
Câu 3:
Khi quay một tam giác vuông quanh đường thẳng cố định chứa một cạnh góc vuông của tam giác vuông đó thì ta được
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Khi quay một tam giác vuông quanh đường thẳng cố định chứa một cạnh góc vuông của tam giác vuông đó thì ta được một hình nón.
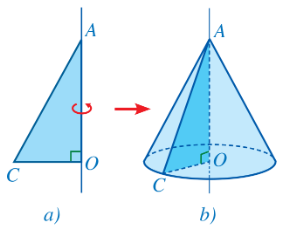
Do đó ta chọn phương án D.
Câu 4:
Cho hình nón có bán kính đáy \[r = \sqrt 3 {\rm{\;cm}},\] độ dài đường sinh \[l = 4{\rm{\;cm}}.\] Diện tích xung quanh của hình nón đó bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Diện tích xung quanh của hình nón đó là: \[{S_{xq}} = \pi rl = \pi \cdot \sqrt 3 \cdot 4 = 4\pi \sqrt 3 {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Vậy ta chọn phương án A.
Câu 5:
Nếu cắt một hình cầu bởi một mặt phẳng không đi qua tâm hình cầu thì phần chung giữa chúng là một
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Nếu cắt một hình cầu bởi một mặt phẳng không đi qua tâm hình cầu thì phần chung giữa chúng là một hình tròn.
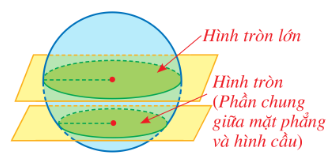
Do đó ta chọn phương án D.
Câu 6:
II. Thông hiểu
Cho hình trụ có đường kính đáy \[10{\rm{\;cm}},\] chiều cao \[4{\rm{\;cm}}.\] Diện tích xung quanh của hình trụ này là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Bán kính đáy của hình trụ đó là: \[r = \frac{{10}}{2} = 5{\rm{\;(cm)}}{\rm{.}}\]
Diện tích xung quanh của hình trụ đó là: \[{S_{xq}} = 2\pi rh = 2\pi \cdot 5 \cdot 4 = 40\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Vậy ta chọn phương án D.
Câu 7:
Một hình trụ có chiều cao bằng \(a\) và chu vi đường tròn đáy bằng \[4\pi a.\] Thể tích của khối trụ này bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Bán kính đáy của hình trụ đó là: \[r = \frac{C}{{2\pi }} = \frac{{4\pi a}}{{2\pi }} = 2a.\]
Thể tích của khối trụ đó là: \[V = \pi {r^2}h = \pi \cdot {\left( {2a} \right)^2} \cdot a = 4\pi {a^3}.\]
Vậy ta chọn phương án C.
Câu 8:
Cho hình nón có chiều cao bằng \[a\] và đường kính đường tròn đáy bằng \[2a.\] Thể tích của hình nón bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Bán kính đường tròn đáy là: \[r = \frac{{2a}}{2} = a.\]
Thể tích của hình nón là: \[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi \cdot {a^2} \cdot a = \frac{{\pi {a^3}}}{3}.\]
Vậy ta chọn phương án A.
Câu 9:
Một hình nón có độ dài đường sinh là \[9{\rm{\;dm}}\] và diện tích xung quanh bằng \[54\pi {\rm{\;d}}{{\rm{m}}^2}.\] Bán kính đáy của hình nón đó bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi \(r{\rm{\;(dm)}}\) là bán kính đáy của hình nón.
Công thức tính diện tích xung quanh của hình nón là: \[{S_{xq}} = \pi rl{\rm{\;(d}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Theo bài, ta có: \[\pi rl = 54\pi \]
Suy ra \[\pi r \cdot 9 = 54\pi \]
Do đó \[r = \frac{{54\pi }}{{9\pi }} = 6{\rm{\;(dm)}}{\rm{.}}\]
Vậy ta chọn phương án C.
Câu 10:
Một hình nón có bán kính đáy là \[13{\rm{\;cm}}\] và thể tích là \[676\pi {\rm{\;c}}{{\rm{m}}^3}.\] Độ dài đường sinh của hình nón đó làm tròn đến hàng phần trăm là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Gọi \(h{\rm{\;(cm),}}\,\,l{\rm{\;(cm)}}\) lần lượt là chiều cao và đường sinh của hình nón.
Công thức tính thể tích của hình nón là: \(V = \frac{1}{3}\pi {r^2}h{\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Theo bài, ta có: \[\frac{1}{3}\pi {r^2}h = 676\pi \]
Suy ra \[\frac{1}{3}\pi \cdot {13^2} \cdot h = 676\pi \]
Do đó \[h = \frac{{3 \cdot 676\pi }}{{\pi \cdot {{13}^2}}} = 12{\rm{\;(cm)}}{\rm{.}}\]
Ta có: \[{l^2} = {h^2} + {r^2} = {12^2} + {13^2} = 313.\]
Suy ra \[l = \sqrt {313} {\rm{\;(cm)}} \approx 17,69{\rm{\;(cm)}}{\rm{.}}\]
Vậy ta chọn phương án D.
Câu 11:
Một hình cầu có độ dài đường tròn lớn là \[30\pi {\rm{\;dm}}.\] Diện tích mặt cầu đó bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Công thức tính độ dài đường tròn lớn là: \(C = 2\pi R{\rm{\;(d}}{{\rm{m}}^2}{\rm{),}}\) trong đó \(R\) là bán kính của hình cầu.
Theo bài, ta có: \[2\pi R = 30\pi \]
Suy ra \[R = \frac{{30\pi }}{{2\pi }} = 15{\rm{\;(dm)}}{\rm{.}}\]
Diện tích của mặt cầu đã cho là:
\[S = 4\pi {R^2} = 4\pi \cdot {15^2} = 900\pi {\rm{\;(d}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Vậy ta chọn phương án C.
Câu 12:
Một hình cầu có diện tích bề mặt là \[576\pi {\rm{\;c}}{{\rm{m}}^2}.\] Thể tích của hình cầu đó bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi \(R{\rm{\;(cm)}}\) là bán kính của hình cầu.
Công thức tính diện tích bề mặt của hình cầu là: \[S = 4\pi {R^2}{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Theo bài, ta có: \[4\pi {R^2} = 576\pi .\]
Suy ra \[{R^2} = \frac{{576\pi }}{{4\pi }} = 144.\]
Do đó \[R = 12{\rm{\;(cm)}}\] (do \(R > 0).\)
Thể tích của hình cầu đó là: \[V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \cdot {12^3} = 2\,\,304\pi {\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Vậy ta chọn phương án B.
Câu 13:
III. Vận dụng
Một bồn chứa xăng hình trụ có đường kính đáy \[2,2{\rm{\;m}}\] và chiều cao \[3,5{\rm{\;m}}.\] Biết rằng, cứ \[1\,\,kg\] sơn thì sơn được \[8{\rm{\;}}{{\rm{m}}^2}.\] Giả sử bề dày thành bồn chứa xăng không đáng kể và lấy \[\pi \approx 3,14.\] Hỏi để sơn bề mặt ngoài của bồn chứa xăng hết bao nhiêu ki-lô-gam sơn (kết quả làm tròn đến hàng đơn vị)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Bán kính đáy của bồn chứa xăng là: \[r = \frac{{2,2}}{2} = 1,1{\rm{\;(m)}}{\rm{.}}\]
Diện tích toàn phần của bồn chứa xăng là:
\[{S_{tp}} = 2\pi r\left( {h + r} \right) = 2\pi \cdot 1,1 \cdot \left( {3,5 + 1,1} \right) = 10,12\pi {\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Số ki-lô-gam sơn cần dùng để sơn bề mặt ngoài của bồn chứa xăng là:
\[\frac{{10,12\pi }}{8} \approx \frac{{10,12 \cdot 3,14}}{8} \approx 4\,\,\left( {kg} \right)\].
Vậy ta chọn phương án D.
Câu 14:
Một dụng cụ gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình vẽ dưới đây.
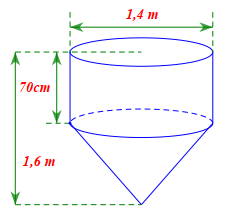
Thể tích của dụng cụ ấy bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi \[{V_1},{r_1},{h_1}\] lần lượt là thể tích, bán kính đáy, chiều cao của phần hình trụ.
\[{V_2},{r_2},{h_2}\] lần lượt là thể tích, bán kính đáy, chiều cao của phần hình nón.
Suy ra \[{r_2} = {r_1}.\]
Đổi: \[70{\rm{\;cm}} = 0,7{\rm{\;m}}.\]
Bán kính đáy của phần hình trụ, hình nón là: \[{r_1} = {r_2} = \frac{{1,4}}{2} = 0,7{\rm{\;(m)}}{\rm{.}}\]
Thể tích của phần hình trụ là:
\[{V_1} = \pi r_1^2{h_1} = \pi \cdot 0,{7^2} \cdot 0,7 = 0,343\pi {\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Chiều cao của phần hình nón là: \[{h_2} = 1,6 - 0,7 = 0,9{\rm{\;(m)}}{\rm{.}}\]
Thể tích của phần hình nón là:
\[{V_2} = \frac{1}{3}\pi r_2^2{h_2} = \frac{1}{3}\pi \cdot 0,{7^2} \cdot 0,9 = 0,147\pi {\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Thể tích của dụng cụ đã cho là:
\[V = {V_1} + {V_2} = 0,343\pi + 0,147\pi = 0,49\pi {\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Vậy ta chọn phương án C.
Câu 15:
Một hình cầu có bán kính \[3{\rm{\;cm}}.\] Một hình nón cũng có bán kính đáy bằng \[3{\rm{\;cm}}\] và có diện tích toàn phần bằng diện tích mặt cầu. Chiều cao của hình nón bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
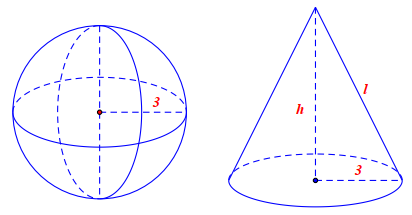
Diện tích mặt cầu là:
\[S = 4\pi {R^2} = 4\pi \cdot {3^2} = 36\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Gọi \(r,\,\,h,\,\,l\) lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón.
Công thức tính diện tích toàn phần của hình nón là \[{S_{tp}} = \pi r\left( {l + r} \right){\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Theo bài, ta có: \[\pi r\left( {l + r} \right) = 36\pi \]
Suy ra \[\pi \cdot 3 \cdot \left( {l + 3} \right) = 36\pi \]
Do đó \[l + 3 = \frac{{36\pi }}{{3\pi }} = 12\] nên \[l = 9{\rm{\;(cm)}}{\rm{.}}\]
Ta có \[{l^2} = {h^2} + {r^2}.\] Suy ra \[{h^2} = {l^2} - {r^2} = {9^2} - {3^2} = 72.\] Do đó \[h = 6\sqrt 2 {\rm{\;(cm)}}{\rm{.}}\]
Vậy ta chọn phương án B.
