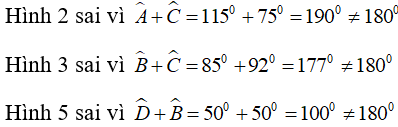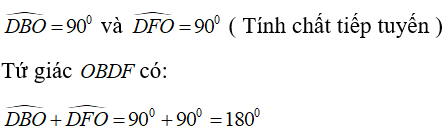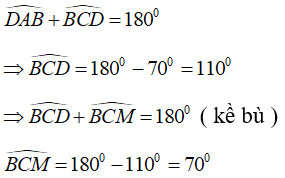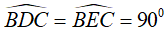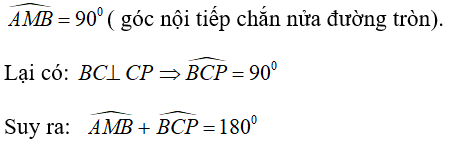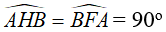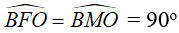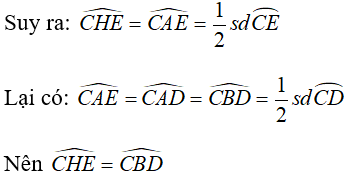Trắc nghiệm Toán 9 Bài 7 (có đáp án): Tứ giác nội tiếp
-
1427 lượt thi
-
10 câu hỏi
-
10 phút
Danh sách câu hỏi
Câu 1:
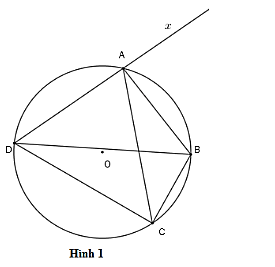
Cho tứ giác ABCD nội tiếp đường tròn (O) (hình 1) . Chọn khẳng định sai?
Xem đáp án
Chọn đáp án D
(góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó )
Phương án A, B, C đúng
Câu 2:
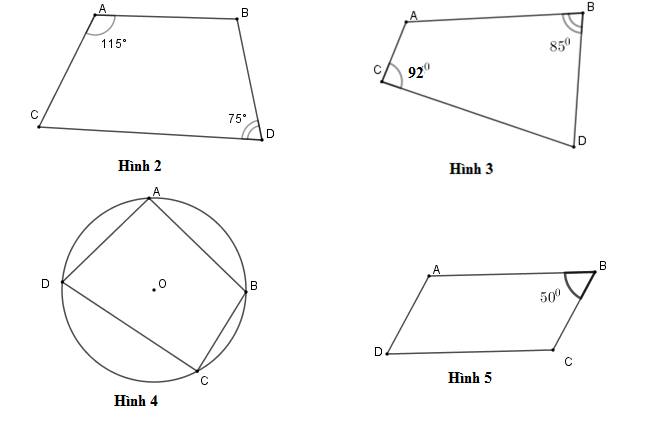
Tứ giác ở hình nào dưới đây là tứ giác nội tiếp?
Xem đáp án
Chọn đáp án C
Hình 4 đúng vì tứ giác này có 4 đỉnh cùng thuộc một đường tròn
Câu 3:
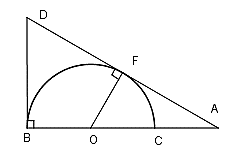
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF và Bx của nửa kia đường tròn (O) ( với F là tiếp điểm ). Tia AF cắt tia Bx của nửa đường tròn tại D. Khi đó tứ giác OBDF là :
Xem đáp án
Chọn đáp án B
Ta có:
Nên nội tiếp được trong một đường tròn
Câu 4:
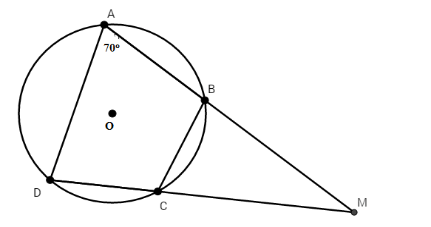
Tứ giác ABCD nội tiếp đường tròn có hai cạnh đối AB và CD cắt nhau tại M và
Xem đáp án
Chọn đáp án C
Tứ giác ABCD nội tiếp nên có :
Câu 5:
Cho tam giác ABC có 2 đường cao BD và CE cắt nhau tại H. Tứ giác nào sau đây là tứ giác nội tiếp
Xem đáp án
Chọn đáp án B.
Ta có: BD và CE là đường cao của tam giác ABC nên 
Trên cùng 1 nửa mặt phẳng bờ BC, hai điểm D và E cùng nhìn đoạn thẳng BC dưới 1 góc vuông nên 4 điểm B, C, D, E cùng thuộc 1 đường tròn hay tứ giác BCDE là tứ giác nội tiếp .
Câu 6:
Cho đường tròn (O) có AB là đường kính. Trên tia đối của tia AB lấy điểm C nằm ngoài đường tròn. Lấy điểm M bất kì nằm trên đường tròn (O). Gọi P là giao điểm của MB và đường vuông góc với AB tại C. Chọn khẳng định đúng.
Xem đáp án
Chọn đáp án A.
Ta có:
Nên
Do đó, tứ giác PMAC là tứ giác nội tiếp
Câu 7:
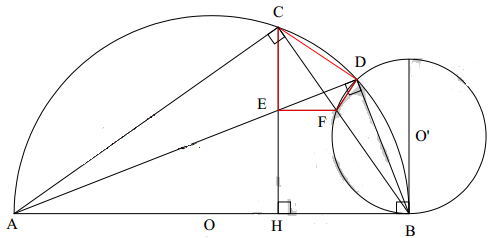
Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E (khác với điểm A). Tiếp tuyến kẻ từ điểm E cắt các tiếp tuyến kẻ từ điểm A và B của nửa đường tròn (O) lần lượt tại C và D. Gọi M là tiếp điểm của tiếp tuyến kẻ từ điểm E. Tìm khẳng định sai
Xem đáp án
Chọn đáp án D.
Suy ra OMDB là tứ giác nội tiếp.
Theo giả thiết ta có:
Suy ra CA // DB
Do đó tứ giác ACDB là hình thang
mà có
Vậy ACDB là hình thang vuông.
Vậy đáp án A, B, C đúng và D sai.
Câu 8:
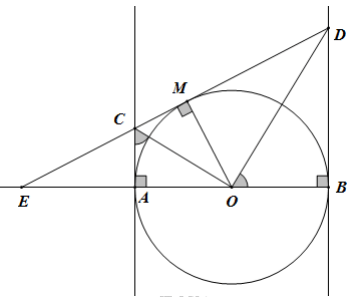
Cho nửa đường tròn (O) đường kính AB, trên nửa đường tròn lấy điểm C (C không trùng với A, B). Gọi H là hình chiếu của C trên đường thẳng AB. Trên cung CB lấy điểm D (D khác C, B), Hai đường thẳng AD và CH cắt nhau tại E. . Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B. Đường tròn (O’) cắt CB tại F khác B.
Chọn khẳng định sai ?
Xem đáp án
Chọn đáp án D
* Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B.
Đường tròn (O’) cắt CB tại F khác B. Chứng minh .
Ta có:
Hai góc ở vị trí đồng vị
Vậy đáp án A, B và C đều đúng nên D sai.
Câu 9:
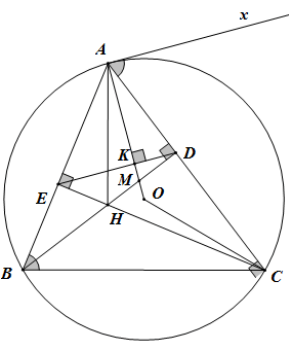
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi H là giao điểm hai đường cao BD và CE của tam giác ABC (D ∈ AC, E ∈ AB). ) Đường thẳng AO cắt ED và BD lần lượt tại K và M. Tìm khẳng định đúng nhất?
Xem đáp án
Chọn đáp án D.
* Chứng minh tứ giác ADHE nội tiếp trong một đường tròn.
Trong nửa mặt phẳng bờ AC không chứa điểm B, vẽ tia tiếp tuyến Ax với đường tròn (O)
Câu 10:
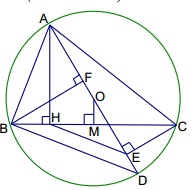
Cho tam giác ABC (AB < AC) có 3 góc nhọn nội tiếp trong đường tròn (O; R). Vẽ đường cao AH của tam giác ABC, đường kính AD của đường tròn. Gọi E, F lần lượt là chân đường vuông góc kẻ từ C và B xuống đường thẳng AD. M là trung điểm của BC.
Tìm khẳng định sai ?
Xem đáp án
Chọn đáp án D
* Chứng minh các tứ giác ABHF và BMFO nội tiếp.
- Từ giả thiết suy ra: 
=> H và F thuộc đường tròn đường kính AB (quỹ tích cung chứa góc)
Vậy tứ giác ABHF nội tiếp đường tròn đường kính AB
- M là trung điểm của BC (gt), suy ra: OM ⊥ BC
Khi đó: 
Nên M, F thuộc đường tròn đường kính OB(quỹ tích cung chứa góc).
Vậy tứ giác BMOF nội tiếp đường tròn đường kính OB
* Chứng minh HE // BD.
Dễ chứng minh tứ giác ACEH nội tiếp đường tròn đường kính AC.
Và chúng ở vị trí đồng vị suy ra: HE // BD