25 câu hỏi trắc nghiệm thuộc Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 2)

Câu 1:

Cho hai biểu thức:

$A = \frac{2 \sqrt{x}}{\sqrt{x} + 3} + \frac{\sqrt{x} + 1}{\sqrt{x} - 3} + \frac{3 - 11 \sqrt{x}}{9 - x}$ và $B = \frac{\sqrt{x} - 3}{\sqrt{x} + 5}$ với $x \geq 0; x \neq 9.$

1) Tính giá trị của biểu thức B khi x = 49

2) Rút gọn biểu thức A

3) Tìm tất cả các giá trị của x để P = AB có giá trị là một số nguyên.

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 2:

Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Lúc 7 giờ sáng, một ca nô xuôi dòng sông từ bến A đến bến B dải 36 km. Khi đến bến B, ca nô nghỉ 30 phút. Sau đó, ca nô lại ngược dòng từ bến B về đến bến A lúc 10 giờ 48 phút cùng ngày. Tính vận tốc riêng của ca nô, biết vận tốc dòng nước là 2 km/h

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 3:

Một quả bóng đá tiêu chuẩn thường được sử dụng tại các giải thi đấu có diện tích bề mặt là $484 π {cm}^{2} .$ Coi quả bóng đá có dạng hình cầu, tính thể tích của quả bóng (làm tròn kết quả đến một chữ số thập phân và lấy $π \approx 3, 140) .$

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 4:

Giải hệ phương trình sau:

\{\begin{cases} \frac{30}{x + 1} - 4 |y - 1| = 22 \\ \frac{9}{x + 1} + 6 |y - 1| = 21 \end{cases} .

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 5:

Trong mặt phẳng với hệ tọa độ Oxy cho parabol $(P) : y = x^{2}$ và đường thẳng y = 5xx - m - 1 với m là tham số.

a) Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt.

b) Tìm tất cả các giá trị của m đề (d) cắt (P) tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$ là các số tự nhiên.

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 6:

Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB tới (O), (A, B là các tiếp điểm). Gọi H là giao điểm của AB với MO; E và F là các giao điểm của đường thẳng MO với đường tròn (O) (với ME < MF)

1) Chứng minh bốn điểm M, A, O, B cùng thuộc một đường tròn.

2) Chứng minh $M O ⊥ A B$ và HE.HF = HM.HO

3) Kẻ đường kính BP của đường tròn (O). Đường thẳng MP cắt đường tròn (O) tại điểm N (N khác P) Gọi I là trung điểm của đoạn thẳng MH. Chứng minh $\hat{M H N} = \hat{M P O}$ và ba điểm A, N, I thẳng hàng.

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 7:

Xét các số thực không âm a, b thỏa mãn

a^{2} + b^{2} = 1.

Tìm giá trị nhỏ nhất của biểu thức

P = a + 2 b + \sqrt{1 + b (b - a)} .

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 8:

Căn bậc hai số học của 81 là

A. 9.

B. \[ - 9.\]

C. $ \pm 9.$

D. \[6\,\,561.\]

Xem đáp án

Đáp án đúng là: A

Căn bậc hai số học của 81 là 9 vì ${9^2} = 81.$

Câu 9:

Trong mặt phẳng tọa độ \[Oxy,\] cho điểm $C\left( {2\,;\,\,4} \right)$ thuộc đồ thị $\left( P \right)$ của hàm số $y = a{x^2},$ với $a \ne 0.$ Điểm $C'$ đối xứng với điểm $C$ qua trục tung \[Oy.\] Khẳng định nào sau đây là đúng?

A. Điểm $C'\left( {2\,;\, - 4} \right)$ và $C' \notin \left( P \right)$.

B. Điểm $C'\left( { - 2\,;\,4} \right)$ và $C' \in \left( P \right)$.

C. Điểm $C'\left( { - 2\,;\,4} \right)$ và $C' \notin \left( P \right)$.

D. Điểm $C'\left( {4\,;\, - 2} \right)$ và $C' \in \left( P \right)$.

Xem đáp án

Đáp án đúng là: B

Đồ thị hàm số $y = a{x^2},$ với $a \ne 0$ đối xứng qua trục $Oy$ nên điểm $C'$ đối xứng với điểm $C$ qua trục tung \[Oy\] thì $C' \in \left( P \right)$ và ${x_{C'}} = - {x_C};\,\,{y_{C'}} = {y_C}$ nên $C'\left( { - 2\,;\,4} \right)$.

Câu 10:

Trong các phương trình sau, phương trình bậc hai một ẩn là

A. ${x^2}\sqrt 2 + 3x - 2 = 0$.

B. $2{x^2} + 3\sqrt x - 2 = 0$.

C. ${x^2} \cdot \sqrt 2 + \frac{3}{x} - 2 = 0$.

D. ${x^2} \cdot \sqrt 2 + 3x - \frac{2}{{{x^2}}} = 0$.

Xem đáp án

Đáp án đúng là: A

Phương trình bậc hai một ẩn có dạng $a{x^2} + bx + c = 0$ với $a \ne 0.$

Do đó phương trình bậc hai một ẩn trong các phương án ở trên là ${x^2}\sqrt 2 + 3x - 2 = 0$.

Câu 11:

Cho $a$ và $b$ là hai số thực tuỳ ý sao cho $a < b$. Khẳng định nào sau đây là đúng?

A. $ - 2025a + 1 < - 2025b + 2$.

B. $2025a + 1 > 2025b + 2$.

C. $ - 2025a < - 2025b - 2$.

D. $2025a + 1 < 2025b + 2$.

Xem đáp án

Đáp án đúng là: D

Vì $a < b$ nên $2025a < 2025b$, suy ra $2025a + 1 < 2025b + 1 < 2025b + 2$.

Vậy ta chọn phương án D.

Câu 12:

Cặp số $\left( {x\,;\,\,y} \right)$ nào dưới đây là nghiệm của hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{3x - 2y = 6}\\{2x + 3y = 10,5}\end{array}} \right.$?

A. $\left( {\frac{3}{2}\,;\,3} \right)$.

B. $\left( {3\,;\,\frac{3}{2}} \right)$.

C. $\left( {3\,;\,\frac{2}{3}} \right)$.

D. $\left( {\frac{2}{3}\,;\,3} \right)$.

Xem đáp án

Đáp án đúng là: B

Sử dụng máy tính cầm tay, ta lần lượt bấm các phím

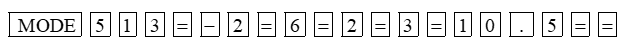
$Cặp số $\left( {x\,;\,\,y} \right)$ nào dưới đây là nghiệm của hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{3x - 2y = 6}\\{2x + 3y = 10,5}\end{array}} \right.$? A. $\left( {\frac{3}{2}\,;\,3} \right)$. B. $\left( {3\,;\,\frac{3}{2}} \right)$. C. $\left( {3\,;\,\frac{2}{3}} \right)$. D. $\left( {\frac{2}{3}\,;\,3} \right)$. (ảnh 1)$

Trên màn hình hiện lên kết quả $x = 3;$ ấn tiếp phím = màn hình hiện kết quả $y = \frac{3}{2}.$

Vậy nghiệm của hệ phương trình đã cho là $\left( {3;\,\,\frac{3}{2}} \right).$ Ta chọn phương án B.

Câu 13:

Trong các khẳng định sau, khẳng định nào đúng?

A. Đường tròn có vô số tâm đối xứng và chỉ có một trục đối xứng.

B. Đường tròn chỉ có một tâm đối xứng và có vô số trục đối xứng.

C. Đường tròn chỉ có một tâm đối xứng và một trục đối xứng.

D. Đường tròn có vô số tâm đối xứng và vô số trục đối xứng.

Xem đáp án

Đáp án đúng là: B

Đường tròn có một tâm đối xứng và có vô số trục đối xứng.

Câu 14:

Cho hình vuông \[MNPQ\] (Hình 1). Phép quay thuận chiều tâm $O$ biến điểm $M$ thành điểm $Q$ thì các điểm \[N,\,\,P,\,\,Q\] tương ứng thành các điểm

$Cho hình vuông \[MNPQ\] (Hình 1). Phép quay thuận chiều tâm $O$ biến điểm $M$ thành điểm $Q$ thì các điểm \[N,\,\,P,\,\,Q\] tương ứng thành các điểm A. \[P,{\rm{ }}N,\,\,M\]. B. \[M,{\rm{ }}N,{\rm{ }}P\]. C. \[M,{\rm{ }}N,{\rm{ }}P\]. D. \[P,{\rm{ }}M,{\rm{ }}N\]. (ảnh 1)$

A. \[P,{\rm{ }}N,\,\,M\].

B. \[M,{\rm{ }}N,{\rm{ }}P\].

C. \[M,{\rm{ }}N,{\rm{ }}P\].

D. \[P,{\rm{ }}M,{\rm{ }}N\].

Xem đáp án

Đáp án đúng là: C

Do \[MNPQ\] là hình vuông nên $MP \bot NQ,$ do đó $\widehat {MON} = \widehat {NOP} = \widehat {POQ} = \widehat {QOM} = 90^\circ $.

Ta có phép quay thuận chiều tâm $O$ biến điểm $M$ thành điểm $Q$ có góc quay là

$\widehat {MON} + \widehat {NOP} + \widehat {POQ} = 90^\circ + 90^\circ + 90^\circ = 270^\circ .$

Ta thấy $\widehat {NOP} + \widehat {POQ} + \widehat {QOM} = 90^\circ + 90^\circ + 90^\circ = 270^\circ .$

Do đó phép quay thuận chiều $270^\circ $ tâm $O$ biến điểm $N$ thành điểm $M$.

Tương tự, phép quay thuận chiều $270^\circ $ tâm $O$ biến điểm $P,\,\,Q$ lần lượt thành các điểm $N,\,\,P$.

Vậy ta chọn phương án C.

Câu 15:

Cho tam giác \[ABC\] vuông tại \[C.\] Biết $BC = 110\;\,{\rm{m}}\,;\,\,\widehat {BAC} = 20^\circ .$ Độ dài cạnh \[AC\] là

(Đơn vị tính: $m;$ Kết quả làm tròn đến hàng đơn vị).

A. 326.

B. 328.

C. 330.

D. 302.

Xem đáp án

$Cho tam giác \[ABC\] vuông tại \[C.\] Biết $BC = 110\;\,{\rm{m}}\,;\,\,\widehat {BAC} = 20^\circ .$ Độ dài cạnh \[AC\] là A. 326. B. 328. C. 330. D. 302. (Đơn vị tính: $m;$ Kết quả làm tròn đến hàng đơn vị). (ảnh 1)$

Câu 16:

Từ điểm $M$ nằm ngoài đường tròn tâm $O$, kẻ hai tiếp tuyến \[MA,{\rm{ }}MB\] \[\left( {A,\,\,B} \right.\] là các tiếp điểm). Nếu $AM = 4\,\,{\rm{cm}}\,{\rm{;}}\,\,\widehat {AMB} = 60^\circ $ thì

A. $BM = 4\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 60^\circ $.

B. $BM = 8\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 30^\circ $.

C. $BM = 4\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 30^\circ $.

D. $BM = 8\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 60^\circ $.

Xem đáp án

$Từ điểm $M$ nằm ngoài đường tròn tâm $O$, kẻ hai tiếp tuyến \[MA,{\rm{ }}MB\] \[\left( {A,\,\,B} \right.\] là các tiếp điểm). Nếu $AM = 4\,\,{\rm{cm}}\,{\rm{;}}\,\,\widehat {AMB} = 60^\circ $ thì A. $BM = 4\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 60^\circ $. B. $BM = 8\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 30^\circ $. C. $BM = 4\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 30^\circ $. D. $BM = 8\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 60^\circ $. (ảnh 1)$

Câu 17:

Một doanh nghiệp sản xuất thùng bằng tôn có dạng hình trụ với hai đáy (Hình 2).

Hình trụ đó có đường kính đáy khoảng \[59{\rm{ cm}}\] và chiều cao khoảng \[91{\rm{ cm}}.\] Chi phí để sản xuất thùng tôn đó là \[100\,\,000\] đồng $/{{\rm{m}}^2}.$ Số tiền mà doanh nghiệp cần chi để sản xuất \[1\,\,000\] thùng tôn là

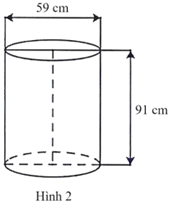
(Đơn vị tính: Đồng. Lấy $\pi \approx 3,14,$ làm tròn kết quả đến hàng nghìn).

A. \[323\,\,238\,\,000.\]

B. \[223\,\,238\,\,000.\]

C. \[123\,\,238\,\,000.\]

D. Đáp án khác.

Xem đáp án

Đáp án đúng là: B

Bán kính đáy của thùng tôn có dạng hình trụ là $R = \frac{{59}}{2} = 29,5{\rm{\;(cm)}}{\rm{.}}$

Diện tích toàn phần của thùng tôn đó là:

${S_{tp}} = {S_{xq}} + 2{S_{day}} = 2\pi \cdot 29,5 \cdot 91 + 2 \cdot \pi \cdot 29,{5^2} = 7\,\,109,5\pi \approx 7\,\,109,5 \cdot 3,14 = 22\,\,323,83{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}$

Đổi \[22\,\,323,83{\rm{\;c}}{{\rm{m}}^2} = 2,232383{\rm{\;}}{{\rm{m}}^2}.\]

Số tiền mà doanh nghiệp cần chi để sản xuất \[1\,\,000\] thùng tôn là:

$\left( {2,232383 \cdot 100\,\,000} \right) \cdot 1\,\,000 \approx 223\,\,238\,\,000$ (đồng).

Câu 18:

Bạn Lan gieo đồng thời hai đồng xu cân đối và đồng chất và quan sát mặt xuất hiện của đồng xu, thì không gian mẫu nhận được là

A. \[\left( {S,\,S} \right);\,\,\left( {S,\,N} \right);\,\,\left( {N,\,S} \right);\,\,\left( {N,\,N} \right)\].

B. $\left( {S,S} \right);\,\,\left( {N,N} \right)$.

C. $\left( {S,N} \right);\,\,\left( {N,S} \right)$.

D. $\left( {S,\,S} \right);\,\,\left( {S,\,N} \right);\,\,\left( {N,\,S} \right)$.

Xem đáp án

Đáp án đúng là: A

Xét phép thử “Gieo đồng thời hai đồng xu cân đối và đồng chất và quan sát mặt xuất hiện của đồng xu”.

Không gian mẫu của phép thử là: $\Omega = \left\{ {\left( {S,\,S} \right);\,\,\left( {S,\,N} \right);\,\,\left( {N,\,S} \right);\,\,\left( {N,\,N} \right)} \right\}.$

Câu 19:

Gieo một con xúc xắc 50 lần cho kết quả như bảng sau:

Số chấm xuất hiện	1	2	3	4	5	6
Tần số	8	7	?	8	6	11

Tần số tương đối xuất hiện của mặt 3 chấm là

A. $20\% $.

B. $10\% $.

C. $8\% $.

D. $6\% $.

Xem đáp án

Đáp án đúng là: A

Tần số xuất hiện mặt 3 chấm là: $50 - 8 - 7 - 8 - 6 - 11 = 10.$

Tần số tương đối xuất hiện của mặt 3 chấm là: $f = \frac{{10}}{{50}} \cdot 100\% = 20\% $.

Câu 20:

Một trường trung học cơ sở mua 500 quyển vở bao gồm $x$ quyển vở loại thứ nhất và $y$ quyển vở loại thứ hai $\left( {x,y \in \mathbb{N}*} \right)$ để làm phần thưởng cho học sinh. Giá bán của mỗi quyển vở loại thứ nhất, loại thứ hai lần lượt là \[8\,\,000\] đồng và \[9\,\,000\] đồng. Biết tổng số tiền nhà trường đã dùng để mua 500 quyển vở đó là \[4\,\,200\,\,000\] đồng. Mỗi học sinh Xuất sắc được thưởng 02 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai; mỗi học sinh Giỏi được thưởng 01 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai; các học sinh khác không được thưởng và số học sinh này chiếm $40\% $ tổng số học sinh cả trường.

a) $x + y = 500$.

b) $9x + 8y = 4\,\,200\,\,000$.

c) $x = 300;y = 200$.

d) Tổng số học sinh của trường trung học cơ sở đó là 600 học sinh.

Xem đáp án

Đáp án: a) Đúng; b) Sai; c) Đúng; d) Sai.

a) Tổng số quyển vở đã mua là 500 quyển nên $x + y = 500$.

b) Tổng số tiền nhà trường mua 500 quyển vở là 4 200 000 đồng nên $8\,\,000x + 9\,\,000y = 4\,\,200\,\,000$ hay $8x + 9y = 4\,\,200$

c) Ta có hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{x + y = 500}\\{8x + 9y = 4\,\,200.}\end{array}} \right.$

Sử dụng máy tính cầm tay giải hệ phương trình (1) ta được $\left\{ {\begin{array}{*{20}{l}}{x = 300}\\{y = 200}\end{array}} \right.$ (thỏa mãn điều kiện).

d) Gọi $u,\,\,v$ lần lượt là số học sinh Xuất sắc và số học sinh Giỏi $\left( {u,\,\,v \in {\mathbb{N}^*}} \right)$.

Mỗi học sinh Xuất sắc được thưởng 02 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai nên ta có phương trình $2u + v = 300.$

Mỗi học sinh Giỏi được thưởng 01 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai nên ta có phương trình $u + v = 200.$

Ta có hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{2u + v = 300}\\{u + v = 200}\end{array}} \right.$ (2).

Sử dụng máy tính cầm tay giải hệ phương trình (2) ta được $\left\{ {\begin{array}{*{20}{l}}{u = 100}\\{v = 100}\end{array}} \right.$ (thỏa mãn điều kiện).

Vậy có tổng $100 + 100 = 200$ học sinh Xuất sắc và Giỏi, chiếm $40\% $ tổng số học sinh cả trường.

Do đó, tổng số học sinh của trường là $200:40\% = 500$ (học sinh).

Câu 21:

Một chiếc áo có giá niêm yết là \[120\,\,000\] đồng. Để thanh lí chiếc áo, đầu tiên người ta giảm giá $x\% $ so với giá niêm yết. Do vẫn chưa bán được chiếc áo nên người ta tiếp tục giảm giá $x\% $ so với giá vừa được giảm. Sau hai đợt giảm giá, giá của chiếc áo còn \[76\,\,800\] đồng.

a) Giá của chiếc áo sau lần giảm giá thứ nhất là: $120\,\,000 - 1200x$ (đồng).

b) Giá của chiếc áo sau hai lần giảm giá là: $12{x^2} - 2\,\,400x + 120\,\,000$ (đồng).

c) Theo bài, sau hai đợt giảm giá, giá của chiếc áo còn \[76\,\,800\] đồng nên ta có phương trình ${x^2} - 200x + 3\,\,600 = 0$.

d) $x = 180$.

Xem đáp án

Đáp án: a) Đúng; b) Đúng; c) Sai; d) Sai.

a) Giá của chiếc áo sau lần giảm giá thứ nhất là $120\,\,000 - 120\,\,000 \cdot x\% = 120\,\,000 - 1\,\,200x$ (đồng).

b) Giá của chiếc áo sau hai lần giảm giá là:

$\left( {120\,\,000 - 1\,\,200x} \right) - \left( {120\,\,000 - 1\,\,200x} \right) \cdot x\% $

$ = 120\,\,000 - 1\,\,200x - 1\,\,200x + 12{x^2}$

$ = 12{x^2} - 2\,\,400x + 120\,\,000$ (đồng).

c) Theo bài, sau hai đợt giảm giá, giá của chiếc áo còn \[76\,\,800\] đồng nên ta có phương trình $12{x^2} - 2\,\,400x + 120\,\,000 = 76\,\,800$ hay $12{x^2} - 2\,\,400x + 43\,\,200 = 0$.

d) Giải phương trình ta được hai nghiệm ${x_1} = 180$ (không thỏa mãn) và ${x_2} = 20$ (thỏa mãn).

Vậy $x = 20$.

Lưu ý: $0 < x < 100$.

Câu 22:

Người ta muốn dựng một khung cổng hình vuông \[ABCD\] có độ dài cạnh bằng \[3{\rm{ cm}}\] được bao bởi một khung thép có dạng nửa đường tròn tâm $F$ bán kính \[FA\] (như hình 3).

Người ta muốn dựng một khung cổng hình vuông ABCD có độ dài cạnh bằng 3cm được bao bởi một khung thép có dạng nửa đường tròn tâm F bán kínhFA (như hình 3). (ảnh 1)

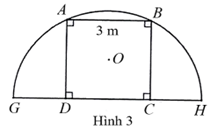
a) Độ dài đoạn thẳng \[OA\] là $1,5\sqrt 2 \;\,{\rm{m}}$.

b) Độ dài đoạn thẳng $HG = 3\sqrt 5 \;\,{\rm{m}}$.

c) Độ dài cung \[GAH\] là $3\sqrt 5 \pi \,\,{\rm{m}}$.

d) Người ta muốn sơn toàn bộ nửa hình tròn (không sơn phần cổng \[ABCD).\] Giá tiền sơn $30\,\,000$ đồng${\rm{/}}{{\rm{m}}^{\rm{2}}}{\rm{.}}$ Biết $\pi = 3,14$ kết quả làm tròn đến nghìn đồng. Số tiền sơn là \[1\,\,059\] (nghìn đồng).

Xem đáp án

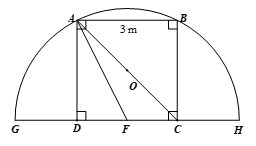
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Sai.

a) Ta có \[ABCD\] là hình vuông nên $\widehat {ABC} = \widehat {ADC} = 90^\circ $ và $BC = CD = AD = AB = 3{\rm{\;m}}$.

Xét $\Delta ABC$ vuông tại $B$, theo định lí Pythagore, ta có:

$A{C^2} = A{B^2} + A{C^2} = {3^2} + {3^2} = 18.$

Suy ra $AC = \sqrt {18} = 3\sqrt 2 {\rm{\;(m)}}{\rm{.}}$

Do đó $AO = \frac{1}{2}AC = \frac{1}{2} \cdot 3\sqrt 2 = 1,5\sqrt 2 {\rm{\;(m)}}{\rm{.}}$

b) Ta có $F$ là trung điểm của $CD$ nên $FD = FC = \frac{1}{2}DC = \frac{1}{2} \cdot 3 = 1,5{\rm{\;(m)}}{\rm{.}}$

Xét $\Delta ADF$ vuông tại $D$, theo định lí Pythagore, ta có:

$F{A^2} = A{D^2} + D{F^2} = {3^2} + 1,{5^2} = 11,25$.

Suy ra $FA = \sqrt {11,25} = 1,5\sqrt 5 {\rm{\;(m)}}{\rm{.}}$

Do đó $HG = 2FA = 2 \cdot 1,5\sqrt 5 = 3\sqrt 5 {\rm{\;(m)}}{\rm{.}}$

c) Độ dài cung \[GAH\] là $\pi \cdot FA = \pi \cdot 1,5\sqrt 5 = 1,5\sqrt 5 \pi {\rm{\;(m)}}{\rm{.}}$

d) Diện tích cần sơn là $\frac{1}{2}\pi \cdot F{A^2} - {S_{ABCD}} = \frac{1}{2} \cdot 3,14 \cdot {\left( {1,5\sqrt 5 } \right)^2} - {3^2} = 8,6625{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}$

Số tiền sơn là $8,6625 \cdot 30\,\,000 \approx 260\,\,000$ (đồng).

Câu 23:

Một hộp chứa 15 quả cầu màu xanh được đánh số từ 1 đến 15 và 5 quả cầu màu đỏ được đánh số từ 16 đến 20. Lấy ngẫu nhiên một quả cầu trong hộp.

a) Xác suất để lấy được quả cầu màu xanh bằng xác suất để lấy được quả cầu màu đỏ.

b) Xác suất để lấy được quả cầu ghi số chẵn là \[0,5.\]

c) Xác suất để lấy ra quả cầu có màu xanh và ghi số lẻ là \[0,4.\]

d) Xác suất để lấy ra quả cầu màu đỏ hoặc ghi số chẵn là \[0,8.\]

Xem đáp án

Đáp án: a) Sai; b) Đúng; c) Đúng; d) Sai.

a) Xác suất lấy được quả cầu màu xanh là $\frac{{15}}{{20}} = 0,75$.

Xác suất lấy được quả cầu màu đỏ là $\frac{5}{{20}} = 0,25$.

Ta thấy $0,75 \ne 0,25$ nên khẳng định a) là sai.

b) Trong 20 quả cầu, có 10 quả cầu ghi số chẵn là: \[2;\,\,4;\,\,6;\,\,8;\,\,10;\,\,12;\,\,14;\,\,16;\,\,18;\,\,20.\]

Xác suất lấy được quả cầu ghi số chẵn là $\frac{{10}}{{20}} = 0,5$.

c) Trong 20 quả cầu, có $8$ quả cầu màu xanh và ghi số lẻ là: $1;\,\,3;\,\,5;\,\,7;\,\,9;\,\,11;\,\,13;\,\,15$.

Xác suất lấy ra quả cầu màu xanh và ghi số lẻ là $\frac{8}{{20}} = 0,4$.

d) Trong 20 quả cầu, có $12$ quả cầu màu đỏ hoặc ghi số chẵn là: $2;\,\,4;\,\,6;\,\,8;\,\,10;\,\,12;\,\,14;\,\,16;\,\,17;\,\,18;\,\,19;\,\,20.$

Xác suất lấy ra quả cầu màu đỏ hoặc ghi số chẵn là $\frac{{12}}{{20}} = 0,6$.

Câu 24:

Nước từ vòi phun nước (đặt cách mặt nước \[0,2{\rm{ m)}}\] được phun lên cao sẽ đạt một độ cao nào đó rồi rơi xuống. Giả sử nước được từ đầu vòi phun (vị trí \[A)\] và rơi xuống vị trí $B.$ Đường đi của nước là một phần của parabol dạng $y = - \frac{1}{8}{x^2}$ trong hệ trục tọa độ \[Oxy\] với $O$ là điểm cao nhất của nước được phun ra so với mặt nước, trục \[Ox\] song song với \[AB,{\rm{ }}x\] và $y$ tính bằng đơn vị mét. Biết $AB = 12\;\,{\rm{m}}\,{\rm{.}}$ Tính chiều cao $h$ từ điểm $O$ đến mặt nước (Hình 5).

Nước từ vòi phun nước (đặt cách mặt nước 0,2m được phun lên cao sẽ đạt một độ cao nào đó rồi rơi xuống. Giả sử nước được từ đầu vòi phun (vị trí A] và rơi (ảnh 1)

Xem đáp án

Đáp số: $4,7{\rm{\;m}}.$

Đồ thị hàm số $y = - \frac{1}{8}{x^2}$ đối xứng qua trục $Oy,$ do đó $A,\,\,B$ đối xứng với nhau qua trục $Oy.$

Gọi $H$ là giao điểm của \[AB\] và \[Oy,\] khi đó ta có $H$ là trung điểm của $AB$ nên \[BH = \frac{1}{2}AB = 6{\rm{\;(m)}}{\rm{.}}\]

Thay $x = 6$ vào hàm số $y = - \frac{1}{8}{x^2}$, ta được $y = - \frac{1}{8} \cdot {6^2} = - 4,5$.

Vậy chiều cao từ điểm $O$ đến mặt nước là \[\left| { - 4,5} \right| + 0,2 = 4,7{\rm{\;(m)}}{\rm{.}}\]

Câu 25:

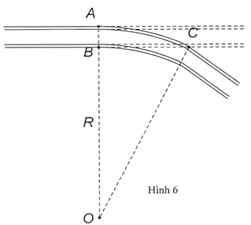
Để giúp tàu hỏa chuyển từ đường ray theo hướng này sang đường ray theo hướng khác người ta làm một đoạn đường ray hình vòng cung (hình 6). Biết độ rộng của đường ray là $AB \approx 1,1\;\,{\rm{m}}$ và đoạn $BC \approx 28,4\,\;{\rm{m}}$. Hãy tính bán kính $R = OA$ của đoạn đường ray hình vòng cung. (Tính bằng đơn vị: $m,$ làm tròn đến hàng đơn vị).

Để giúp tàu hỏa chuyển từ đường ray theo hướng này sang đường ray theo hướng khác người ta làm một đoạn đường ray hình vòng cung (hình 6). Biết độ rộng (ảnh 1)

Xem đáp án

Ta có $OA = OC = R;\,\,OB = R - 1,1{\rm{\;(m)}}{\rm{.}}$

Áp dụng định lí Pythagore vào tam giác $OBC$ vuông tại $B$, ta có:

$O{C^2} = O{B^2} + B{C^2}$ hay ${R^2} \approx {\left( {R - 1,1} \right)^2} + 28,{4^2}$

Hay ${R^2} \approx {R^2} - 2,2R + 1,21 + 806,56$

Do đó $ - 2,2R + 807,77 \approx 0$

Suy ra $R \approx 367{\rm{\;(m)}}{\rm{.}}$