8 câu hỏi trắc nghiệm thuộc Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 10)

Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 10)

Đề số 1

Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 10)

126 lượt thi
8 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho parabol (P): y = x² và đường thẳng (d): y = -x + 2.

a) Vẽ (P) và (d) trên cùng hệ trục toạ độ.

b) Tìm toạ độ giao điểm của (P) và (d) bằng phép tính.

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 2:

Cho phương trình 3x² + 5x - 1 = 0 có hai nghiệm. Không giải phương trình hãy tính giá trị của biểu thức

A = (3 x_{1} - 2 x_{2}) (3 x_{2} - 2 x_{1}) - 2023

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 3:

Để ước tính chiều cao tối đa của trẻ em khi đạt đến độ trưởng thành, hoàn toàn có thể dựa vào chiều cao của bố mẹ. Cách tính chiều cao của con theo bố mẹ được các chuyên gia đánh giá cao bởi thực tế, sự di truyền các thế hệ có ảnh hưởng nhất định đến chiều cao của trẻ. Ta có công thức tính như sau: $C = (B + M + 13 A) : 2$ .

Trong đó: A là chiều cao của người con (cm);

B là chiều cao của người bố (cm);

M là chiều cao của người mẹ (cm);

A = 1 khi người con có giới tính là Nam;

A = -1 khi người con có giới tính là Nữ.

a) Em hãy dùng công thức trên để tìm chiều cao tối đa của bạn Nam (giới tính là nam) biết ba của bạn Nam có chiều cao là 175 cm và mẹ của bạn Nam có chiều cao là 168 cm

b) Bạn Hương (giới tính là nữ) có chiều cao là 164 cm Em hãy tính xem chiều cao tối đa của mẹ bạn Hương khi biết chiều cao của ba bạn Hương là 180 cm

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 4:

Một hãng hàng không quy định xử phạt hành lý kí gửi vượt quá quy định miễn phí (hành lý quá cước). Cứ vượt quá x (kg) hành lý thì khách hàng phải trả tiền phạt y (USD). Người ta thấy mối quan hệ giữa hai đại lượng này là một hàm số bậc nhất y = ax + b có đồ thị như hình vẽ bên.

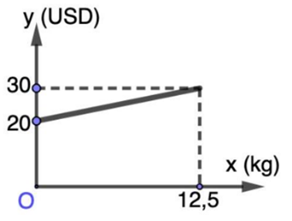
a) Xác định các hệ số a và b.

b) Hãy tính số tiền phạt của một hành khách có 20kg hành lý quá cước.

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 5:

Đầu mỗi tháng ông Mạnh gửi vào ngân hàng 2 000 000 đồng với lãi suất 0,65%/tháng và không rút gốc, lãi tháng trước. Sau 3 tháng thì số tiền ông Mạnh nhận được cả gốc lẫn lãi (sau khi ngân hàng đã tính lãi tháng cuối cùng) là bao nhiêu?

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 6:

Để đo chiều cao một ngọn đồi, người ta đặt giác kế tại hai vị trí là A (chân toà nhà) và B (sân thượng toà nhà). Thông qua giác kế người ta đo được góc

\hat{C A H} = 45 °

và

\hat{C B E} = 30 °

. Tính độ cao của ngọn đồi? Biết toà nhà cao 50 m (kết quả làm tròn đến hàng đơn vị).

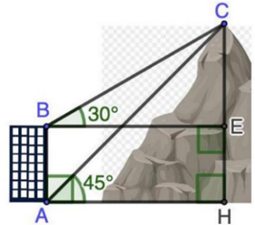
Để đo chiều cao một ngọn đồi, người ta đặt giác kế tại hai vị trí là A (chân toà nhà) và B (sân thượng toà nhà). Thông qua giác kế người ta đo được góc (ảnh 1)

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 7:

Bánh xe đạp bơm căng có đường kính là 73 cm

a) Hỏi xe đạp đi được bao nhiêu km nếu bánh xe quay được 1000 vòng? Kết quả làm tròn đến chữ số thập phân thứ ba.

b) Hỏi bánh xe quay được bao nhiêu vòng khi xe đi được 4,64 km (kết quả làm tròn đến hàng đơn vị)?

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 8:

Cho $Δ A B C$ nhọn (AB < AC) nội tiếp đường tròn (O;R) có hai đường cao BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại Y và X. Kẻ đường kính AK của (O), HK cắt (O) tại P.

a) Chứng minh: tứ giác APFE nội tiếp đường tròn.

b) Chứng minh: PB.PE = PC.PF.

c) Gọi M là điểm chính giữa của cung nhỏ BC, MX và MY cắt AB, AC lần lượt tại I và J. Chứng minh: H, I, J thẳng hàng.

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Bắt đầu thi ngay