Trắc nghiệm Toán 9 Kết nối tri thức Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Trắc nghiệm Toán 9 Kết nối tri thức Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
323 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất hai ẩn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình \(0x - 0y = 5\) không phải là phương trình bậc nhất hai ẩn do \[a,{\rm{ }}b\] đồng thời bằng 0.
Câu 2:
Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất hai ẩn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình  không phải là phương trình bậc nhất hai ẩn do
không phải là phương trình bậc nhất hai ẩn do 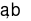 đồng thời bằng 0.
đồng thời bằng 0.
Câu 3:
Hệ số \(a,\,\,b,\,\,c\) tương ứng của phương trình bậc nhất hai ẩn \(x + 2y - 1 = 0\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình bậc nhất hai ẩn \(x + 2y - 1 = 0\) nên \(a = 1;\,\,b = 2;\,\,c = - 1\).
Câu 4:
Hệ số 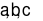 tương ứng của phương trình bậc nhất hai ẩn
tương ứng của phương trình bậc nhất hai ẩn  là
là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình bậc nhất hai ẩn  nên
nên 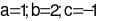 .
.
Câu 5:
Cặp số nào sau đây là nghiệm của phương trình \(2x - y - 1 = 0\)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
⦁ Thay \(x = 0\) và \(y = 1\) vào phương trình \(2x - y - 1 = 0\) ta được \(2 \cdot 0 - 1 - 1 = - 2 \ne 0\).
Do đó \(\left( {0;\,\,1} \right)\) không phải là nghiệm phương trình đã cho.
⦁ Thay \(x = 1\) và \(y = 0\) vào phương trình \(2x - y - 1 = 0\) ta được \(2 \cdot 1 - 0 - 1 = 1 \ne 0\).
Do đó \(\left( {1;\,\,0} \right)\) không phải là nghiệm phương trình.
⦁ Thay \(x = 1\) và \(y = 1\) vào phương trình \(2x - y - 1 = 0\) ta được \(2 \cdot 1 - 1 - 1 = 0\).
Do đó \(\left( {1;\,\,1} \right)\) là nghiệm phương trình đã cho.
⦁ Thay \(x = - 1\) và \(y = 0\) vào phương trình \(2x - y - 1 = 0\) ta được \(2 \cdot \left( { - 1} \right) - 0 - 1 = - 3 \ne 0\).
Do đó \(\left( { - 1;\,\,0} \right)\) không phải là nghiệm phương trình đã cho.
Vậy ta chọn phương án C.
Câu 6:
Cặp số nào sau đây là nghiệm của phương trình  ?
?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
⦁ Thay 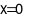 và
và  vào phương trình
vào phương trình  ta được
ta được 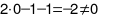 .
.
Do đó 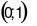 không phải là nghiệm phương trình đã cho.
không phải là nghiệm phương trình đã cho.
⦁ Thay 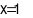 và
và  vào phương trình
vào phương trình  ta được
ta được 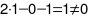 .
.
Do đó 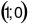 không phải là nghiệm phương trình.
không phải là nghiệm phương trình.
⦁ Thay 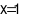 và
và  vào phương trình
vào phương trình  ta được
ta được 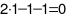 .
.
Do đó  là nghiệm phương trình đã cho.
là nghiệm phương trình đã cho.
⦁ Thay 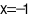 và
và  vào phương trình
vào phương trình  ta được
ta được  .
.
Do đó 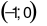 không phải là nghiệm phương trình đã cho.
không phải là nghiệm phương trình đã cho.
Vậy ta chọn phương án C.
Câu 7:
Trong các hệ phương trình sau, hệ nào không phải là hệ phương trình bậc nhất hai ẩn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta thấy hệ phương trình \[\left\{ \begin{array}{l}{x^2} - 4{y^2} = 0\\3x + 2y = 7\end{array} \right.\] có chứa số hạng có bậc của \(x,\,\,y\) là 2 nên không phải là phương trình bậc nhất hai ẩn.
Câu 8:
Trong các hệ phương trình sau, hệ nào không phải là hệ phương trình bậc nhất hai ẩn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta thấy hệ phương trình 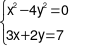 có chứa số hạng có bậc của
có chứa số hạng có bậc của  là 2 nên không phải là phương trình bậc nhất hai ẩn.
là 2 nên không phải là phương trình bậc nhất hai ẩn.
Câu 9:
Cho hệ phương trình \[\left\{ \begin{array}{l}x + y = 0\\x + 3y = 4\end{array} \right.\], cặp số nào sau đây là nghiệm của hệ phương trình đã cho?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
⦁ Thay \(x = 0\) và \(y = 1\) vào phương trình \(x + y = 0\) ta được \(0 + 1 = 1 \ne 0\) nên cặp số \(\left( {0;\,\,1} \right)\) không phải là nghiệm của phương trình \(x + y = 0\). Do đó cặp số \(\left( {0;\,\,1} \right)\) không phải là nghiệm của hệ phương trình đã cho.
⦁ Thay \(x = 2\) và \(y = 2\) vào phương trình \(x + y = 0\) ta được \(2 + 2 = 4 \ne 0\) nên cặp số \(\left( {2;\,\,2} \right)\) không phải là nghiệm của phương trình \(x + y = 0\). Do đó cặp số \(\left( {2;\,\,2} \right)\) không phải là nghiệm của hệ phương trình đã cho.
⦁ Thay \(x = 3\) và \(y = - 3\) vào phương trình \[x + 3y = 4\] ta được \[3 + 3 \cdot \left( { - 3} \right) = - 9 \ne 4\] nên cặp số \(\left( {3;\,\, - 3} \right)\) không phải là nghiệm của phương trình \[x + 3y = 4\]. Do đó cặp số \(\left( {3;\,\, - 3} \right)\) không phải là nghiệm của hệ phương trình đã cho.
⦁ Thay \(x = - 2\) và \(y = 2\) vào từng phương trình của hệ phương trình đã cho, ta được:
\( - 2 + 2 = 0\);
\( - 2 + 3 \cdot 2 = 4\).
Do đó cặp số \(\left( { - 2;\,\,2} \right)\) là nghiệm chung của hai phương trình nên \(\left( { - 2;\,\,2} \right)\) là một nghiệm của hệ phương trình đã cho.
Câu 10:
Cho hệ phương trình  , cặp số nào sau đây là nghiệm của hệ phương trình đã cho?
, cặp số nào sau đây là nghiệm của hệ phương trình đã cho?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
⦁ Thay 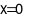 và
và  vào phương trình
vào phương trình  ta được
ta được 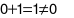 nên cặp số
nên cặp số 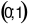 không phải là nghiệm của phương trình
không phải là nghiệm của phương trình  . Do đó cặp số
. Do đó cặp số 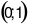 không phải là nghiệm của hệ phương trình đã cho.
không phải là nghiệm của hệ phương trình đã cho.
⦁ Thay  và
và  vào phương trình
vào phương trình  ta được
ta được 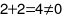 nên cặp số
nên cặp số 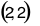 không phải là nghiệm của phương trình
không phải là nghiệm của phương trình  . Do đó cặp số
. Do đó cặp số 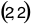 không phải là nghiệm của hệ phương trình đã cho.
không phải là nghiệm của hệ phương trình đã cho.
⦁ Thay  và
và  vào phương trình
vào phương trình 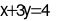 ta được
ta được  nên cặp số
nên cặp số 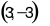 không phải là nghiệm của phương trình
không phải là nghiệm của phương trình 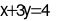 . Do đó cặp số
. Do đó cặp số 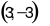 không phải là nghiệm của hệ phương trình đã cho.
không phải là nghiệm của hệ phương trình đã cho.
⦁ Thay  và
và  vào từng phương trình của hệ phương trình đã cho, ta được:
vào từng phương trình của hệ phương trình đã cho, ta được:
 ;
;
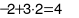 .
.
Do đó cặp số 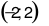 là nghiệm chung của hai phương trình nên
là nghiệm chung của hai phương trình nên 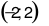 là một nghiệm của hệ phương trình đã cho.
là một nghiệm của hệ phương trình đã cho.
II. Thông hiểu
Câu 11:
Tất cả các nghiệm của phương trình \(2x - 3y = 1\) được biểu diễn bằng đường thẳng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Từ phương trình \(2x - 3y = 1\) ta có \(3y = 2x - 1\) suy ra \[y = \frac{2}{3}x - \frac{1}{3}\]
Do đó, tất cả các nghiệm của phương trình \(2x - 3y = 1\) được biểu diễn bởi đường thẳng \[y = \frac{2}{3}x - \frac{1}{3}.\]
Câu 12:
Tất cả các nghiệm của phương trình  được biểu diễn bằng đường thẳng nào dưới đây?
được biểu diễn bằng đường thẳng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Từ phương trình  ta có
ta có  suy ra
suy ra 
Do đó, tất cả các nghiệm của phương trình  được biểu diễn bởi đường thẳng
được biểu diễn bởi đường thẳng 
Câu 13:
Tất cả các nghiệm của phương trình \(0x + 5y = 2\) được biểu diễn bởi
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Từ phương trình \(0x + 5y = 2\) ta có \(5y = 2\) suy ra \[y = \frac{2}{5}\]
Do đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng \[y = \frac{2}{5}\].
Câu 14:
Tất cả các nghiệm của phương trình  được biểu diễn bởi
được biểu diễn bởi
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Từ phương trình  ta có
ta có  suy ra
suy ra 
Do đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng  .
.
Câu 15:
Tất cả các nghiệm của phương trình \(3x - 0y = 1\) được biểu diễn bởi
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Từ phương trình \(3x - 0y = 1\) ta có \(3x = 1\) suy ra \[x = \frac{1}{3}\]
Do đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đồ thị của hàm số \[x = \frac{1}{3}.\]
Câu 16:
Tất cả các nghiệm của phương trình 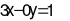 được biểu diễn bởi
được biểu diễn bởi
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Từ phương trình 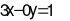 ta có
ta có 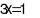 suy ra
suy ra 
Do đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đồ thị của hàm số 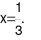
Câu 17:
Giá trị nào của \[{y_0}\] để cặp số \(\left( {1;\,\,{y_0}} \right)\) là nghiệm của phương trình \( - 3x + 2y = 7\)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Để cặp số \(\left( {1;\,\,{y_0}} \right)\) là nghiệm của phương trình \( - 3x + 2y = 7\) thì \(x = 1\) và \(y = {y_0}\) thỏa mãn phương trình \( - 3x + 2y = 7\).
Thay \(x = 1\) và \(y = {y_0}\) vào phương trình đó, ta được:
\( - 3 \cdot 1 + 2{y_0} = 7\) suy ra \(2{y_0} = 10\) nên \({y_0} = 5\).
Câu 18:
Giá trị nào của  để cặp số
để cặp số 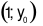 là nghiệm của phương trình
là nghiệm của phương trình  ?
?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Để cặp số 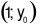 là nghiệm của phương trình
là nghiệm của phương trình  thì
thì 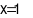 và
và 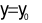 thỏa mãn phương trình
thỏa mãn phương trình  .
.
Thay 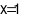 và
và 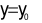 vào phương trình đó, ta được:
vào phương trình đó, ta được:
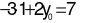 suy ra
suy ra 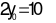 nên
nên 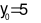 .
.
Câu 19:
Giá trị nào của \[{x_0}\] để cặp số \(\left( {{x_0};\,\,2} \right)\) là nghiệm của phương trình \(2x + y = - 6\)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Để cặp số \(\left( {{x_0};\,\,2} \right)\) là nghiệm của phương trình \(2x + y = - 6\) thì \(x = {x_0}\) và \(y = 2\) phải thỏa mãn phương trình \(2x + y = - 6\).
Thay \(x = {x_0}\) và \(y = 2\) vào phương trình đó, ta được:
\(2{x_0} + 2 = - 6\) suy ra \(2{x_0} = - 8\) nên \({x_0} = - 4\).
Câu 20:
Giá trị nào của  để cặp số
để cặp số  là nghiệm của phương trình
là nghiệm của phương trình 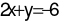 ?
?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Để cặp số  là nghiệm của phương trình
là nghiệm của phương trình 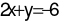 thì
thì 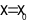 và
và  phải thỏa mãn phương trình
phải thỏa mãn phương trình 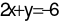 .
.
Thay 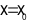 và
và  vào phương trình đó, ta được:
vào phương trình đó, ta được:
 suy ra
suy ra 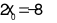 nên
nên  .
.
Câu 21:
Cho biết phương trình \(2x + my = 4\) nhận cặp số \(\left( {0;\,\,1} \right)\) làm nghiệm. Giá trị của \(m\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Do phương trình \(2x + my = 4\) nhận cặp số \(\left( {0;\,\,1} \right)\) làm nghiệm nên \(x = 0\) và \(y = 1\) thỏa mãn phương trình \(2x + my = 4\).
Thay \(x = 0\) và \(y = 1\) vào phương trình đó, ta được:
\(2 \cdot 0 + m \cdot 1 = 4\) suy ra \(m = 4\).
Câu 22:
Cho biết phương trình  nhận cặp số
nhận cặp số 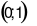 làm nghiệm. Giá trị của
làm nghiệm. Giá trị của  là
là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Do phương trình  nhận cặp số
nhận cặp số 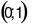 làm nghiệm nên
làm nghiệm nên 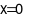 và
và  thỏa mãn phương trình
thỏa mãn phương trình  .
.
Thay 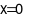 và
và  vào phương trình đó, ta được:
vào phương trình đó, ta được:
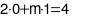 suy ra
suy ra 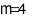 .
.
Câu 23:
Biết phương trình \[mx - 5y + 1 = 0\] nhận cặp số \[\left( {1;2} \right)\] làm nghiệm. Giá trị của \[m\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Do phương trình \[mx - 5y + 1 = 0\] nhận cặp số \[\left( {1;2} \right)\] làm nghiệm nên \[x = 1;\,\,y = 2\] thỏa mãn phương trình \[mx - 5y + 1 = 0\].
Thay \[x = 1;\,\,y = 2\]vào phương trình đó, ta được:
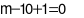
\[m \cdot 1 - 5 \cdot 2 + 1 = 0\]
\[m - 10 + 1 = 0\]
\[m = 9\].
Vậy \[m = 9\].
Câu 24:
Biết phương trình 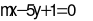 nhận cặp số
nhận cặp số 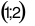 làm nghiệm. Giá trị của
làm nghiệm. Giá trị của  là
là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Do phương trình 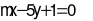 nhận cặp số
nhận cặp số 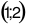 làm nghiệm nên
làm nghiệm nên  thỏa mãn phương trình
thỏa mãn phương trình 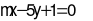 .
.
Thay  vào phương trình đó, ta được:
vào phương trình đó, ta được:
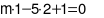
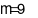 .
.
Vậy 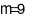 .
.
III. Vận dụng
Câu 25:
Cho phương trình \[3x + \left( {{m^2} + m} \right)y = 6\] có nghiệm \[\left( { - 2;6} \right)\]. Có bao nhiêu giá trị \(m\) thỏa mãn điều kiện trên?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Thay \[x = - 2,y = 6\] vào phương trình đã cho, ta được:
\[3 \cdot \left( { - 2} \right) + \left( {{m^2} + m} \right) \cdot 6 = 6\].
Giải phương trình:
\[3 \cdot \left( { - 2} \right) + \left( {{m^2} + m} \right) \cdot 6 = 6\]
\[6\left( {{m^2} + m} \right) = 12\]
\[{m^2} + m = 2\]
\({m^2} + m - 2 = 0\)
\({m^2} - m + 2m - 2 = 0\)
\(m\left( {m - 1} \right) + 2\left( {m - 1} \right) = 0\)
\(\left( {m - 1} \right)\left( {m + 2} \right) = 0\)
\(m - 1 = 0\) hoặc \(m + 2 = 0\)
\(m = 1\) hoặc \(m = - 2\)
Vậy có hai giá trị \(m\) thỏa mãn yêu cầu đề bài.
Do đó ta chọn phương án C.
Câu 26:
Cho phương trình 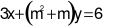 có nghiệm
có nghiệm 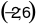 . Có bao nhiêu giá trị
. Có bao nhiêu giá trị  thỏa mãn điều kiện trên?
thỏa mãn điều kiện trên?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Thay 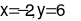 vào phương trình đã cho, ta được:
vào phương trình đã cho, ta được:
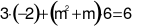 .
.
Giải phương trình:
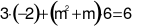


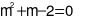

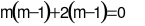
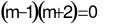
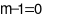 hoặc
hoặc 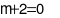
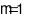 hoặc
hoặc 
Vậy có hai giá trị  thỏa mãn yêu cầu đề bài.
thỏa mãn yêu cầu đề bài.
Do đó ta chọn phương án C.
Câu 27:
Phương trình \[3x - 2y = 1\] luôn nhận cặp số nào sau đây là nghiệm khi \[m\] thay đổi?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
⦁ Xét phương án A: Thay \[x = 3m - 1,y = 2m - 1\] vào phương trình đã cho, ta được:
\[3 \cdot \left( {3m - 1} \right) - 2 \cdot \left( {2m - 1} \right) = 5m - 1 \ne 1.\]
Do đó cặp số \[\left( {3m - 1;2m - 1} \right)\] không là nghiệm của phương trình đã cho khi \[m\] thay đổi.
⦁ Tương tự, ta thay các cặp \(\left( {x;\,\,y} \right)\) ở phương án B, D vào phương trình đã cho ta thấy rằng cặp số đó không phải là nghiệm của phương trình này khi \[m\] thay đổi.
⦁ Thay \[x = 2m + 1,y = 3m + 1\] vào phương trình đã cho, ta được:
\[3 \cdot \left( {2m + 1} \right) - 2 \cdot \left( {3m + 1} \right) = 6m + 3 - 6m - 2 = 1.\]
Do đó cặp số \[\left( {2m + 1;3m + 1} \right)\] là nghiệm của phương trình đã cho khi \[m\] thay đổi.
Vậy ta chọn phương án C.
Câu 28:
Phương trình 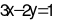 luôn nhận cặp số nào sau đây là nghiệm khi
luôn nhận cặp số nào sau đây là nghiệm khi  thay đổi?
thay đổi?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
⦁ Xét phương án A: Thay 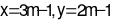 vào phương trình đã cho, ta được:
vào phương trình đã cho, ta được:
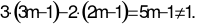
Do đó cặp số 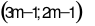 không là nghiệm của phương trình đã cho khi
không là nghiệm của phương trình đã cho khi  thay đổi.
thay đổi.
⦁ Tương tự, ta thay các cặp  ở phương án B, D vào phương trình đã cho ta thấy rằng cặp số đó không phải là nghiệm của phương trình này khi
ở phương án B, D vào phương trình đã cho ta thấy rằng cặp số đó không phải là nghiệm của phương trình này khi  thay đổi.
thay đổi.
⦁ Thay  vào phương trình đã cho, ta được:
vào phương trình đã cho, ta được:
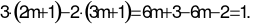
Do đó cặp số 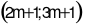 là nghiệm của phương trình đã cho khi
là nghiệm của phương trình đã cho khi  thay đổi.
thay đổi.
Vậy ta chọn phương án C.
Câu 29:
Để chuẩn bị cho buổi liên hoan của gia đình, bác Thu mua hai loại thực phẩm là thịt bò và thịt lợn. Giá tiền thịt bò là 250 nghìn đồng/kg, giá tiền thịt lợn là 150 nghìn đồng/kg. Bác Ngọc đã chi 500 nghìn để mua \[3,5\] kg hai loại thực phẩm trên. Gọi \[x\] và \[y\] lần lượt là số kilôgam thịt bò và thịt lợn mà bác Thu đã mua. Hệ phương trình bậc nhất hai ẩn biểu diễn mối quan hệ giữa \[x\] và \[y\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo bài, bác Thu chỉ mua \[3,5\] kg thịt bò và thịt lợn nên ta có phương trình: \(x + y = 3,5\).
Do giá tiền thịt bò là 250 nghìn đồng/kg nên số tiền bác Thu chi ra để mua \(x\) kilôgam thịt bò là: \(250x\) (nghìn đồng).
Do giá tiền thịt lợn là 150 nghìn đồng/kg nên số tiền bác Thu chi ra để mua \(y\) kilôgam thịt lợn là: \(150y\) (nghìn đồng).
Theo bài, bác Thu đã chi 500 nghìn để mua hai loại thực phẩm trên nên ta có phương trình:
\(250x + 150y = 500\).
Vậy ta có hệ phương trình \[\left\{ \begin{array}{l}x + y = 3,5\\250x + 150y = 500\end{array} \right.\].
Câu 30:
Để chuẩn bị cho buổi liên hoan của gia đình, bác Thu mua hai loại thực phẩm là thịt bò và thịt lợn. Giá tiền thịt bò là 250 nghìn đồng/kg, giá tiền thịt lợn là 150 nghìn đồng/kg. Bác Ngọc đã chi 500 nghìn để mua 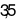 kg hai loại thực phẩm trên. Gọi
kg hai loại thực phẩm trên. Gọi 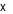 và
và 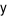 lần lượt là số kilôgam thịt bò và thịt lợn mà bác Thu đã mua. Hệ phương trình bậc nhất hai ẩn biểu diễn mối quan hệ giữa
lần lượt là số kilôgam thịt bò và thịt lợn mà bác Thu đã mua. Hệ phương trình bậc nhất hai ẩn biểu diễn mối quan hệ giữa 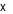 và
và 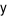 là
là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo bài, bác Thu chỉ mua 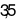 kg thịt bò và thịt lợn nên ta có phương trình:
kg thịt bò và thịt lợn nên ta có phương trình: 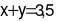 .
.
Do giá tiền thịt bò là 250 nghìn đồng/kg nên số tiền bác Thu chi ra để mua 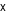 kilôgam thịt bò là:
kilôgam thịt bò là: 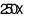 (nghìn đồng).
(nghìn đồng).
Do giá tiền thịt lợn là 150 nghìn đồng/kg nên số tiền bác Thu chi ra để mua 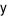 kilôgam thịt lợn là:
kilôgam thịt lợn là: 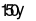 (nghìn đồng).
(nghìn đồng).
Theo bài, bác Thu đã chi 500 nghìn để mua hai loại thực phẩm trên nên ta có phương trình:
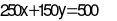 .
.
Vậy ta có hệ phương trình 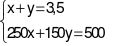 .
.
