22 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 6 - vietjack.online

Bài tập theo tuần Toán 9 - Tuần 6

Đề số 1

Bài tập theo tuần Toán 9 - Tuần 6

475 lượt thi
22 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Sắp xếp theo thứ tự giảm dần:

$\sin 27^{0}, \cos 78^{0}, \sin 19^{0}, \cos 68^{0}, \sin 54^{0}, \cos 50^{0}$

Ta có

$\begin{array}{l} \cos 78^{0} = \sin 12^{0}; \cos 68^{0} = \sin 22^{0}, \cos 50^{0} = \sin 40^{0} \\ \Rightarrow \sin 54^{0} > \sin 40^{0} > \sin 27^{0} > \sin 22^{0} > \sin 19^{0} > \sin 12^{0} \\ h a y \sin 54^{0} > \cos 50^{0} > \sin 27^{0} > \cos 68^{0} > \sin 19^{0} > \cos 68^{0} \end{array}$

Câu 2:

Cho $Δ A B C$ có $A B = 9 c m, A C = 12 c m, B C = 15 c m,$ AH là đường cao.

a) Chứng minh $Δ A B C$ vuông

b b) Tính BH, CH

c) Chứng minh $\sqrt{B H . H C} \leq \frac{B C}{2}$

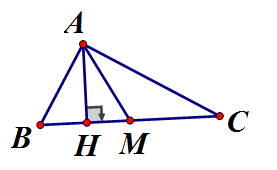
Cho tam giác ABC có AB = 9cm, AC = 12cm, BC = 15cm, AH là đường cao. (ảnh 1)

a) Ta có:

B C^{2} = 15^{2} = 225

;

A B^{2} + A C^{2} = 9^{2} + 12^{2} = 225 \Rightarrow B C^{2} = A B^{2} + A C^{2}

$\Rightarrow B C^{2} = A B^{2} + A C^{2} \Rightarrow Δ A B C$ vuông tại A (định lý Pytago đảo)

b b) Áp dụng hệ thức lượng vào $Δ A B C$ vuông tại A, đường cao AH

\Rightarrow A B^{2} = B H . B C \Rightarrow B H = \frac{A B^{2}}{B C} = \frac{9^{2}}{15} = 5, 4 (c m) \Rightarrow H C = 9, 6 c m

c c) $B H . H C = A H^{2}$ . Gọi M là trung điểm BC mà $A H \leq A M = \frac{1}{2} B C$ (tính chất đường trung tuyến) $\Rightarrow B H . H C \leq {(\frac{1}{2} B C)}^{2} \Rightarrow B H . H C \leq \frac{1}{4} B C^{2}$ . Dấu "=" xảy ra $\Leftrightarrow H \equiv M$

Câu 3:

Cho $Δ A B C$ vuông tại A, có $A B = 5 c m, A C = 12 c m .$ Giải tam giác ABC.

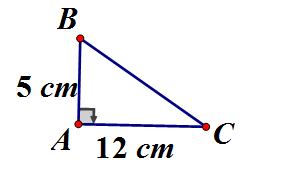
Cho tam giác ABC vuông tại A, có AB = 5cm, AC = 12cm. Giải tam giác ABC. (ảnh 1)

Áp dụng định lý Pytago vào $Δ A B C$ vuông tại A, ta có:

\begin{array}{l} B C^{2} = A B^{2} + A C^{2} \Rightarrow B C = \sqrt{5^{2} + 12^{2}} = 13 (c m) \\ \sin ​ B = \frac{A C}{B C} = \frac{12}{13} \Rightarrow \hat{B} = 67^{0} \Rightarrow \hat{C} = 90^{0} - 67^{0} = 23^{0} \end{array}

Vậy

B C = 13 c m, \hat{B} = 67^{0}, \hat{C} = 22^{0}

Câu 4:

Cho $Δ A B C$ có đường trung tuyến AM bằng cạnh AC.

Chứng minh rằng : $\tan B = \frac{1}{3} \tan C$

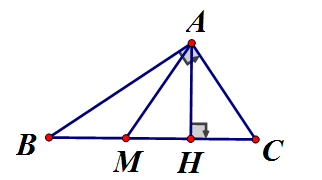
Cho tam giác ABC có đường trung tuyến AM bằng cạnh AC. Chứng minh rằng (ảnh 1)

Vẽ đường cao $A H, d o Δ A M C$ cân tại A nên AH đường cao cũng là đường trung tuyến

\Rightarrow M H = H C = \frac{1}{2} M C \Rightarrow M C = 2 M H = 2 C H \Rightarrow B H = 3 H C

$Δ H A B$ vuông tại H $\Rightarrow \tan B = \frac{A H}{B H}$

$Δ H A C$ vuông tại H $\Rightarrow \tan C = \frac{A H}{H C} \Rightarrow \tan B = \frac{1}{3} \tan C$

Câu 5:

Δ A B C

\hat{A} = 60^{0} .

Chứng minh rằng:

B C^{2} = A B^{2} + A C^{2} - A B . A C

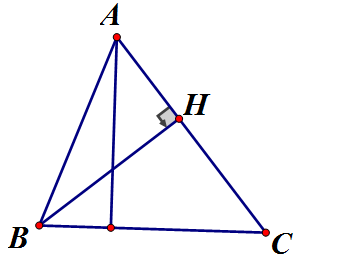
Cho tam giác ABC nhọn có góc A = 60 độ. Chứng minh rằng: (ảnh 1)

Vẽ $B H ⊥ A C \Rightarrow Δ A H B$ nửa đều và $Δ B H C$ vuông tại H

\Rightarrow B C^{2} = A H^{2} + H C^{2} = (A B^{2} - A H^{2}) + {(A C - A H)}^{2}

\Rightarrow B C^{2} = A B^{2} - A H^{2} + A C^{2} - 2. A C . A H + A H^{2}

B C^{2} = A B^{2} + A C^{2} - 2. A C . A H

$B C^{2} = A B^{2} + A C^{2} - A B . A C$ (do $Δ B H C$ nửa đều nên AB = 2AH) (đpcm)

Câu 6:

Cho $Δ M N P$ vuông tại M, MH là đường cao, MN = 16cm, MP = 30cm.

a) Giải tam giác vuông (độ dài lấy 2 chữ số thập phân, góc làm tròn đến phút)

b) Tính NH, PH

c) Phân giác ND của $\hat{N} (D \in M H) .$ Tính MD, DH

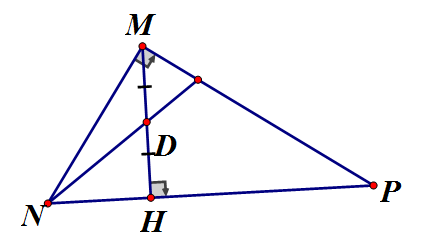
Cho tam giác MNP vuông tại M, MH là đường cao, MN = 16cm, MP = 30cm. (ảnh 1)

a a) Áp dụng định lý Pytago vào $Δ M N P$ vuông tại M

$\Rightarrow N P = \sqrt{M N^{2} + N P^{2}} = \sqrt{16^{2} + 30^{2}} = 34 (c m)$

$\sin N = \frac{M P}{N P} = \frac{30}{34} \Rightarrow \hat{N} \approx 62^{0} \Rightarrow \hat{P} = 90^{0} - \hat{N} = 90^{0} - 62^{0} = 28^{0}$

b) Áp dụng hệ thức lượng trong tam giác vuông $\Rightarrow N H . N P = N M^{2}$

Hay $N H .34 = 16^{2} \Rightarrow N H = \frac{128}{17} (c m) \Rightarrow P H = 34 - \frac{128}{17} = \frac{450}{17} (c m)$

c) $Δ M N H$ có ND là phân giác $\Rightarrow \frac{M D}{D H} = \frac{M N}{N H}$ , áp dụng tính chất dãy tỉ số bằng nhau $\Rightarrow \frac{D H + M D}{D H} = \frac{N H + M N}{N H} \Rightarrow \frac{M H}{D H} = \frac{N H + M N}{N H} (*)$

Ta có: $M H = \sqrt{N H . H P}$ (hệ thức lượng) $\Rightarrow M H = \frac{240}{17} (c m)$ . Thay vào (*)

Vậy $D H = \frac{384}{85} c m, M D = \frac{48}{5} c m$

Câu 7:

Cho biểu thức

B = \frac{a \sqrt{a} - 1}{a - \sqrt{a}} - \frac{a \sqrt{a} + 1}{a + \sqrt{a}} + (1 - \frac{1}{\sqrt{a}}) (\frac{\sqrt{a} + 1}{\sqrt{a} - 1} + \frac{\sqrt{a} - 1}{\sqrt{a} + 1})

a) Tìm ĐKXĐ – Rút gọn B

b) Tìm a để B = 7

$\begin{array}{l} B = \frac{a \sqrt{a} - 1}{a - \sqrt{a}} - \frac{a \sqrt{a} + 1}{a + \sqrt{a}} + (1 - \frac{1}{\sqrt{a}}) (\frac{\sqrt{a} + 1}{\sqrt{a} - 1} + \frac{\sqrt{a} - 1}{\sqrt{a} + 1}) \\ = \frac{(\sqrt{a} - 1) (a + \sqrt{a} + 1)}{\sqrt{a} . (\sqrt{a} - 1)} - \frac{(\sqrt{a} + 1) (a - \sqrt{a} + 1)}{\sqrt{a} . (\sqrt{a} + 1)} + \frac{\sqrt{a} - 1}{\sqrt{a}} . [\frac{{(\sqrt{a} + 1)}^{2} + {(\sqrt{a} - 1)}^{2}}{(\sqrt{a} - 1) (\sqrt{a} + 1)}] \\ = \frac{a + \sqrt{a} + 1 - a + \sqrt{a} - 1}{\sqrt{a}} + \frac{\sqrt{a} - 1}{\sqrt{a}} . \frac{2 \sqrt{a} + 2}{(\sqrt{a} - 1) (\sqrt{a} + 1)} \\ = \frac{2 \sqrt{a}}{\sqrt{a}} + \frac{2 (\sqrt{a} + 1)}{\sqrt{a} . (\sqrt{a} + 1)} = 2 + \frac{2}{a} = \frac{2 \sqrt{a} + 2}{\sqrt{a}} \end{array}$

$b) B = 7 \Rightarrow 2 \sqrt{a} + 2 = 7 \sqrt{a} \Leftrightarrow 5 \sqrt{a} = 2 \Rightarrow a = \frac{4}{25} (t m)$

Câu 8:

P = (3 + \frac{x - 2 \sqrt{x}}{\sqrt{x} - 2}) (3 - \frac{3 x + \sqrt{x}}{3 \sqrt{x} + 1})

a) Rút gọn P

b) Tính giá trị của P khi

x = \sqrt{6 + 2 \sqrt{5}} - \sqrt{6 - 2 \sqrt{5}}

$\begin{array}{l} a) P = (3 + \frac{x - 2 \sqrt{x}}{\sqrt{x} - 2}) . (3 - \frac{3 x + \sqrt{x}}{3 \sqrt{x} + 1}) \\ = [3 + \frac{\sqrt{x} (\sqrt{x} - 2)}{\sqrt{x} - 2}] . [3 - \frac{\sqrt{x} . (3 \sqrt{x} + 1)}{3 \sqrt{x} + 1}] = (3 + \sqrt{x}) (3 - \sqrt{x}) = 9 - x \\ b) x = \sqrt{6 + 2 \sqrt{5}} - \sqrt{6 - 2 \sqrt{5}} = \sqrt{{(\sqrt{5} + 1)}^{2}} - \sqrt{{(\sqrt{5} - 1)}^{2}} \\ = \sqrt{5} + 1 - \sqrt{5} + 1 = 2 \Rightarrow P = 9 - x = 7 \end{array}$

Câu 9:

Cho biểu thức

P = (\frac{4 a}{\sqrt{a} - 1} - \frac{\sqrt{a}}{a - \sqrt{a}}) . \frac{\sqrt{a} - 1}{a^{2}}

a) Rút gọn biểu thức P

b) Với giá trị nào của a thì P = 3

$a) P = (\frac{4 a}{\sqrt{a} - 1} - \frac{\sqrt{a}}{a - \sqrt{a}}) . \frac{\sqrt{a} - 1}{a^{2}} (\begin{array}{l} a > 0 \\ a \neq 1 \end{array}) = \frac{4 a - 1}{\sqrt{a} - 1} . \frac{\sqrt{a} - 1}{a^{2}} = \frac{4 a - 1}{a^{2}}$

$\begin{array}{l} b) P = 3 \Leftrightarrow \frac{4 a - 1}{a^{2}} = 3 \Leftrightarrow 3 a^{2} - 4 a + 1 = 0 \\ \Leftrightarrow 3 a^{2} - 4 a + 1 = 0 \Leftrightarrow 3 a^{2} - 3 a - a + 1 = 0 \\ \Leftrightarrow 3 a (a - 1) - (a - 1) = 0 \\ \Leftrightarrow (a - 1) (3 a - 1) = 0 \Rightarrow [\begin{array}{l} a = 1 (k t m) \\ a = \frac{1}{3} (t m) \end{array} \end{array}$

Vậy $a = \frac{1}{3}$ thì P = 3

Câu 10:

Giải phương trình:

\sqrt{4 x^{2} - 4 x + 1} - \sqrt{9 x^{2}} = 0

\begin{array}{l} \sqrt{4 x^{2} - 4 x + 1} - \sqrt{9 x^{2}} = 0 \\ \Leftrightarrow \sqrt{{(2 x - 1)}^{2}} - \sqrt{{(3 x)}^{2}} = 0 \\ \Leftrightarrow |2 x - 1| = |3 x| \\ \Leftrightarrow [\begin{array}{l} 2 x - 1 = 3 x \\ 2 x - 1 = - 3 x \end{array} \Rightarrow [\begin{array}{l} x = - 1 \\ x = \frac{1}{5} \end{array} \end{array}

Câu 11:

Giải phương trình:

\sqrt{3 x - 5} + \sqrt{2 x - 3} = \sqrt{x + 2}

\begin{array}{l} \sqrt{3 x - 5} + \sqrt{2 x - 3} = \sqrt{x + 2} (x \geq \frac{5}{3}) \\ \Leftrightarrow \sqrt{3 x - 5} = \sqrt{x + 2} - \sqrt{2 x - 3} \\ \Rightarrow 3 x - 5 = x + 2 + 2 x - 3 - 2 \sqrt{(x + 2) (2 x - 3)} \\ \Leftrightarrow \sqrt{(x + 2) (2 x - 3)} = 2 \Leftrightarrow 2 x^{2} + x - 6 = 4 \\ \Leftrightarrow 2 x^{2} + x - 10 = 0 \Leftrightarrow [\begin{array}{l} x = 2 (t m) \\ x = - \frac{5}{2} (k t m) \end{array} \end{array}

Câu 12:

Giải phương trình:

\frac{2 x^{2}}{3 - \sqrt{{(9 + 2 x)}^{2}}} = x + 9

$\frac{2 x^{2}}{3 - \sqrt{{(9 + 2 x)}^{2}}} = x + 9 \Leftrightarrow \frac{2 x^{2}}{3 - |9 + 2 x|} = x + 9$

$\begin{array}{l} x \geq \frac{- 9}{2} \Rightarrow \frac{2 x^{2}}{3 - 9 - 2 x} = x + 9 \\ \Leftrightarrow 2 x^{2} + 24 x = - 54 + 2 x^{2} \\ \Rightarrow x = - \frac{9}{4} (t m) \\ x < - \frac{9}{2} \Rightarrow \frac{2 x^{2}}{3 + 9 + 2 x} = x + 9 \\ \Leftrightarrow 2 x^{2} = 2 x^{2} + 30 x + 108 \\ \Rightarrow x = - \frac{- 18}{5} (k t m) V a y x = \frac{- 9}{4} \end{array}$

Câu 13:

Giải phương trình:

\sqrt{x + 4} + \sqrt{x - 1} = 2

\begin{array}{l} x + 4 + x - 1 + 2 \sqrt{(x + 4) (x - 1)} = 2 \\ \Leftrightarrow 4 (x + 4) (x - 1) = {(- 2 x - 1)}^{2} \\ \Leftrightarrow 4 x^{2} + 12 x - 16 = 4 x^{2} + 4 x + 1 \\ \Leftrightarrow x = \frac{17}{8} (t m) \end{array}

Câu 14:

Tính

$\sqrt{44} - \sqrt{176} + 2 \sqrt{275}$

$\sqrt{44} - \sqrt{176} + 2 \sqrt{275} = 2 \sqrt{11} - 4 \sqrt{11} + 10 \sqrt{11} = 8 \sqrt{11}$

Câu 15:

Tính

$5 \sqrt{3} - 3 \sqrt{48} + 2 \sqrt{75} - \frac{1}{3} \sqrt{108}$

$5 \sqrt{3} - 3 \sqrt{48} + 2 \sqrt{75} - \frac{1}{3} \sqrt{108} = 5 \sqrt{3} - 12 \sqrt{3} + 10 \sqrt{3} - 2 \sqrt{3} = \sqrt{3}$

Câu 16:

Tính

$\sqrt{343} - \sqrt{112} - \sqrt{63} - \sqrt{21}$

$\sqrt{343} - \sqrt{112} - \sqrt{63} - \sqrt{21} = 7 \sqrt{7} - 4 \sqrt{7} - 3 \sqrt{7} - \sqrt{21} = - \sqrt{21}$

Câu 17:

Tính

$\sqrt{6 + 2 \sqrt{2} . \sqrt{3 - \sqrt{4 + 2 \sqrt{3}}}}$

\begin{array}{l} \sqrt{6 + 2 \sqrt{2} . \sqrt{3 - \sqrt{4 + 2 \sqrt{3}}}} = \sqrt{6 + 2 \sqrt{2} . \sqrt{3 - (\sqrt{3} + 1)}} \\ = \sqrt{6 + 2 \sqrt{2} . \sqrt{2 - \sqrt{3}}} = \sqrt{6 + 2 \sqrt{4 - 2 \sqrt{3}}} \\ = \sqrt{6 + 2 (\sqrt{3} - 1)} = \sqrt{6 + 2 \sqrt{3} - 2} \\ = \sqrt{4 + 2 \sqrt{3}} = \sqrt{{(\sqrt{3} + 1)}^{2}} = \sqrt{3} + 1 \end{array}

Câu 18:

Tính

$\sqrt{28 + \sqrt{300}} + \sqrt{19 - \sqrt{192}}$

$\begin{array}{l} \sqrt{28 + \sqrt{300}} + \sqrt{19 - \sqrt{192}} \\ = \sqrt{28 + 10 \sqrt{3}} + \sqrt{19 - 8 \sqrt{3}} \\ = \sqrt{5^{2} + 2.5. \sqrt{3} + {(\sqrt{3})}^{2}} + \sqrt{4^{2} - 2.4. \sqrt{3} + {(\sqrt{3})}^{2}} \\ = \sqrt{{(5 + \sqrt{3})}^{2}} + \sqrt{{(4 - \sqrt{3})}^{2}} \\ = 5 + \sqrt{3} + 4 - \sqrt{3} = 9 \end{array}$

Câu 19:

Tính

\begin{array}{l} \frac{\sqrt{7} + \sqrt{5}}{\sqrt{7} - \sqrt{5}} + \frac{\sqrt{7} - \sqrt{5}}{\sqrt{7} + \sqrt{5}} \end{array}

\begin{array}{l} \frac{\sqrt{7} + \sqrt{5}}{\sqrt{7} - \sqrt{5}} + \frac{\sqrt{7} - \sqrt{5}}{\sqrt{7} + \sqrt{5}} = \frac{{(\sqrt{7} + \sqrt{5})}^{2} + {(\sqrt{7} - \sqrt{5})}^{2}}{(\sqrt{7} - \sqrt{5}) (\sqrt{7} + \sqrt{5})} \\ = \frac{12 + 2 \sqrt{35} + 12 - 2 \sqrt{35}}{7 - 5} = \frac{24}{2} = 12 \end{array}

Câu 20:

Phân tích đa thức thành nhân tử

a + \sqrt{a} + 2 \sqrt{a b} + 2 \sqrt{b}

$\begin{array}{l} a + \sqrt{a} + 2 \sqrt{a b} + 2 \sqrt{b} \\ = \sqrt{a} (\sqrt{a} + 1) + 2 \sqrt{b} (\sqrt{a} + 1) \\ = (\sqrt{a} + 1) (\sqrt{a} + 2 \sqrt{b}) \end{array}$

Câu 21:

Phân tích đa thức thành nhân tử

{(1 + \sqrt{x})}^{2} - 4 \sqrt{x}

$\begin{array}{l} {(1 + \sqrt{x})}^{2} - 4 \sqrt{x} \\ = 1 + 2 \sqrt{x} + x - 4 \sqrt{x} \\ = x - 2 \sqrt{x} + 1 \\ = {(\sqrt{x} - 1)}^{2} \end{array}$

Câu 22:

Phân tích đa thức thành nhân tử

b \sqrt{b} - 4 b + 4 \sqrt{b} - a \sqrt{b}

\begin{array}{l} b \sqrt{b} - 4 b + 4 \sqrt{b} - a \sqrt{b} \\ = \sqrt{b} [(b - 4 \sqrt{b} + 4) - a] = \sqrt{b} [{(\sqrt{b} - 2)}^{2} - {(\sqrt{a})}^{2}] \\ = \sqrt{b} (\sqrt{b} - 2 - \sqrt{a}) (\sqrt{b} - 2 + \sqrt{a}) \end{array}

Bắt đầu thi ngay

Có thể bạn quan tâm

Các bài thi hot trong chương