24 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 28

Câu 1:

Cho hình vuông có cạnh là 5cm nội tiếp đường tròn (O). Hãy tính chu vi và đường tròn (O) và diện tích hình tròn (O)

Cho hình vuông có cạnh là 5cm nội tiếp đường tròn (O). Hãy tính chu vi và (ảnh 1)

Áp dụng định lý Pytago

\begin{array}{l} \Rightarrow B D = \sqrt{A B^{2} + A D^{2}} = \sqrt{5^{2} + 5^{2}} = 5 \sqrt{2} \\ \Rightarrow R = \frac{B D}{2} = \frac{5 \sqrt{2}}{2} \\ \Rightarrow C h u v i (O) = 2 π R = 2 π . \frac{5 \sqrt{2}}{2} = 5 \sqrt{2} π (c m) \\ S_{(O)} = π R^{2} = π {(\frac{5 \sqrt{2}}{2})}^{2} = \frac{25}{2} π (c m^{2}) \end{array}

Câu 2:

Cho tam giác ABC nội tiếp đường tròn (O; 3cm). Tính diện tích hình quạt tròn giới hạn bởi hai bán kính OA, OC và cung nhỏ AC khi $∠ A B C = 60^{0}$

Xem đáp án

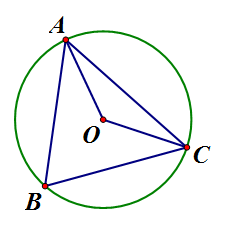
Cho tam giác ABC nội tiếp đường tròn (O; 3cm). Tính diện tích hình quạt tròn (ảnh 1)

S_{q u a t (A O C)} = \frac{π R^{2} n}{360} = \frac{π {.3}^{2} . ∠ A O C}{360^{0}} (1)

Ta có : $∠ A O C = 2 ∠ A B C$ (góc nội tiếp và góc ở tâm cùng chắn 1 cung)

$\Rightarrow ∠ A O C = {2.60}^{0} = 120^{0},$ thay vào (1)

$\Rightarrow S_{q u a t (A O C)} = \frac{π {.9.120}^{0}}{360^{0}} = 3 π (c m^{2})$

Câu 3:

Cho đường tròn (O; R) đường kính AB cố định. Gọi M là trung điểm đoạn OB. Dây CD vuông góc với AB tại M. Điểm E chuyển động trên cung lớn $C D (E \neq A) .$ Nối AE cắt CD tại K. Nối BE cắt CD tại H.

a) Chứng minh 4 điểm B, M, E, K thuộc một đường tròn

b) Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC.

Xem đáp án

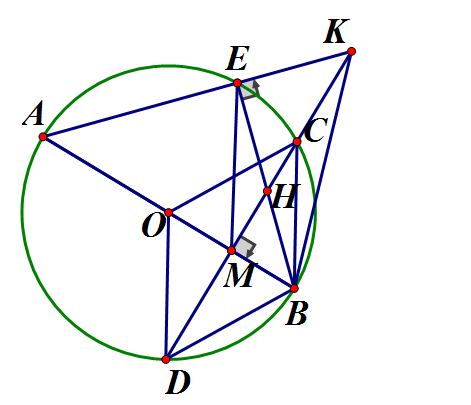
Cho đường tròn (O; R) đường kính AB cố định. Gọi M là trung điểm đoạn OB (ảnh 1)

a) Ta có $∠ A E B = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow ∠ K E B = ∠ K M B = 90^{0} \Rightarrow$ Tứ giác BMEK có đỉnh M, E liên tiếp cùng nhìn BK dưới 1 góc vuông nên BMEK là tứ giác nội tiếp

$\Rightarrow B, M, E, K$ cùng thuộc một đường tròn

b) Ta có $A M ⊥ C D$ tại trung điểm M của CD (tính chất đường kính – dây cung)

$\Rightarrow C O D B$ có hai đường chéo vuông góc tại trung điểm mỗi đường $\Rightarrow C O D B$ là hình thoi

$\Rightarrow O C = C B = O B = R \Rightarrow C O B$ đều

\Rightarrow ∠ C O B = 60^{0} \Rightarrow S_{q u a t (B O C)} = \frac{π R^{2} .60}{360} = \frac{π R^{2}}{6} (d v d t)

Câu 4:

Tính diện tích một hình quạt tròn có bán kính 6cm và số đo cung là $72^{0}$

Xem đáp án

$S_{q u a t} = \frac{π R^{2} n}{360} = \frac{π .6.72}{360} = \frac{6 π}{5} (d v d t)$

Câu 5:

Cho đường tròn (O) bán kính R. Vẽ hai đường kính AB, CD của đường tròn (O) vuông góc với nhau. Trên AO lấy E sao cho $O E = \frac{1}{3} O A,$ tia CE cắt đường tròn (O) tại M

a) Chứng minh tứ giác MEOD nội tiếp đường tròn

b) Tính CE theo R

c) Gọi I là giao điểm của CM và AD. Chứng minh $O I ⊥ A D$

d) Tính diện tích hình tạo bởi dây AD và cung nhỏ AD của đường tròn (O)

Xem đáp án

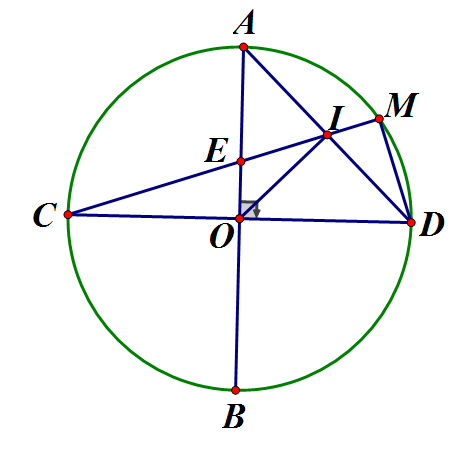
Cho đường tròn (O) bán kính R. Vẽ hai đường kính AB, CD của đường tròn (O) (ảnh 1)

a) Ta có $∠ C M D = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)

Nên tứ giác MEOD có : $∠ O M E + ∠ E O D = 90^{0} + 90^{0} = 180^{0}$

Nên MEOD là tứ giác nội tiếp

B) $O E = \frac{1}{3} O A = \frac{R}{3}$

$Δ C O E$ vuông tại O nên

$C E = \sqrt{C O^{2} + O E^{2}} (P y t a g o) = \sqrt{R^{2} + {(\frac{R}{3})}^{2}} = \frac{R \sqrt{10}}{3}$

c) Xét $Δ C A D$ có AO là đường trung tuyến mà $O E = \frac{1}{3} O A \Rightarrow A E = \frac{2}{3} A O$

$\Rightarrow E$ là trọng tâm $Δ C A D$ $\Rightarrow$ CI lả đường trung tuyến

$\Rightarrow$ I là trung điểm dây $A D \Rightarrow O I ⊥ A D$ (đường kính dây cung)

d) $S_{q u a t (A O D)} = \frac{π R^{2} n}{360} = \frac{π R^{2} {.90}^{0}}{360^{0}} = \frac{π R^{2}}{4} (d v d t)$

Câu 6:

Giải phương trình sau bằng công thức nghiệm thu gọn:

$3 x^{2} - 6 x + 1 = 0$

Xem đáp án

$\begin{array}{l} 3 x^{2} - 6 x + 1 = 0 \\ a = 3, b = - 6, c = 1 \Rightarrow b' = - 3 \\ Δ' = {(- 3)}^{2} - 3.1 = 6 \end{array}$

Nên phương trình có hai nghiệm :

[\begin{array}{l} x_{1} = \frac{3 + \sqrt{6}}{3} \\ x_{2} = \frac{3 - \sqrt{6}}{3} \end{array}

Câu 7:

Giải phương trình sau bằng công thức nghiệm thu gọn:

$x^{2} + 4 \sqrt{3} x + 12 = 0$

Xem đáp án

$\begin{array}{l} x^{2} + 4 \sqrt{3} x + 12 = 0 \\ a = 1, b = 4 \sqrt{3}, c = 12 \Rightarrow b' = 2 \sqrt{3} \\ Δ' = {(2 \sqrt{3})}^{2} - 1.12 = 0 \end{array}$

Nên phương trình có nghiệm kép

x = - 2 \sqrt{3}

Câu 8:

Giải phương trình sau bằng công thức nghiệm thu gọn:

$25 x^{2} - 10 x + 1 = 0$

Xem đáp án

$\begin{array}{l} 25 x^{2} - 10 x + 1 = 0 \\ a = 25, b = - 10, c = 1 \Rightarrow b' = - 5 \\ Δ' = {(- 5)}^{2} - 25.1 = 0 \end{array}$

Nên phương trình có nghiêm kép :

x = \frac{5}{25} = \frac{1}{5}

Câu 9:

Giải phương trình sau bằng công thức nghiệm thu gọn:

$13 x^{2} - 10 x + 5 = 0$

Xem đáp án

$\begin{array}{l} 13 x^{2} - 10 x + 5 = 0 \\ a = 13, b = - 10, c = 5 \Rightarrow b' = - 5 \\ Δ' = {(- 5)}^{2} - 13.5 = - 40 < 0 \end{array}$

Nên phương trình vô nghiệm

Câu 10:

Giải phương trình sau bằng công thức nghiệm thu gọn:

x^{2} - 6 x + 8 = 0

Xem đáp án

$\begin{array}{l} x^{2} - 6 x + 8 = 0 \\ a = 1, b = - 6, c = 8 \Rightarrow b' = - 3 \\ Δ' = {(- 3)}^{2} - 1.8 = 1 > 0 \end{array}$

Nên phương trình có hai nghiệm phân biệt :

[\begin{array}{l} x_{1} = \frac{3 - \sqrt{1}}{1} = 2 \\ x_{2} = \frac{3 + \sqrt{1}}{2} = 4 \end{array}

Câu 11:

Giải phương trình sau bằng công thức nghiệm thu gọn:

$3 x^{2} - 4 x + 2 = 0$

Xem đáp án

$\begin{array}{l} 3 x^{2} - 4 x + 2 = 0 \\ a = 3, b = - 4, c = 2 \Rightarrow b' = - 2 \\ Δ = {(- 2)}^{2} - 3.2 = - 2 < 0 \end{array}$

Nên phương trình vô nghiệm

Câu 12:

Giải phương trình sau bằng công thức nghiệm thu gọn:

x^{2} - 16 x + 64 = 0

Xem đáp án

$\begin{array}{l} x^{2} - 16 x + 64 = 0 \\ a = 1, b = - 16, c = 64 \Rightarrow b' = - 8 \\ Δ' = {(- 8)}^{2} - 1.64 = 0 \end{array}$

Nên phương trình có nghiệm kép

x = \frac{8}{1} = 8

Câu 13:

Giải phương trình sau bằng công thức nghiệm thu gọn:

5 x^{2} - 6 x - 1 = 0

Xem đáp án

$\begin{array}{l} 5 x^{2} - 6 x - 1 = 0 \\ a = 5, b = - 6, c = 1 \Rightarrow b' = - 3 \\ Δ' = {(- 3)}^{2} - 5. (- 1) = 14 \end{array}$

Nên phương trình có hai nghiệm phân biệt :

[\begin{array}{l} x_{1} = \frac{3 + \sqrt{14}}{2} \\ x_{2} = \frac{3 - \sqrt{14}}{2} \end{array}

Câu 14:

Giải phương trình sau bằng công thức nghiệm thu gọn:

$- 3 x^{2} + 14 x - 8 = 0$

Xem đáp án

$\begin{array}{l} - 3 x^{2} + 14 x - 8 = 0 \\ a = - 3, b = 14, c = - 8 \Rightarrow b' = 7 \\ Δ' = 7^{2} - (- 3) . (- 8) = 25 > 0 \end{array}$

Nên phương trình có hai nghiệm phân biệt :

[\begin{array}{l} x_{1} = \frac{- 7 + \sqrt{25}}{- 3} = \frac{2}{3} \\ x_{2} = \frac{- 7 - \sqrt{25}}{- 3} = 4 \end{array}

Câu 15:

Giải phương trình sau bằng công thức nghiệm thu gọn:

$- 7 x^{2} + 4 x - 3 = 0$

Xem đáp án

$\begin{array}{l} - 7 x^{2} + 4 x - 3 = 0 \\ a = - 7, b = 4, c = - 3 \Rightarrow b' = 2 \\ Δ' = 2^{2} - (- 7) . (- 3) = - 17 < 0 \end{array}$

Nên phương trình vô nghiệm

Câu 16:

Giải phương trình sau bằng công thức nghiệm thu gọn:

$9 x^{2} + 6 x + 1 = 0$

Xem đáp án

$\begin{array}{l} 9 x^{2} + 6 x + 1 = 0 \\ a = 9, b = 6, c = 1 \Rightarrow b' = 3 \\ Δ = 3^{2} - 9.1 = 0 \end{array}$

Nên phương trình có nghiệm kép

x = \frac{- 3}{9} = - \frac{1}{3}

Câu 17:

Giải phương trình sau bằng công thức nghiệm thu gọn:

x^{2} - 12 x + 32 = 0

Xem đáp án

$\begin{array}{l} x^{2} - 12 x + 32 = 0 \\ a = 1, b = - 12, c = 32 \Rightarrow b' = - 6 \\ \Rightarrow Δ' = {(- 6)}^{2} - 1.32 = 4 \end{array}$

Nên phương trình có hai nghiệm phân biệt :

[\begin{array}{l} x_{1} = \frac{6 + \sqrt{4}}{1} = 8 \\ x_{2} = \frac{6 - \sqrt{4}}{1} = 4 \end{array}

Câu 18:

Giải phương trình sau bằng công thức nghiệm thu gọn:

$x^{2} - 6 x - 16 = 0$

Xem đáp án

$\begin{array}{l} x^{2} - 6 x - 16 = 0 \\ a = 1, b = - 6, c = - 16 \Rightarrow b' = - 3 \\ Δ = {(- 3)}^{2} - 1.16 = 25 > 0 \end{array}$

Nên phương trình có hai nghiệm phân biệt :

[\begin{array}{l} x_{1} = 3 + \sqrt{25} = 8 \\ x_{2} = 3 - \sqrt{25} = - 2 \end{array}

Câu 19:

Giải phương trình sau bằng công thức nghiệm thu gọn:

4 x^{2} - 4 x - 7 = 0

Xem đáp án

$\begin{array}{l} 4 x^{2} - 4 x - 7 = 0 \\ a = 4, b = - 4, c = - 7 \Rightarrow b' = - 2 \\ Δ' = {(- 2)}^{2} - 4. (- 7) = 32 \end{array}$

Nên phương trình có hai nghiệm

[\begin{array}{l} x_{1} = \frac{2 + \sqrt{32}}{4} = \frac{1 + 2 \sqrt{2}}{2} \\ x_{2} = \frac{2 - \sqrt{32}}{4} = \frac{1 - 2 \sqrt{2}}{2} \end{array}

Câu 20:

Với giá trị nào của m thì phương trình có hai nghiệm phân biệt :

$x^{2} - 2 (m + 3) x + m^{2} + 3 = 0$

Xem đáp án

$\begin{array}{l} x^{2} - 2 (m + 3) x + m^{2} + 3 = 0 \\ Δ' = {(m + 3)}^{2} - (m^{2} + 3) = 6 m + 6 \end{array}$

Để phương trình có hai nghiệm phân biệt thì : $6 m + 6 > 0 \Leftrightarrow m > - 1$

Câu 21:

Với giá trị nào của m thì phương trình có hai nghiệm phân biệt :

$(m + 1) x^{2} + 4 m x + 4 m - 1 = 0$

Xem đáp án

$\begin{array}{l} (m + 1) x^{2} + 4 m x + 4 m - 1 = 0 (m \neq - 1) \\ Δ' = {(2 m)}^{2} - (m + 1) (4 m - 1) = - 3 m + 1 \end{array}$

Để phương trình có hai nghiệm phân biệt $\Leftrightarrow - 3 m + 1 > 0 \Leftrightarrow m < \frac{1}{3}$

Vậy $m < \frac{1}{3}, m \neq - 1$ thì phương trình có hai nghiệm phân biệt.

Câu 22:

Với giá trị nào của m thì phương trình có nghiệm kép :

$5 x^{2} + 2 m x - 2 m + 15 = 0$

Xem đáp án

$\begin{array}{l} 5 x^{2} + 2 m x - 2 m + 15 = 0 \\ Δ' = m^{2} - 5 (- 2 m + 15) = m^{2} + 10 m - 75 \end{array}$

Để phương trình có nghiệm kép

\Leftrightarrow Δ' = 0 \Leftrightarrow m^{2} + 10 m - 75 = 0 \Leftrightarrow [\begin{array}{l} m = 5 \\ m = - 15 \end{array}

Câu 23:

Với giá trị nào của m thì phương trình có nghiệm kép :

m x^{2} - 4 (m - 1) x - 8 = 0

Xem đáp án

$m x^{2} - 4 (m - 1) x - 8 = 0 (m \neq 0)$

$Δ' = {[- 2 (m - 1)]}^{2} - m . (- 8) = 4 m^{2} + 4 > 0$ (với mọi m)

Nên với mọi m phương trình không có nghiệm kép

Câu 24:

Cho a, b, c là ba số thỏa a > b > c > 0 và a + b + c = 12. Chứng minh rằng trong ba phương trình sau :

$\begin{array}{l} x^{2} + a x + b = 0 (1) \\ x^{2} + b x + c = 0 (2) \\ x^{2} + c x + a = 0 (3) \end{array}$

Có một phương trình có nghiệm, một phương trình vô nghiệm

Xem đáp án

Từ a > b > c > 0 và a + b + c = 12

$\Rightarrow 3 a > a + b + c = 12 > 3 c \Rightarrow a > 4 > c$

$Δ_{1} = a^{2} - 4 b > 4 a - 4 b = 4 (a - b) > 0$ nên phương trình $x^{2} + a x + b = 0$ có nghiệm

$Δ_{2} = c^{2} - 4 a < 4 c - 4 a = 4 (c - a) < 0$ nên phương trình $x^{2} + c x + a = 0$ vô nghiệm.