5 câu hỏi trắc nghiệm thuộc Dạng 1: Góc ở tâm có đáp án

Trắc nghiệm Chuyên đề Toán 9 Chuyên đề 4: Góc và đường tròn có đáp án

Dạng 1: Góc ở tâm có đáp án

774 lượt thi
5 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hình vẽ sau:

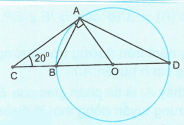
Tính số đo cung nhỏ AB và $\hat{A D B}$ từ đó so sánh hai đoạn thẳng AC và AD.

Xem đáp án

Xét tam giác ACO vuông tại A có

\hat{A C O} = 20 °

nên $\hat{A O C} = 90 ° - 20 ° = 70 ° \Rightarrow s đ \overset{⏜}{A B} = 70 °$ .

$\hat{A O B}$ là góc ngoài của tam giác cân AOD nên $\hat{A D B} = \frac{1}{2} \hat{A O B} = \frac{1}{2} .70 ° = 35 °$ .

Xét $Δ A C D$ có $20 ° = \hat{A C D} < \hat{A D C} = 35 ° \Rightarrow A C > A D$ .

Câu 2:

Cho hình vẽ sau, tính số đo cung nhỏ AB, biết rằng B là trung điểm OC.

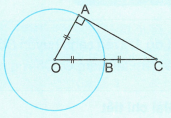
Xem đáp án

Tam giác vuông AOC có AB là trung tuyến ứng với cạnh huyền OC nên $B A = B C = B O$ .

Do đó $Δ A O B$ là tam giác đều $\Rightarrow \hat{A O B} = 60 °$ . Suy ra số đo cung nhỏ AB là 60 độ .

Câu 3:

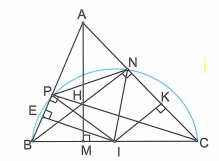
Cho tam giác nhọn ABC có trực tâm H và $\hat{B A C} = 60 °$ . Gọi M,N,P theo thứ tự là chân các đường cao kẻ từ các đỉnh A,B,C của tam giác ABC và I là trung điểm của BC.

a) Chứng minh rằng tam giác INP đều.

Xem đáp án

a) Ta thấy $Δ B N C$ và $Δ B P C$ là hai tam giác vuông có chung cạnh huyền BC nên bốn điểm B,P,N,C nằm trên đường tròn tâm I, đường kính BC.

Khi đó $I N = I P \Rightarrow Δ I N P$ cân tại I. (1)

Tam giác ABN vuông tại N có: $\hat{A B N} + \hat{B A N} = 90 ° \Rightarrow \hat{A B N} = 90 ° - \hat{B A N} = 30 °$ .

Ta có $\hat{P B N}$ là góc nội tiếp và $\hat{P I N}$ là góc ở tâm cùng chắn cung $\overset{⏜}{N P}$ .

Do đó $\hat{P I N} = 2 \hat{P B N} = 60 °$ . (2)

Từ (1) và (2) suy ra $Δ I N P$ đều.

Câu 4:

b) Gọi E và K lần lượt là trung điểm của PB và NC. Chứng minh rằng các điểm I,M,E,K cùng thuộc một đường tròn.

Xem đáp án

b) $I P = I B$ (bán kính đường tròn $(I)$ )

$\Rightarrow Δ I B P$ cân $\Rightarrow I E ⊥ B P$ .

Tương tự có $I K ⊥ N C$ .

Do đó, bốn điểm $I, M, E, K$ cùng nằm trên đường tròn đường kính $A I$ (vì các tam giác vuông $A E I, A M I$ và AKI có chung cạnh huyền AI).

Câu 5:

c) Giả sử IA là phân giác của $\hat{N I P}$ . Tìm số đo $\hat{B C P}$ .

Xem đáp án

c) Từ điều kiện của bài toán ta thấy AI là tia phân giác của $\hat{B A C}$ mà AI là trung tuyến của $Δ A B C$ nên $Δ A B C$ cân tại A (do trung tuyến đồng thời là đường phân giác).

Mặt khác, $\hat{B A C} = 60 °$ nên $Δ A B C$ đều.

Trong tam giác vuông BPC có $\hat{P B C} = 60 ° \Rightarrow \hat{B C P} = 90 ° - \hat{P B C} = 30 °$ .

Vậy $\hat{B C P} = 30 °$ .

Bắt đầu thi ngay