15 câu trắc nghiệm Toán 9 Cánh diều Ôn tập chương VIII có đáp án
-
46 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Phương án A, B, C đúng.
Phương án D sai. Sửa lại: Đường tròn ngoại tiếp một tam giác là đường tròn đi qua cả ba đỉnh của tam giác đó.
Vậy ta chọn phương án D.
Câu 2:
Đường tròn ngoại tiếp đa giác là đường tròn
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Đường tròn ngoại tiếp đa giác là đường tròn đi qua tất cả các đỉnh của đa giác đó.
Câu 3:
Trong các hình sau, hình nội tiếp được trong đường tròn là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hình thoi và hình vuông có đường chéo cắt nhau tại trung điểm mỗi đường nên nội tiếp đường tròn có tâm là giao điểm hai đường chéo và bán kính bằng nửa đường chéo.
Câu 4:
Cho các hình vẽ sau:
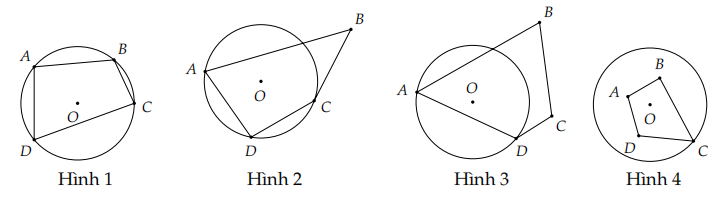
Trong các hình trên, hình nào đang nội tiếp đường tròn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta thấy trên hình 1, các điểm \[A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\] đều nằm trên đường tròn \[\left( O \right)\] nên tứ giác \[ABCD\] trên hình 1 là tứ giác nội tiếp.
Câu 5:
Tứ giác nội tiếp đường tròn là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên đường tròn đó.
Vậy ta chọn phương án A.
Câu 6:
II. Thông hiểu
Khi tứ giác \[MNPQ\] nội tiếp đường tròn, và có \(\widehat M = 90^\circ \). Khi đó, góc \[P\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
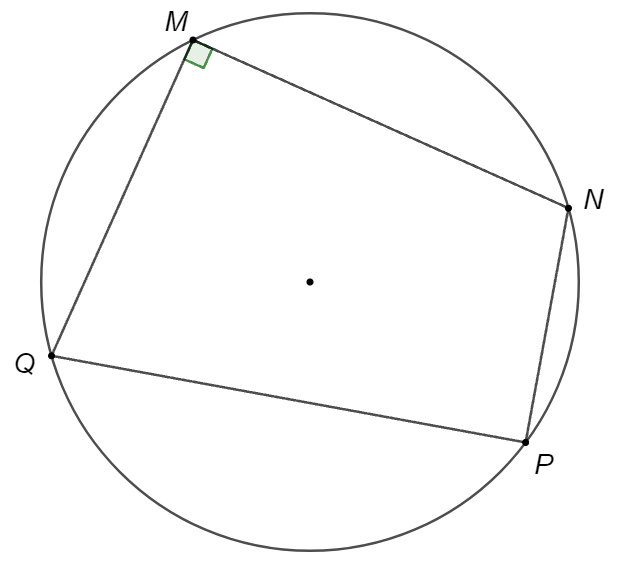
Tứ giác \[MNPQ\] nội tiếp đường tròn nên \(\widehat M + \widehat P = 180^\circ \) hay \(\widehat P = 180^\circ - \widehat M = 180^\circ - 90^\circ = 90^\circ \).
Câu 7:
Tam giác đều \[ABC\] nội tiếp đường tròn. Khi đó góc \[AOB\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
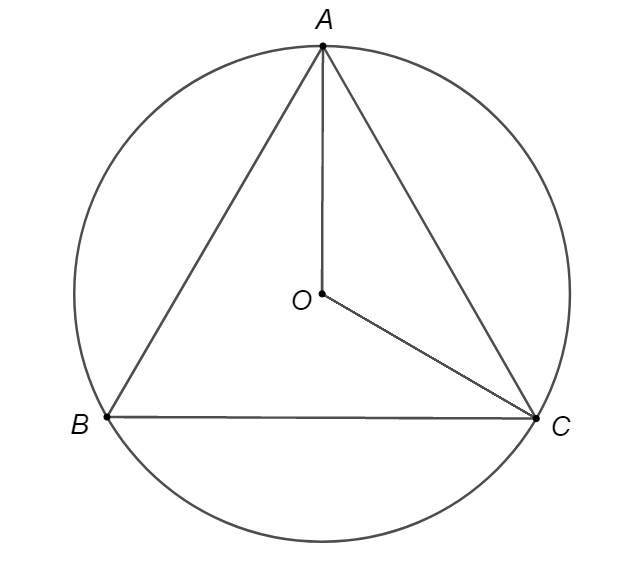
Góc \[AOB\] và \[ACB\] lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung \[AB\] của đường tròn \[\left( O \right)\] nên \(\widehat {AOB} = 2\widehat {ACB} = 2 \cdot 60^\circ = 120^\circ \).
Câu 8:
Cho tam giác \[MNP\] đều cạnh bằng \[\sqrt 3 \] dm. Khi đó bán kính \[R\] của đường tròn ngoại tiếp và bán kính \[r\] của đường tròn nội tiếp tam giác đều \[MNP\] lần lượt bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Bán kính R của đường tròn ngoại tiếp tam giác đều \[MNP\] là:
\[R = \frac{{a\sqrt 3 }}{3} = \frac{{\sqrt 3 \cdot \sqrt 3 }}{3} = 1\] (dm).
Bán kính r của đường tròn nội tiếp tam giác đều \[MNP\] là:
\[r = \frac{{a\sqrt 3 }}{6} = \frac{{\sqrt 3 \cdot \sqrt 3 }}{6} = \frac{1}{2} = 0,5\] (dm).
Do đó ta chọn phương án D.
Câu 9:
Cho tứ giác \[ABCD\] nội tiếp một đường tròn \[\left( O \right)\]. Biết \(\widehat {BOD} = 140^\circ \). Số đo góc \(\widehat {BCD}\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
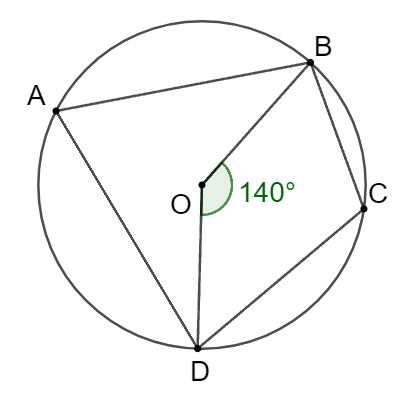
Góc \[BAD\] và \[BOD\] là góc nội tiếp và góc ở tâm cùng chắn cung \[BD\] của \[\left( O \right)\].
Do đó \(\widehat {BAD} = \frac{1}{2}\widehat {BOD} = \frac{1}{2}.140^\circ = 70^\circ \).
Tứ giác \[ABCD\] là tứ giác nội tiếp nên \(\widehat {BAD} + \widehat {BCD} = 180^\circ \).
Vậy \(\widehat {BCD} = 180^\circ - \widehat {BAD} = 180^\circ - 70^\circ = 110^\circ \).
Câu 10:
Cho hình vẽ bên dưới.
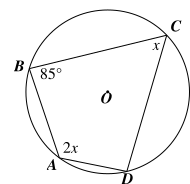
Giá trị của \[x\] và số đo \[\widehat {ADC}\] lần lượt bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tứ giác \[ABCD\] nội tiếp đường tròn \[\left( O \right)\] có: \[\widehat {BAD} + \widehat {BCD} = 180^\circ \] (tổng hai góc đối của tứ giác nội tiếp).
Suy ra \[2x + x = 180^\circ \]
\[3x = 180^\circ \]
\[x = 60^\circ .\]
Tứ giác \[ABCD\] nội tiếp đường tròn \[\left( O \right)\] có: \[\widehat {ADC} + \widehat {ABC} = 180^\circ \] (tổng hai góc đối của tứ giác nội tiếp).
Suy ra \[\widehat {ADC} = 180^\circ - \widehat {ABC} = 180^\circ - 85^\circ = 95^\circ .\]
Vậy \[x = 60^\circ \] và \[\widehat {ADC} = 95^\circ .\]
Câu 11:
Cho tứ giác \[ABCD\] nội tiếp đường tròn \[\left( {O;{\rm{ }}R} \right).\] Biết rằng \[\widehat {ABC} = 70^\circ ;\,\,\widehat {ODC} = 50^\circ .\] Số đo \[\widehat {AOD}\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
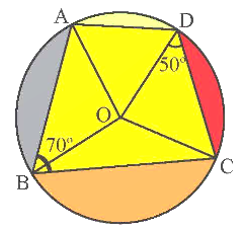
Tứ giác \[ABCD\] nội tiếp đường tròn \[\left( {O;{\rm{ }}R} \right)\] có: \[\widehat {ADC} + \widehat {ABC} = 180^\circ \] (tổng hai góc đối của tứ giác nội tiếp).
Suy ra \[\widehat {ADC} = 180^\circ - \widehat {ABC} = 180^\circ - 70^\circ = 110^\circ .\]
Ta có \[\widehat {ADO} + \widehat {ODC} = \widehat {ADC}\,.\]
Suy ra \[\widehat {ADO} = \widehat {ADC} - \widehat {ODC} = 110^\circ - 50^\circ = 60^\circ .\]
Tam giác \[OAD\] cân tại \[O\] (do \[OA = OD = R\]) có \[\widehat {ADO} = 60^\circ \] nên \[\Delta OAD\] là tam giác đều. Do đó \[\widehat {AOD}\, = 60^\circ .\]
Câu 12:
Tứ giác \[ABCD\] nội tiếp đường tròn có hai cạnh đối \[AB\] và \[CD\] cắt nhau tại \[M\] và \(\widehat {BAD} = 70^\circ \). Số đo \(\widehat {BCM}\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
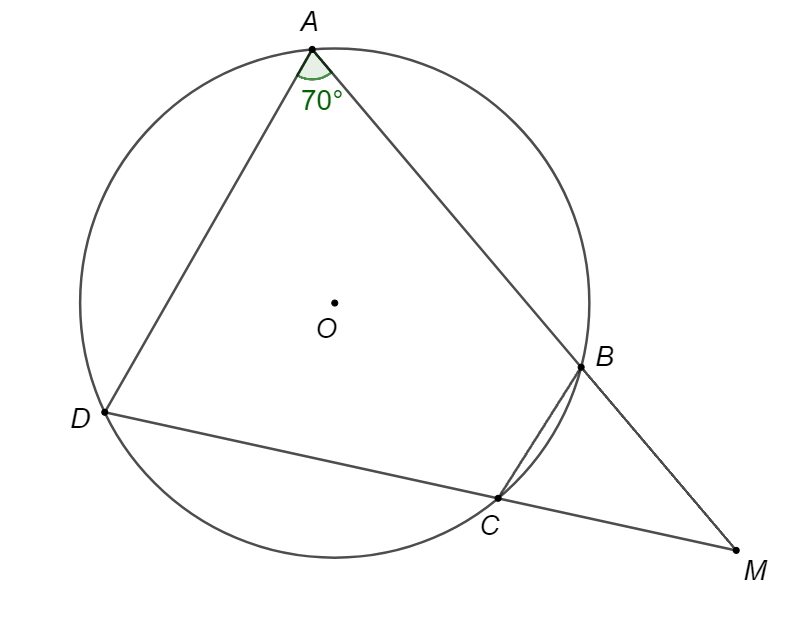
Tứ giác \[ABCD\] nội tiếp nên ta có:
\(\widehat {DAB} + \widehat {BCD} = 180^\circ \) nên \(\widehat {BCD} = 180^\circ - 70^\circ = 110^\circ \).
Mà \(\widehat {BCD} + \widehat {BCM} = 180^\circ \) (hai góc kề bù)
Do đó \(\widehat {BCM} = 180^\circ - 110^\circ = 70^\circ \).
Vậy \(\widehat {BCM} = 70^\circ \).
Câu 13:
III. Vận dụng
Người ta làm một khung gỗ hình tam giác đều đặt vừa khít một chiếc đồng hồ hình tròn có đường kính \[40{\rm{ cm}}.\]
![Người ta làm một khung gỗ hình tam giác đều đặt vừa khít một chiếc đồng hồ hình tròn có đường kính \[40{\rm{ cm}}.\] Độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu (làm tr (ảnh 1)](https://video.vietjack.com/upload2/images/1731559220/1731559937-image8.png)
Độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Bán kính của chiếc đồng hồ hình tròn là: \[r = \frac{{40}}{2} = 20\,\,\left( {{\rm{cm}}} \right).\]
Gọi \[a{\rm{ }}\left( {{\rm{cm}}} \right)\] là độ dài cạnh (phía bên trong) của khung gỗ.
Ta có \[r = \frac{{a\sqrt 3 }}{6},\] hay \[\frac{{a\sqrt 3 }}{6} = 20,\] suy ra \[a = 40\sqrt 3 \approx 69,28\,\,\left( {{\rm{cm}}} \right).\]
Vậy độ dài các cạnh (phía bên trong) của khung gỗ khoảng bằng \[69,28\,\,{\rm{cm}}.\]
Câu 14:
Cho tứ giác \[ABCD\] nội tiếp đường tròn \[\left( O \right)\] sao cho tam giác \[ABC\] nhọn. Hai đường cao \[AM,{\rm{ }}CN\] của tam giác \[ABC\] cắt nhau tại \[H.\] Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
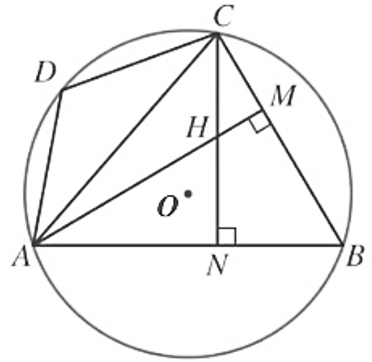
Xét phương án A:
a) Ta có \[\widehat {HMB} = \widehat {HNB} = 90^\circ \] (do \[AM,{\rm{ }}CN\] là hai đường cao cắt nhau tại \[H\] của tam giác ABC).
Do đó hai điểm \[M,{\rm{ }}N\] cùng nằm trên đường tròn đường kính \[HB.\]
Khi đó tứ giác \[HMBN\] nội tiếp đường tròn đường kính \[HB.\]
Vậy \[\widehat {MHN} + \widehat {MBN} = 180^\circ \] hay \[\widehat {MHN} + \widehat {ABC} = 180^\circ .\]
Xét phương án B:
Ta có tứ giác \[ABCD\] nội tiếp đường tròn \[\left( O \right)\] nên \[\widehat {ADC} + \widehat {ABC} = 180^\circ .\]
Mà \[\widehat {MHN} + \widehat {ABC} = 180^\circ \] (câu a) nên \[\widehat {ADC} = \widehat {MHN}\,.\]
Lại có \[\widehat {AHC} = \widehat {MHN}\] (cặp góc đối đỉnh) nên \[\widehat {AHC} = \widehat {ADC}\,.\]
Xét phương án C:
Tam giác ABM, có: \[\widehat {AMB} + \widehat {BAM} + \widehat {ABC} = 180^\circ \] (tổng ba góc của một tam giác)
Mà \[\widehat {ADC} + \widehat {ABC} = 180^\circ \] (chứng minh trên)
Suy ra \[\widehat {ADC} = \widehat {AMB} + \widehat {BAM} = 90^\circ + \widehat {BAM}\,.\]
Vậy \[\widehat {ADC} = \widehat {BAM} + 90^\circ .\]
Do đó chọn phương án D.
Câu 15:
Người ta cần xây dựng một khung cổng hình chữ nhật rộng 4 m và cao 3 m, bên ngoài khung cổng được bao bởi một khung thép dạng nửa hình tròn (như hình vẽ).
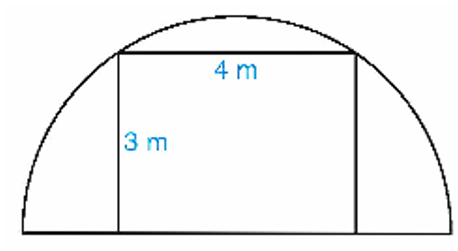
Chiều dài của đoạn thép dùng để làm khung nửa đường tròn đó là bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
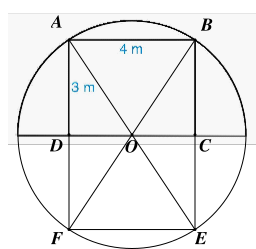
Gọi \[ABCD\] là khung cổng hình chữ nhật.
Vẽ hình chữ nhật \[ABEF\] (hình vẽ) và \[O\] là giao điểm của hai đường chéo \[AE,{\rm{ }}BF.\]
Khi đó ta có \[AF = 2AD = 2 \cdot 3 = 6{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\]
Tam giác \[ABF\] vuông tại A, theo định lí Pythagore, ta có:
\[B{F^2} = A{F^2} + A{B^2} = {6^2} + {4^2} = 52.\]
Do đó \[BF = \sqrt {52} = 2\sqrt {13} \,\,\left( {{\rm{cm}}} \right).\]
Vì vậy bán kính đường tròn ngoại tiếp hình chữ nhật \[ABEF\] là: \[R = \frac{{BF}}{2} = \sqrt {13} \,\,\left( {{\rm{cm}}} \right).\]
Chu vi đường tròn ngoại tiếp hình chữ nhật \[ABEF\] là: \[C = 2\pi R = 2\pi \sqrt {13} \,\,\left( {{\rm{cm}}} \right).\]
Vậy chiều dài của đoạn thép dùng để làm khung nửa đường tròn là \[\frac{C}{2} = \frac{{2\pi \sqrt {13} }}{2} \approx 11,33\,\,\left( {{\rm{cm}}} \right).\]
