17 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 23

Câu 1:

Cho AB, AC là hai dây cung trong đường tròn (O). Gọi M là trung điểm của cung AB và N là trung điểm của cung AC. Đường thẳng MN cắt dây AB tại D và cắt dây AC tại E. Chứng minh AD = AE.

Xem đáp án

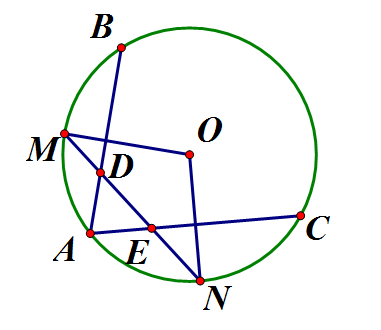
Cho AB, AC là hai dây cung trong đường tròn (O). Gọi M là trung điểm (ảnh 1)

$\overset{⏜}{A M} = \overset{⏜}{M B} (g t), \overset{⏜}{A N} = \overset{⏜}{N C} (g t)$
$\Rightarrow ∠ A D E = \frac{s d \overset{⏜}{A N} + s d \overset{⏜}{M B}}{2}$ (góc có đỉnh bên trong đường tròn)

$∠ A E D = \frac{s d \overset{⏜}{N C} + s d \overset{⏜}{A M}}{2}$ (góc có đỉnh bên trong đường tròn)

$\Rightarrow ∠ A D E = ∠ A E D \Rightarrow Δ A D E$ cân tại A $\Rightarrow A D = A E$

Câu 2:

Cho đường tròn (O), các điểm A, B, C, D theo thứ tự đó ở trên đường tròn. Điểm M ở trên cung AB và MA = MB. Giao điểm của MC, MD với dây AB là E, K.

Chứng minh $∠ K E C + ∠ K D C = 180^{0}$

Xem đáp án

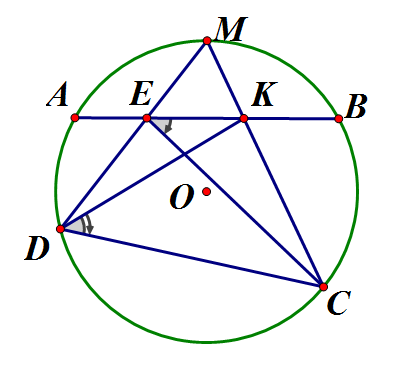
Cho đường tròn (O), các điểm A, B, C, D theo thứ tự đó ở trên đường tròn. Điểm (ảnh 1)

A M = M B (g t) \Rightarrow \overset{⏜}{A M} = \overset{⏜}{M B}

∠ K E C = \frac{s d \overset{⏜}{M B} + s d \overset{⏜}{A C}}{2}

(góc có đỉnh bên trong đường tròn)

$∠ K D C = \frac{s d \overset{⏜}{M C}}{2}$ (góc nội tiếp). Do đó:

$∠ K E C + ∠ K D C = \frac{s d \overset{⏜}{M B} + s d \overset{⏜}{A C} + s d \overset{⏜}{M C}}{2} = \frac{s d \overset{⏜}{M A} + s d \overset{⏜}{A C} + s d \overset{⏜}{M C}}{2} = \frac{360^{0}}{2} = 180^{0}$

Câu 3:

Trên đường tròn (O) lấy ba điểm A, B, C. Gọi M, N, P theo thứ tự là các điểm chính giữa của các cung AB, BC, AC. Gọi I là giao điểm của AB và MN, K là giao điểm của AN, BP. Chứng minh rằng:

$a) Δ B N K$ cân $b) I K / / B C c) A I . B N = I B . A N$

Xem đáp án

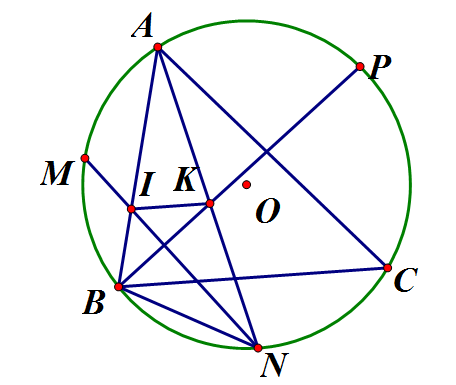
Trên đường tròn (O) lấy ba điểm A, B, C. Gọi M, N, P theo thứ tự là các điểm (ảnh 1)

Ta có: $∠ P B N = \frac{1}{2} (s d \overset{⏜}{P C} + s d \overset{⏜}{C N})$ (góc nội tiếp cùng chắn $\overset{⏜}{P N})$

$∠ B C N = \frac{1}{2} (s d \overset{⏜}{A P} + s d \overset{⏜}{B N})$ (góc có đỉnh bên trong đường tròn)

Mà PC = AP và $C N = B N (g t) \Rightarrow ∠ P B N = ∠ B C N$

Dễ thấy $∠ A N M = ∠ B N M$ (góc nội tiếp chắn hai cung bằng nhau) nên NI là phân giác $∠ A N B$

Ta có: $\frac{A I}{I B} = \frac{A N}{B N} \Rightarrow A I . B N = I B . A N$

Theo chứng minh trên (câu a, b) , $Δ B N K$ cân có NI là đường phân giác . Do đó IN cũng là đường trung trực của cạnh $B K \Rightarrow I B = I K \Rightarrow Δ B I K$ cân $\Rightarrow ∠ I B K = ∠ I K B$ hay $∠ A B D = ∠ I K B (1)$ mà $∠ A P B = ∠ C B P (2)$ (góc nội tiếp chắn 2 cung bằng nhau)

Từ (1) và (2) suy ra $∠ C B D = ∠ I K P \Rightarrow I K / / B C$

Câu 4:

Cho tam giác ABC. Giả sử các đường phân giác trong và phân giác ngoài của $∠ A$ của tam giác ABC lần lượt cắt BC tại D, E có AD = AE

Chứng minh $A B^{2} + A C^{2} = 4 R^{2}$ với R là bán kính đường tròn ngoại tiếp $Δ A B C$

Xem đáp án

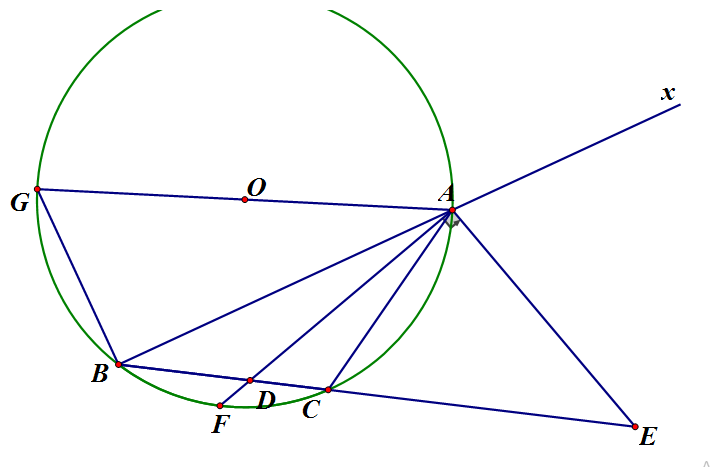
Cho tam giác ABC. Giả sử các đường phân giác trong và phân giác ngoài của (ảnh 1)

AD cắt cung BC tại F. Vẽ đường kính AC của đường tròn (ABC)

Ta có: $∠ A B G = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)

$s d \overset{⏜}{G B} + s d \overset{⏜}{F C} + s d \overset{⏜}{A C} + s d \overset{⏜}{B F} = s d \overset{⏜}{A C G} = 180^{0}$

$∠ B A F = ∠ F A C$ (AD là phân giác) $\Rightarrow s d \overset{⏜}{B F} = s d \overset{⏜}{F C}$

Nên AD, AE là hai tia phân giác của hai góc kề bù $∠ B A C, ∠ C A x$ nên $∠ D A E = 90^{0} (1)$
$Δ D A E$ vuông góc có $A D = A E (g t) \Rightarrow Δ D A E$ vuông cân $\Rightarrow ∠ A D E = 45^{0} (2)$

sđ $\overset{⏜}{A D E} = \frac{s d \overset{⏜}{A C} + s d \overset{⏜}{B F}}{2} \Rightarrow s d \overset{⏜}{A C} + s d \overset{⏜}{B F} = 90^{0} (3)$

Từ (1), (2), (3) có $\overset{⏜}{G B} = \overset{⏜}{A C} \Rightarrow G B = A C$

$Δ B A G$ vuông tại B nên $A B^{2} + B G^{2} = A G^{2} = A B^{2} + A C^{2} = 4 R^{2}$

Câu 5:

Một ca nô dự định đi từ A đến B trong thời gian dự định. Nếu ca nô tăng 3km/h thì đến nơi sớm 2 giờ. Nếu ca nô giảm vận tốc 3km/hthì đến nơi chậm 3 giờ. Tính chiều dài khúc sông AB.

Xem đáp án

Gọi x là vận tốc dự định ban đầu (km/h) (x > 3)

y là thời gian dự định ban đầu (y > 0), độ dài khúc sông là xy (km)

Nếu ca nô tăng 3km/h thì đến nơi sớm 2h nên ta có phương trình: $(x + 3) (y - 2) = x y (1)$

Nếu cano giảm vận tốc 3km/h thì đến nơi chậm $3 h \Rightarrow (x - 3) (y + 3) = x y (2)$

Từ (1), (2) ta có hệ $\{\begin{cases} (x + 3) (y - 2) = x y \\ (x - 3) (y + 3) = x y \end{cases} \Leftrightarrow \{\begin{cases} - 2 x + 3 y = 6 \\ 3 x - 3 y = 9 \end{cases} \Leftrightarrow \{\begin{cases} x = 12 \\ y = 15 \end{cases}$

Vậy khúc sông $A B = 12.15 = 180 (k m)$

Câu 6:

Một hình chữ nhật có chu vi 110m. Hai lần chiều dài hơn ba lần chiều rộng là 10m. Tính diện tích hình chữ nhật

Xem đáp án

Gọi chiều dài hình chữ nhật là a (m) (a > 0), chiều rộng hình chữ nhật b (m) (b > 0)

Ta có: $a + b = \frac{110}{2} = 55 (1)$

Ta lại có 2 lần chiều dài hơn 3 lần chiều rộng là $10 m \Rightarrow 2 a - 3 b = 10 (2)$

Từ (1) và (2) suy ra $\{\begin{cases} a + b = 55 \\ 2 a - 3 b = 10 \end{cases} \Leftrightarrow \{\begin{cases} a = 35 \\ b = 20 \end{cases} (t m)$

Vậy diện tích hình chữ nhật : $35.20 = 700 (m^{2})$

Câu 7:

Một người đi xe đạp dự định đi hết quãng đường AB với vận tốc 10 km/h. Sau khi đi được nửa quãng đường với vận tốc dự định người ấy nghỉ 30 phút. Vì muốn đến được điểm B kịp giờ nên người đó đi với vận tốc 15 km/h trên quãng đường còn lại. Tính quãng đường AB.

Xem đáp án

Thời gian đi nửa quãng đường đầu là : $\frac{A B}{2} : 10 = \frac{A B}{20}$ (giờ)

Thời gian đi nửa quãng đường sau là : $\frac{A B}{2} : 15 = \frac{A B}{30}$ (giờ)

$\Rightarrow \frac{A B}{20} - \frac{A B}{30} = 0, 5 \Leftrightarrow A B = 30 (k m)$ . Vậy AB = 30 km.

Câu 8:

Hai người cùng làm một công việc trong 7 giờ 12 phút thì xong công việc. Nếu người thứ nhất làm trong 4 giờ, người thứ hai làm trong 3 giờ thì được 50% công việc. Hỏi mỗi người làm một mình trong mấy giờ thì xong công việc ?

Xem đáp án

Gọi thời gian người thư nhất và người thứ hai làm một mình xong công việc lần lượt là x, y (giờ), (x, y > 7)

Mỗi giờ người thứ nhất và người thứ hai làm được $\frac{1}{x}, \frac{1}{y} (C V)$ , nên ta có hệ phương trình:

$\{\begin{cases} \frac{1}{x} + \frac{1}{y} = \frac{5}{36} \\ \frac{4}{x} + \frac{3}{y} = 50 % \end{cases} \Leftrightarrow \{\begin{cases} x = 12 \\ y = 18 \end{cases} (t m)$

Vậy người thứ nhất 12 giờ làm xong, người thứ hai 18 giờ làm xong.

Câu 9:

Một đoàn xe vận tải có 15 xe tải lớn và 4 xe tải nhỏ tất cả chở 178 tấn hàng. Biết mỗi xe tải lớn chở nhiều hơn xe tải nhỏ là 3 tấn. Tính số tấn hàng mỗi xe tải từng loại đã chở.

Xem đáp án

Giả sử xe tải lớn chở a (tấn), xe tải nhỏ chở b (tấn)

Theo đề ta có hệ phương trình $\{\begin{cases} 15 a + 4 b = 178 \\ a - b = 3 \end{cases} \Leftrightarrow \{\begin{cases} a = 10 \\ b = 7 \end{cases} (t m)$

Vậy xe tải lớn: 10 tấn, xe tải nhỏ: 30 tấn.

Câu 10:

Một ô tô đi từ A đến B với vận tốc và thời gian quy định. Nếu vận tốc ô tô tăng thêm 10 km/h thì đến B sớm hơn 30 phút so với dự đinh. Nếu vận tốc ô tô giảm đi 5 km/h thì đến B muộn hơn 20 phút so với dự định. Tìm quãng đường AB.

Xem đáp án

Gọi vận tốc dự định là x (x > 0), thời gian dự định là t (t > 0). Ta có:

Nếu tăng vận tốc lên 10 km/h thì sớm hơn $\frac{1}{2}$ giờ nên $x t = (x + 10) (t - \frac{1}{2}) (1)$

Nếu giảm đi 5 km/hthì muộn hơn $\frac{1}{3}$ giờ nên $x t = (x - 5) (t + \frac{1}{3}) (2)$

Từ (1) và (2) ta có hệ

\{\begin{cases} - \frac{1}{2} x + 10 t = 5 \\ \frac{1}{3} x - 5 t = \frac{5}{3} \end{cases} \Leftrightarrow \{\begin{cases} x = 50 \\ t = 3 \end{cases} (t m) \Rightarrow A B = 50.3 = 150 (k m)

Câu 11:

Một mảnh đất hình chữ nhật có chu vi là 90m. Nếu giảm chiều dài 5m và chiều rộng 2m thì diện tích giảm $140 m^{2} .$ Tính diện tích mảnh đất đó.

Xem đáp án

Gọi chiều dài mảnh đất là x (m), chiều rộng mảnh đất là y (m) (x, y > 0)

Theo bài ta có: $\{\begin{cases} 2 (x + y) = 90 \\ (x - 5) (y - 2) = x y - 140 \end{cases} \Leftrightarrow \{\begin{cases} x + y = 45 \\ 2 x + 5 y = 150 \end{cases} \Leftrightarrow \{\begin{cases} x = 25 \\ y = 20 \end{cases} (t m)$

Diện tích mảnh đất: $25.20 = 500 (m^{2})$

Câu 12:

Có hai ô tô khởi hành cùng một lúc từ 2 tỉnh A và B cách nhau 105km. Nếu đi ngược chiều hai xe gặp nhau sau 5 giờ. Tìm vận tốc mỗi xe, biết rằng xe đi từ A nhanh hơn xe kia 10km mỗi giờ.

Xem đáp án

Gọi x, y lần lượt là vận tốc 2 xe (x > 0, y > 0), tổng vận tốc 2 xe: $\frac{105}{5} = 21$

Ta có hệ phương trình: $\{\begin{cases} x + y = 21 \\ x - y = 10 \end{cases} \Leftrightarrow \{\begin{cases} x = 15, 5 \\ y = 5, 5 \end{cases} (t m)$

Vậy vận tốc xe A: 15,5(km/h) vận tốc xe B: 5,5 (km/h)

Câu 13:

Trong một trang sách, nếu bớt đi 5 dòng và mỗi dòng bớt đi 2 chữ thì cả trang sách sẽ bớt đi 150 chữ. Nếu tăng thêm 6 dòng và mỗi dòng thêm 3 chữ thì cả trang sách sẽ tăng thêm 228 chữ. Tính số dòng trong trach sách và số chữ mỗi dòng, biết số chữ của mỗi dòng đều bằng nhau.

Xem đáp án

Gọi x là số dòng, y là số chữ mỗi dòng (x, y > 0)

Theo đề bớt 5 dòng , mỗi dòng bớt 2 chữ thì bớt 150 chữ

$\Rightarrow (x - 5) (y - 2) = x y - 150 \Rightarrow - 2 x - 5 y = - 160 (1)$

Tăng 6 chữ, mỗi dòng thêm 3 chữ thì thêm 228 chữ

$\Rightarrow (x + 6) (y + 3) = x y + 228 \Rightarrow 3 x + 6 y = 210 (2)$

Từ (1) và (2) ta có hệ: $\{\begin{cases} - 2 x - 5 y = - 160 \\ 3 x + 6 y = 210 \end{cases} \Leftrightarrow \{\begin{cases} x = 30 \\ y = 20 \end{cases} (t m)$

Vậy có 30 dòng, 20 chữ.

Câu 14:

Một ô tô và một mô tô khởi hành cùng một lúc từ 2 địa điểm A, B cách nhau 200km đi ngược chiều và gặp nhau sau 2,5 giờ. Tính vận tốc của ô tô và mô tô, biết rằng vận tốc mô tô nhỏ hơn vận tốc ô tô là 20 km/h.

Xem đáp án

Gọi x (km/h) là vận tốc mô tô, y (km/h) là vận tốc ô tô (y > x > 0)

Tổng vận tốc $= \frac{200}{2, 5} = 80 \Rightarrow x + y = 80$

Theo bài ta có hệ $\{\begin{cases} y + x = 80 \\ y - x = 20 \end{cases} \Leftrightarrow \{\begin{cases} x = 30 \\ y = 50 \end{cases} (t m)$

Vậy vận tốc ô tô: 50 km/h, vận tốc mô tô: 30km/h

Câu 15:

Một ô tô đi trên đoạn đường AB với vận tốc 55 km/h, rồi tiếp tục từ B đến C với vận tốc tăng thêm 5km/h. Biết quãng đường tổng cộng dài 290km và thời gian ô tô đi trên đoạn đường AB ít hơn thời gian ô tô đi trên đoạn đường BC là 1 giờ. Tính thời gian ô tô đi trên mỗi đoạn đường AB và BC.

Xem đáp án

Gọi thời gian đi trên AB là t (t > 0), thời gian đi trên BC là $t + 1 \Rightarrow A B = t . v = 55 t$

$B C = (t + 1) (v + 5) = 60 t + 60$

$S_{B C} = 290 \Leftrightarrow 55 t + 60 t + 60 = 290 \Leftrightarrow t = 2$

Vậy ô tô đi trên AB hết 2h , đi trên BC hết 3 giờ

Câu 16:

Tìm hai số biết tổng của chúng bằng 7 và tổng nghịch đảo bằng $\frac{7}{12}$

Xem đáp án

Gọi 2 số đó là x, y theo bài ta có hệ

$\{\begin{cases} x + y = 7 \\ \frac{1}{x} + \frac{1}{y} = \frac{7}{12} \end{cases} \Leftrightarrow \{\begin{cases} x + y = 7 \\ x + y = \frac{7}{12} x y \end{cases} \Leftrightarrow [\begin{array}{l} \{\begin{cases} x = 4 \\ y = 4 \end{cases} \\ \{\begin{cases} x = 3 \\ y = 4 \end{cases} \end{array}$ . Vậy 2 số cần tìm là 3; 4.

Câu 17:

Một ca nô xuôi dòng 108km, rồi ngược dòng 63km mất 7 giờ. Lần thứ hai, ca nô đó xuôi dòng 81km rồi ngược dòng 84km cũng mất 7 giờ. Tính vận tốc dòng nước và vận tốc thực của ca nô.

Xem đáp án

Gọi vận tốc cano là x (km/h), vận tốc dòng nước là y (km/h) (x > y > 0)

Thời gian xuôi dòng $108 k m : \frac{108}{x + y} (h)$

Thời gian ngược dòng $63 k m : \frac{63}{x - y} \Rightarrow \frac{108}{x + y} + \frac{63}{x - y} = 7 (1)$

Chứng minh tương tự $\Rightarrow \frac{81}{x + y} + \frac{84}{x - y} = 7 (2)$

Từ (1) và (2) ta có hệ:

$\{\begin{cases} \frac{108}{x + y} + \frac{63}{x - y} = 7 \\ \frac{81}{x + y} + \frac{84}{x - y} = 7 \end{cases} \Leftrightarrow \{\begin{cases} x = 24 \\ y = 3 \end{cases} (t m)$

Vậy vận tốc nước: 3 km/h, vận tốc ca nô : 24 km/h.