Trắc nghiệm Toán 9 Cánh diều Bài 2. Một số hệ thức về cạnh và góc trong tam giác vuông có đáp án
Trắc nghiệm Toán 9 Cánh diều Bài 2. Một số hệ thức về cạnh và góc trong tam giác vuông có đáp án
-
52 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Cho hình vẽ dưới đây.
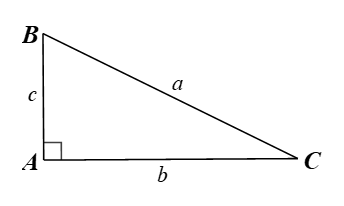
Hệ thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì tam giác \[ABC\] vuông tại \[A\] nên:
⦁ \[c = a.\cos B = a.\sin C\,;\]
⦁ \[c = b.\cot B = b.\tan C.\]
Vậy ta chọn phương án D.
Câu 2:
Cho hình vẽ dưới đây.
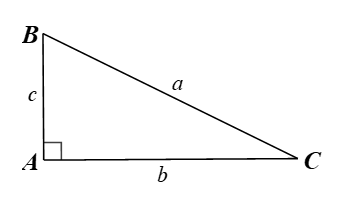
Hệ thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì tam giác \[ABC\] vuông tại \[A\] nên:
⦁ \[b = c\tan B = c\cot C\,;\]
⦁ \[c = b\tan C = b\cot B.\]
Vậy ta chọn phương án A.
Câu 3:
Bài toán “giải tam giác vuông” là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Trong một tam giác vuông, nếu cho biết độ dài hai cạnh hoặc độ dài một cạnh và số đo một góc nhọn thì ta sẽ tìm được tất cả độ dài các cạnh và số đo các góc còn lại của tam giác đó. Bài toán đặt ra như thế gọi là bài toán “giải tam giác vuông”.
Vậy ta chọn phương án A.
Câu 4:
Nếu tam giác \[MNP\] vuông tại \[M\] có \[NP = 5,\,\,\cos N = \frac{3}{5}\] thì \[MN\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
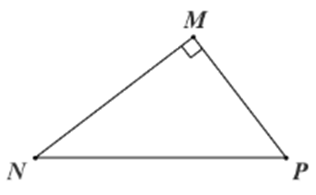
Vì tam giác \[MNP\] vuông tại \[M\] nên \[MN = NP.\cos N = 5.\frac{3}{5} = 3.\]
Vậy ta chọn phương án A.
Câu 5:
Cho hình vẽ dưới đây.
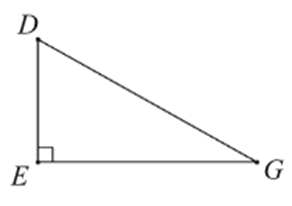
Hệ thức nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì tam giác \[DEG\] vuông tại \[E\] nên:
⦁ \[EG = DG.\sin D = DG.\cos G.\]
Suy ra \[DG = \frac{{EG}}{{\sin D}} = \frac{{EG}}{{\cos G}}.\] Do đó phương án A, C là khẳng định đúng.
⦁ \[DE = DG.\sin G.\] Suy ra \[DG = \frac{{DE}}{{\sin G}}.\] Do đó phương án B là khẳng định đúng.
⦁ \[EG = DE.\cot G.\] Suy ra \[DE = \frac{{EG}}{{\cot G}}.\] Do đó phương án D là khẳng định sai.
Vậy ta chọn phương án D.
Câu 6:
II. Thông hiểu
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 10{\rm{\;cm}},\,\,\widehat C = 30^\circ .\] Độ dài cạnh \[AB\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
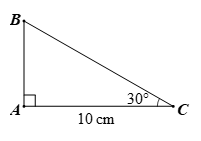
Vì tam giác \[ABC\] vuông tại \[A\] nên \[AB = AC.\tan C = 10.\tan 30^\circ = \frac{{10\sqrt 3 }}{3}\] (cm).
Do đó ta chọn phương án B.
Câu 7:
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 20{\rm{\;cm}},\,\,\widehat {C\,} = 60^\circ .\] Độ dài cạnh \[BC\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A

Vì tam giác \[ABC\] vuông tại \[A\] nên \[AC = BC.\cos C.\]
Suy ra \[BC = \frac{{AC}}{{\cos C}} = \frac{{20}}{{\cos 60^\circ }} = 40\] (cm).
Vậy ta chọn phương án A.
Câu 8:
Cho tam giác \[ABC\] vuông tại \[A\] có \[BC = 12{\rm{\;cm}},\,\,\widehat B = 40^\circ .\] Kết quả nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B

Vì tam giác \[ABC\] vuông tại \[A\] nên \[AC = BC.\sin B = 12.\sin 40^\circ \approx 7,71\] (cm).
Tam giác \[ABC\] vuông tại \[A\] nên \[\widehat B + \widehat C = 90^\circ \] (tổng hai góc nhọn của tam giác vuông).
Suy ra \[\widehat C = 90^\circ - \widehat B = 90^\circ - 40^\circ = 50^\circ .\]
Vậy ta chọn phương án B.
Câu 9:
Cho tam giác \[ABC\] vuông tại \[A\] có \[BC = 15{\rm{\;cm}},\,\,AB = 12{\rm{\;cm}}.\] Kết quả nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
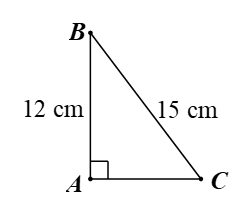
Xét tam giác \[ABC\] vuông tại \[A\], có: \[A{B^2} + A{C^2} = B{C^2}\] (Định lí Pythagore)
Suy ra \[A{C^2} = B{C^2} - A{B^2} = {15^2} - {12^2} = 81.\] Do đó \[AC = 9\] (cm).
Vì tam giác \[ABC\] vuông tại \[A\] nên \[\cos B = \frac{{AB}}{{BC}} = \frac{{12}}{{15}} = \frac{4}{5}.\]
Suy ra \[\widehat B \approx 36^\circ 52'.\]
Vậy ta chọn phương án C.
Câu 10:
Cho tam giác \[ABC\] vuông tại \[A\] có \[AB = 5{\rm{\;cm,}}\,\,AC = 7{\rm{\;cm}}{\rm{.}}\] Kết quả nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
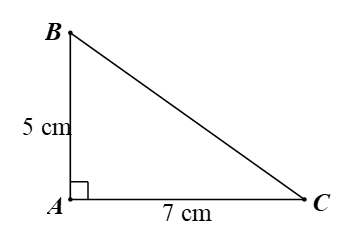
Xét tam giác \[ABC\] vuông tại \[A\], có: \[B{C^2} = A{B^2} + A{C^2}\] (Định lí Pythagore)
Suy ra \[B{C^2} = A{B^2} + A{C^2} = {5^2} + {7^2} = 74.\] Do đó \[BC = \sqrt {74} \] (cm).
Vì tam giác \[ABC\] vuông tại \[A\] nên \[\tan C = \frac{{AB}}{{AC}} = \frac{5}{7}.\]
Suy ra \[\widehat C \approx 35^\circ 32'.\]
Vậy ta chọn phương án A.
Câu 11:
Cho tam giác \[ABC\] vuông tại \[A\] có \[AB = 6{\rm{\;cm}},\,\,\tan B = \frac{5}{{12}}.\] Kết quả nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
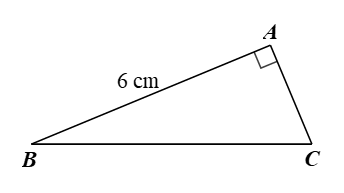
Xét tam giác \[ABC\] vuông tại \[A\], có:
⦁ \[AC = AB.\tan B = 6.\frac{5}{{12}} = \frac{5}{2} = 2,5\] (cm);
⦁ \[B{C^2} = A{B^2} + A{C^2} = {6^2} + {\left( {2,5} \right)^2} = 42,25\] (theo định lí Pythagore)
Suy ra \[BC = 6,5\] (cm).
Vậy ta chọn phương án D.
Câu 12:
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 16{\rm{\;cm}},\,\,\sin B = \frac{3}{5}.\] Kết quả nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C

Xét tam giác \[ABC\] vuông tại \[A\], có:
⦁ \(\widehat {B\,} + \widehat {C\,} = 90^\circ \) nên \[\cos C = \sin B = \frac{3}{5}.\] Do đó phương án A là khẳng định đúng.
⦁ \[\sin B = \frac{{AC}}{{BC}}.\] Suy ra \[BC = \frac{{AC}}{{\sin B}} = \frac{{16}}{{\frac{3}{5}}} = \frac{{80}}{3} \approx 26,7\] (cm). Do đó phương án C là khẳng định sai.
⦁ \[B{C^2} = A{B^2} + A{C^2}\] (theo định lí Pythagore)
Suy ra \[A{B^2} = B{C^2} - A{C^2} = {\left( {\frac{{80}}{3}} \right)^2} - {16^2} = \frac{{4096}}{9}.\] Do đó \[AB = \frac{{64}}{3} \approx 21,3\] (cm).
Như vậy phương án D là khẳng định đúng.
⦁ \(\cos B = \frac{{AB}}{{BC}} = \frac{{\frac{{64}}{3}}}{{\frac{{80}}{3}}} = \frac{4}{5}.\) Do đó phương án B là khẳng định đúng.
Vậy ta chọn phương án C.
Câu 13:
III. Vận dụng
Cho tam giác \[ABC\] nhọn có \[AB = 3,5;\,\,AC = 4;\,\,\widehat {A\,} = 40^\circ \] và \[BH\] là đường cao. Diện tích tam giác \[ABC\] gần nhất với
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
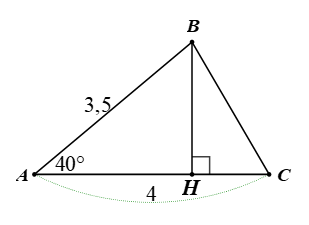
Vì tam giác \[ABC\] nhọn có \[BH\] là đường cao nên \[BH \bot AC.\]
Vì tam giác \[ABH\] vuông tại \[H\] nên \[BH = AB.\sin A = 3,5.\sin 40^\circ .\]
Diện tích tam giác \[ABC\] là: \[S = \frac{1}{2}.BH.AC = \frac{1}{2}.3,5.\sin 40^\circ .4 \approx 4,5\] (đvdt).
Vậy diện tích tam giác \[ABC\] khoảng \[4,5\] (đvdt).
Do đó ta chọn phương án B.
Câu 14:
Cho tam giác \[ABC\] có \[BC = 9{\rm{\;cm}},\,\,\widehat {ABC} = 50^\circ \] và \[\widehat {ACB} = 35^\circ .\] Gọi \[N\] là chân đường vuông góc hạ từ \[A\] xuống cạnh \[BC.\] Độ dài \[AN\] gần nhất với giá trị nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
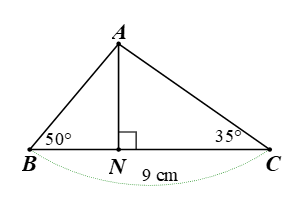
Tam giác \[ABC\] có \[AN\] là đường cao. Suy ra \[AN \bot BC\] tại \[N.\]
Vì tam giác \[ABN\] vuông tại \[N\] nên \[\tan B = \frac{{AN}}{{BN}}.\] Suy ra \[BN = \frac{{AN}}{{\tan B}}.\]
Tương tự, vì tam giác \[ACN\] vuông tại \[N\] nên \[\tan C = \frac{{AN}}{{CN}}.\] Suy ra \[CN = \frac{{AN}}{{\tan C}}.\]
Ta có \[BN + CN = BC = 9\] hay \[\frac{{AN}}{{\tan B}} + \frac{{AN}}{{\tan C}} = 9\]
Tức là, \[AN\left( {\frac{1}{{\tan 50^\circ }} + \frac{1}{{\tan 35^\circ }}} \right) = 9\]
Khi đó \[AN = 9:\left( {\frac{1}{{\tan 50^\circ }} + \frac{1}{{\tan 35^\circ }}} \right) \approx 3,97 \approx 4\] (cm).
Vậy độ dài \[AN\] gần nhất với giá trị là \[4\] cm.
Do đó ta chọn phương án C.
Câu 15:
Cho hình thang \[ABCD\] có \[\widehat {A\,} = \widehat {D\,} = 90^\circ ,\,\,\widehat {C\,} = 50^\circ .\] Biết rằng \[AB = 2;\,\,AD = 1,2.\] Khi đó diện tích hình thang \[ABCD\] gần nhất với
 Xem đáp án
Xem đáp án
Đáp án đúng là: C

Kẻ \[BH \bot CD\] tại \[H.\]
Ta có \[\widehat {BAD} = \widehat {ADH} = \widehat {BHD} = 90^\circ \] suy ra tứ giác \[ABHD\] là hình chữ nhật.
Do đó \[BH = AD = 1,2\] và \[DH = AB = 2.\]
Vì tam giác \[BCH\] vuông tại \[H\] nên \[\tan C = \frac{{BH}}{{CH}}.\]
Suy ra \[CH = \frac{{BH}}{{\tan C}} = \frac{{1,2}}{{\tan 50^\circ }} \approx 1.\]
Ta có \[CD = DH + HC \approx 2 + 1 \approx 3.\]
Diện tích hình thang \[ABCD\] là: \[S = \frac{1}{2}\left( {AB + CD} \right).AD \approx \frac{1}{2}.\left( {2 + 3} \right).1,2 \approx 3\] (đvdt).
Vậy ta chọn phương án C.
