Ôn thi Cấp tốc 789+ vào 10 môn Toán khu vực Khánh Hòa 2024 - 2025 (Đề 17)
-
65 lượt thi
-
5 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Không sử dụng máy tính cầm tay:
1) Rút gọn biểu thức \(A = \sqrt {36} + \sqrt 9 - \sqrt {81} \).
2) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{r}}{x + 3y = 6}\\{2x - 3y = 3}\end{array}} \right.\).
3) Giải phương trình \(3{x^2} - 7x + 4 = 0\).
 Xem đáp án
Xem đáp án
a) \(A = \sqrt {36} + \sqrt 9 - \sqrt {81} \)\( = \sqrt {{6^2}} + \sqrt {{3^2}} - \sqrt {{9^2}} \)\( = 6 + 3 - 9 = 0\).
Vậy \(A = 0\).
b) \(\left\{ {\begin{array}{*{20}{l}}{x + 3y = 6}\\{2x - 3y = 3}\end{array}} \right.\). Cộng từng vế của phương trình mới, ta được: \(3x = 9\), tức là \[x = 3.\]
Thế \[x = 3\] vào phương trình \(x + 3y = 6\) ta có: \(3 + 3y = 6\) nên \(3y = 3\) hay \[y = 1.\]
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x\,;\,\,y} \right) = \left( {3\,;\,\,1} \right).\)
c) \(3{x^2} - 7x + 4 = 0\).
Cách 1: Ta có \(a + b + c = 3 + \left( { - 7} \right) + 4 = 0\).
Do đó phương trình đã cho có hai nghiệm phân biệt: \(x = 1\,;\,\,x = \frac{c}{a} = \frac{4}{3}.\)
Cách 2: Ta có \(\Delta = {b^2} - 4ac = {\left( { - 7} \right)^2} - 4 \cdot 3 \cdot 4 = 1 > 0.\)
Do đó phương trình có hai nghiệm phân biệt:
\(x = \frac{{ - b + \sqrt {\rm{\Delta }} }}{{2a}} = \frac{{7 + \sqrt 1 }}{{2 \cdot 3}} = \frac{4}{3}\,;\,\,x = \frac{{ - b - \sqrt {\rm{\Delta }} }}{{2a}} = \frac{{7 - \sqrt 1 }}{{2 \cdot 3}} = 1.\)
Vậy phương trình có hai nghiệm phân biệt: \(x = 1\,;\,\,x = \frac{4}{3}.\)
Câu 2:
Trong mặt phẳng tọa độ \(Oxy\), cho parabol \(\left( P \right):y = 2{x^2}\) và đường thẳng \(\left( d \right):y = \left( {m + 1} \right)x + 4\), với \(m\) là tham số.
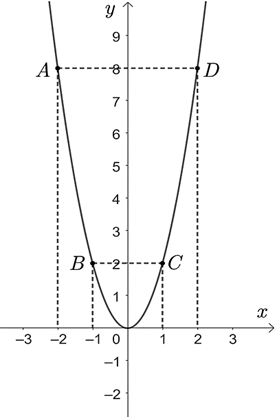
1) Vẽ parabol \(\left( P \right)\).
 Xem đáp án
Xem đáp án
1) Tập xác định \(D = \mathbb{R}\).
Bảng giá trị:
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = 2{x^2}\) |
8 |
2 |
0 |
2 |
8 |
2) Ta có: \({\rm{\Delta }} = {\left[ { - \left( {m + 1} \right)} \right]^2} - 4 \cdot 2 \cdot \left( { - 4} \right) = {\left( {m + 1} \right)^2} + 32 > 0\) với mọi \(m\) nên phương trình luôn có hai nghiệm phân biệt \({x_1},{x_2}\).
Theo Viète, ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{m + 1}}{2}}\\{{x_1} \cdot {x_2} = - 2}\end{array}} \right.\).
Thay vào biểu thức \({x_1} + {x_2} - {x_1} \cdot {x_2} = 6\) ta được: \(\frac{{m + 1}}{2} - \left( { - 2} \right) = 6\) hay \(\frac{{m + 1}}{2} = 4.\)
Do đó \(m + 1 = 8\) nên \(m = 7.\)
Vậy với \(m = 7\) thì \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1},{x_2}\) thỏa mãn \({x_1} + {x_2} - {x_1} \cdot {x_2} = 6\).
Câu 3:

Bán kính \(R\) là \(V = \frac{4}{3}\pi {R^3}\), thể tích hình trụ có bán kính đáy \(r\) và chiều cao \(h\) là \(V = \pi {r^2}h.\)
 Xem đáp án
Xem đáp án
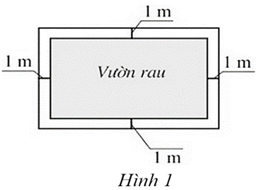
1) Gọi \(x,y\,\,\left( m \right)\) lần lượt là chiều dài và chiều rộng của mảnh đất đã cho \[\left( {x,y > 0\,;\,\,x > y} \right).\]
Nửa chu vi mảnh đất hình chữ nhật là: \(52:2 = 26\,\,\left( {\rm{m}} \right)\) hay \(x + y = 26. & \left( 1 \right)\)
Diện tích mảnh đất hình chữ nhật là: \(\left( {x - 2} \right)\left( {y - 2} \right) = 112\) hay \(xy - 2\left( {x + y} \right) = 108.\,\,\,\,\,\left( 2 \right)\)
Thay \[\left( 1 \right)\] vào \[\left( 2 \right)\] ta có \(xy - 2 \cdot 26 = 108\) nên \(xy = 160. & \left( 3 \right)\)
Từ \[\left( 1 \right)\] và \(\left( 3 \right)\) ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 26\\xy = 160\end{array} \right.\).
Từ phương trình thứ nhất ta có \(y = 26 - x\). Thế vào phương trình thứ hai, ta được
\(x\left( {26 - x} \right) = 160\) hay \({x^2} - 26x + 160 = 0 & \left( * \right)\)
Giải phương trình \(\left( * \right)\), ta được: \(x = 16\) hoặc \(x = 10\).
Với \(x = 16\) thì \(y = 26 - 16 = 10\) (thỏa mãn điều kiện \[x > y).\]
Với \(x = 10\) thì \(y = 26 - 10 = 16\) (không thỏa mãn điều kiện \[x > y).\]
Vậy chiều dài ban đầu của khu vườn là \(10\,\,{\rm{m}}\) và chiều rộng ban đầu của khu vườn là \(16\,\,{\rm{m}}{\rm{.}}\)
2) Thể tích của viên bi là: \({V_{bi}} = \frac{4}{3}\pi \cdot {3^3} = 36\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Phần thể tích nước tăng lên sau khi thả viên bi là:
\({V_t} = \pi {R^2}h = \pi \cdot {5^2} \cdot h = 25\pi h\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
Vì phần thể tích nước tăng bằng thể tích của viên bi nên \(25\pi h = 36\pi \), suy ra \(h = \frac{{36}}{{25}}\,\,\left( {{\rm{cm}}} \right).\)
Vậy sau khi thả viên bi vào thì mực nước trong ly dâng lên \(\frac{{36}}{{25}}\,\,{\rm{cm}}.\)
Câu 4:
Cho đường tròn \(\left( {O\,;\,\,R} \right)\) và điểm \(M\) nằm ngoài đường tròn (với \(OM \ne 2R).\) Qua \(M\) kẻ hai tiếp tuyến \(MA,\,\,MB\) đến đường tròn \(\left( O \right)\) (với \(A,B\) là các tiếp điểm).
1) Chứng minh tứ giác \(MAOB\) nội tiếp đường tròn.
2) Qua \(A\) kẻ đường thẳng song song với \(MB\) cắt đường tròn \(\left( O \right)\) tại \(C\) (khác \(A),\) đường thẳng \(MC\) cắt đường tròn \(\left( O \right)\) tại \(E\) (khác \(C).\) Chứng minh \(\widehat {AEB} = \widehat {BEM}\).
 Xem đáp án
Xem đáp án
1) Chứng minh tứ giác \(MAOB\) nội tiếp đường tròn.
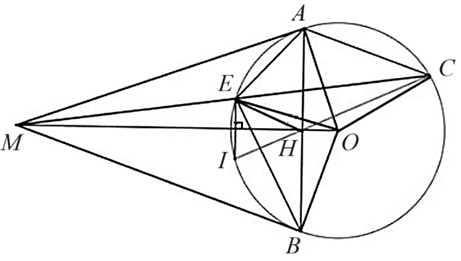
Vì \(MA,\,\,MB\) là tiếp tuyến của đường tròn \(\left( O \right)\) (với \(A,B\) là các tiếp điểm) nên
\(MA \bot OA\,,\,\,MB \bot OB\)
Hay \(\widehat {OAM} = \widehat {OBM} = 90^\circ \).
Xét tứ giác \(MAOB\) có
\(\widehat {OAM} + \widehat {OBM} = 90^\circ + 90^\circ = 180^\circ \).
Mà hai góc này ở vị trí đối diện nên tứ giác \(MAOB\) nội tiếp đường tròn.
2) Chứng minh \(\widehat {AEB} = \widehat {BEM}\).
Vì \(AC\,{\rm{//}}\,MB\,\,\left( {{\rm{gt}}} \right)\) nên \(\widehat {ACE} = \widehat {BME}\) (so le trong)
Mà \(\widehat {ACE} = \widehat {ABE}\) (góc nội tiếp cùng chắn cung \(AE)\), suy ra \(\widehat {ABE} = \widehat {BME}{\rm{.\;}}\)
Vì \(\Delta OBE\) cân tại \(O\) \(\left( {OB = OE} \right)\) nên \(\widehat {OBE} = \widehat {OEB}.\)
Suy ra \(\widehat {OBE} = \widehat {OEB} = \frac{{180^\circ - \widehat {BOE}}}{2} = 90^\circ - \frac{{\widehat {BOE}}}{2}.\)
Vì \[MB\] là tiếp tuyến với đường tròn \[\left( O \right)\] tại điểm \[B\] nên \(OB \bot MB\) hay \(\widehat {OBM} = 90^\circ .\)
Suy ra \[\widehat {MBE} = 90^\circ - \widehat {OBE}\]\[ = 90^\circ - \left( {90^\circ - \frac{{\widehat {BOE}}}{2}} \right) = \frac{{\widehat {BOE}}}{2}.\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\]
Mặt khác nên \[\widehat {BAE} = \frac{{\widehat {BOE}}}{2}.\,\,\,\,\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \(\widehat {BAE} = \widehat {MBE}\).
Xét \(\Delta ABE\) và \(\Delta BME\) có: \(ABE = BME\,\,\left( {{\rm{cmt}}} \right)\); \(\widehat {BAE} = \widehat {MBE}\,\,\left( {{\rm{cmt}}} \right)\).
Do đó . Suy ra \(\widehat {AEB} = \widehat {BEM}\) (hai góc tương ứng) (đpcm).
3) Chứng minh \(ME \cdot MC = MH \cdot MO\) và ba điểm \(C,\,\,H,\,\,I\) thẳng hàng.
Chứng minh \(ME \cdot MC = MH \cdot MO\).
Vì \(\Delta OAE\) cân tại \(O\) \(\left( {OA = OE} \right)\) nên \(\widehat {OAE} = \widehat {OEA}.\)
Suy ra \(\widehat {OAE} = \widehat {OEA} = \frac{{180^\circ - \widehat {AOE}}}{2} = 90^\circ - \frac{{\widehat {AOE}}}{2}.\)
Vì \[MA\] là tiếp tuyến với đường tròn \[\left( O \right)\] tại điểm \[A\] nên \(OA \bot MA\) hay \(\widehat {OAM} = 90^\circ .\)
Suy ra \[\widehat {MAE} = 90^\circ - \widehat {OAE}\]\[ = 90^\circ - \left( {90^\circ - \frac{{\widehat {AOE}}}{2}} \right) = \frac{{\widehat {AOE}}}{2}.\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\]
Mặt khác nên \[\widehat {ACM} = \frac{{\widehat {AOE}}}{2}.\,\,\,\,\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \(\widehat {MAE} = \widehat {ACM}\).
Xét \(\Delta AME\) và \(\Delta CMA\) có: \(\widehat {AME}\) chung; \(\widehat {MAE} = \widehat {ACM}\) (cmt)
Do đó . Suy ra \(\frac{{MA}}{{ME}} = \frac{{MC}}{{MA}}\) hay \(M{A^2} = ME \cdot MC.\,\,\,\,\,\left( 1 \right)\)
Vi \(MA,\,\,MB\) là hai tiếp tuyến của đường tròn \(\left( O \right)\) nên \(MA = MB.\)
Lại có \(OA = OB\) nên \(MO\) là đường trung trực của \(AB\) nên \(AB \bot MO\) tại \[H.\]
Xét \[\Delta OAM\] vuông tại \(A\) có đường cao \(AH\), ta có \(M{A^2} = MH \cdot MO.\,\,\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(ME \cdot MC = MH \cdot MO\) (đpcm).
Chứng minh ba điểm \(C,\,\,H,\,\,I\) thẳng hàng.
Do \(I\) lả điểm đối xứng của \(E\) qua \(OM\) nên \(OM\) là đường trung trực của \(EI\) nên \(OE = OI,\) suy ra \(I \in \left( {O\,;R} \right).\)
Do \(ME \cdot MC = MH \cdot MO\) nên \(\frac{{ME}}{{MH}} = \frac{{MO}}{{MC}}\).
Xét \(\Delta MEH\) và \(\Delta MOC\) có \(\widehat {OME}\) chung; \(\frac{{ME}}{{MH}} = \frac{{MO}}{{MC}}\) (cmt).
Do đó suy ra \(\widehat {MHE} = \widehat {MCO}\) (hai góc tương ứng).
Mà \(\widehat {MHE} + \widehat {EHO} = 180^\circ \) nên \(\widehat {MCO} + \widehat {EHO} = 180^\circ .\)
Mà \[\widehat {MCO}\] và \[\widehat {EHO}\] ở vị trí đối diện nên tứ giác \(EHOC\) nội tiếp đường tròn.
Suy ra \(\widehat {EHC} = \widehat {EOC}\) (cùng chắn cung \(EC\,).\)
Ta có \(\widehat {IHE} = 2\widehat {MHE}\) (tính chất đường trung trực)
Mà \(\widehat {MHE} = \widehat {MCO}\) nên
\(\widehat {IHE} + \widehat {EHC} = 2\widehat {MHE} + \widehat {EOC}\)\( = 2\widehat {MCO} + \widehat {EOC} = \widehat {MCO} + \widehat {CEO} + \widehat {EOC} = 180^\circ \).
Vậy ba điểm \(C,\,\,H,\,\,I\) thẳng hàng.
Câu 5:
Tủ sách học tốt của lớp 9A có hai loại tạp chí, gồm tạp chí Toán học & Tuổi trẻ (TH&TT) và tạp chí Pi. Biết rằng số tạp chí TH&TT nhiều hơn số tạp chí Pi; tổng số tạp chí TH&TT và hai lần số tạp chí Pi nhiều hơn 54; tổng số tạp chí Pi và hai lần số tạp chí TH&TT ít hơn 57. Tính số tạp chí mỗi loại.
 Xem đáp án
Xem đáp án
Gọi \(x\) là số tạp chí TH&TT; \(y\) là số tạp chí Pi \(\left( {x,\,\,y \in {\mathbb{N}^{\rm{*}}}} \right)\).
Theo đề bài ta có hệ bất phương trình sau:
\(\left\{ {\begin{array}{*{20}{l}}{x > y}\\{x + 2y > 54}\\{2x + y < 57}\end{array}} \right.\) nên \[\left\{ {\begin{array}{*{20}{l}}{x > y}\\{ - x + y > - 3}\end{array}} \right.\] hay \[\left\{ {\begin{array}{*{20}{l}}{x - y > 0}\\{x - y < 3}\end{array}} \right.\] suy ra \(0 < x - y < 3.\)
Vì \(x,\,\,y \in {\mathbb{N}^{\rm{*}}}\) nên \(x - y = 1\) hoặc \(x - y = 2.\)
Trường hợp 1: \(x - y = 1\) hay \(x = y + 1\).
Từ \(\left\{ {\begin{array}{*{20}{l}}{x + 2y > 54}\\{2x + y < 57}\end{array}} \right.\) hay \(\left\{ {\begin{array}{*{20}{l}}{y + 1 + 2y > 54}\\{2\left( {y + 1} \right) + y < 57}\end{array}} \right.\) nên \(\left\{ {\begin{array}{*{20}{l}}{y > \frac{{53}}{3}}\\{y < \frac{{55}}{3}}\end{array}} \right.\), suy ra \(\frac{{53}}{3} < y < \frac{{55}}{3}.\)
Do đó \(y = 18\) suy ra \(x = 19\).
Trường hợp 2: \(x - y = 2\) hay \(x = y + 2\)
Từ \(\left\{ {\begin{array}{*{20}{l}}{x + 2y > 54}\\{2x + y < 57}\end{array}} \right.\) hay \(\left\{ {\begin{array}{*{20}{l}}{y + 2 + 2y > 54}\\{2\left( {y + 2} \right) + y < 57}\end{array}} \right.\) nên \(\left\{ {\begin{array}{*{20}{l}}{y > 17}\\{y < \frac{{53}}{3}}\end{array}} \right.\) (không có số tự nhiên \(y\) thỏa mãn).
Vậy có 19 cuốn tạp chí TH&TT và 18 cuốn tạp chí Pi.
