Ôn thi Cấp tốc 789+ vào 10 môn Toán khu vực Nam Định 2024 - 2025 (Đề 14)
-
63 lượt thi
-
13 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 2:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 3:
Hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 5\\2x + y = - 5\end{array} \right.\) có nghiệm \(\left( {x;y} \right)\) là
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 4:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 6:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 7:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 8:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 9:
1) Chứng minh đẳng thức \(\frac{4}{{\sqrt 5 - \sqrt 3 }} - \sqrt {12} = 2\sqrt 5 .\)
2) Rút gọn biểu thức \(F = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x + 1}} + \frac{2}{{x - 1}}} \right)\) với \(x > 0\) và \(x \ne 1.\)
 Xem đáp án
Xem đáp án
1) Ta có: \(\frac{4}{{\sqrt 5 - \sqrt 3 }} - \sqrt {12} = \frac{{4\left( {\sqrt 5 + \sqrt 3 } \right)}}{{5 - 3}} - 2\sqrt 3 = \frac{{4\left( {\sqrt 5 + \sqrt 3 } \right)}}{2} - 2\sqrt 3 \)
\( = 2\sqrt 5 + 2\sqrt 5 - 2\sqrt 3 = 2\sqrt 5 .\)
Vậy đẳng thức được chứng minh.
2) Với \(x > 0\)và \(x \ne 1\), ta có:
\(F = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x + 1}} + \frac{2}{{x - 1}}} \right)\)
\[ = \left[ {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right]:\left[ {\frac{1}{{\sqrt x + 1}} + \frac{2}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right]\]
\[ = \frac{{x - 1}}{{\sqrt x \left( {\sqrt x - 1} \right)}}:\left[ {\frac{{\sqrt x - 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{2}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right]\]
\( = \frac{{x - 1}}{{\sqrt x \left( {\sqrt x - 1} \right)}}:\frac{{\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\)\( = \frac{{x - 1}}{{\sqrt x \left( {\sqrt x - 1} \right)}}:\frac{1}{{\sqrt x - 1}}\)
\( = \frac{{x - 1}}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\frac{{\sqrt x - 1}}{1}\)\( = \frac{{x - 1}}{{\sqrt x }}.\)
Vậy \(F = \frac{{x - 1}}{{\sqrt x }}\) với \(x > 0\) và \(x \ne 1.\)
Câu 10:
Cho phương trình \({x^2} - \left( {2m - 1} \right)x + {m^2} - 1 = 0\) (với \(m\) là tham số).
1) Giải phương trình với \(m = 1.\)
2) Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn:
\(\left( {{x_1} - 2{x_2}} \right)\left( {{x_2} - 2{x_1}} \right) = 9.\)
 Xem đáp án
Xem đáp án
1) Với \(m = 1,\) thay vào phương trình ta được:
\({x^2} - x = 0\) hay \(x\left( {x - 1} \right) = 0\) nên \(x = 0\) hoặc \(x = 1.\)
Vậy với \(m = 1\) thì phương trình có hai nghiệm là \(x = 0;\,\,x = 1.\)
2) Phương trình \({x^2} - \left( {2m - 1} \right)x + {m^2} - 1 = 0\) có:
\(\Delta = {\left[ { - \left( {2m - 1} \right)} \right]^2} - 4\left( {{m^2} - 1} \right) = 4{m^2} - 4m + 1 - 4{m^2} + 4 = - 4m + 5.\)
Để phương trình đã cho có hai nghiệm phân biệt thì \(\Delta > 0,\) tức là \( - 4m + 5 > 0\) hay \(m < \frac{5}{4}.\)
Như vậy, với \(m < \frac{5}{4}\) thì phương trình đã cho có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\)
Theo định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m - 1\\{x_1}{x_2} = {m^2} - 1.\end{array} \right.\)
Theo bài, \(\left( {{x_1} - 2{x_2}} \right)\left( {{x_2} - 2{x_1}} \right) = 9\)
\({x_1}{x_2} - 2x_1^2 - 2x_2^2 + 4{x_1}{x_2} = 9\)
\(5{x_1}{x_2} - 2\left( {x_1^2 + x_2^2} \right) = 9\)
\(9{x_1}{x_2} - 2\left( {x_1^2 + 2{x_1}{x_2} + x_2^2} \right) - 9 = 0\)
\(9{x_1}{x_2} - 2{\left( {{x_1} + {x_2}} \right)^2} - 9 = 0.\,\,\,\left( * \right)\)
Thay \[{x_1} + {x_2} = 2m - 1\] và \[{x_1}{x_2} = {m^2} - 1\] vào \(\left( * \right)\) ta được:
\(9\left( {{m^2} - 1} \right) - 2{\left( {2m - 1} \right)^2} - 9 = 0\)
\(9{m^2} - 9 - 2\left( {4{m^2} - 4m + 1} \right) - 9 = 0\)
\({m^2} + 8m - 20 = 0\)
\(m = 2\) hoặc \(m = - 10.\)
Ta thấy chỉ có giá trị \(m = - 10\) thỏa mãn \(m < \frac{5}{4}.\)
Vậy \(m = - 10.\)
Câu 11:
Giải hệ phương trình \(\left\{ \begin{array}{l}\sqrt {x - 5} + 3{\left( {y - 1} \right)^2} = 4\\2\sqrt {x - 5} + {y^2} - 2y = 2.\end{array} \right.\)
 Xem đáp án
Xem đáp án
Xét hệ phương trình: \(\left\{ \begin{array}{l}\sqrt {x - 5} + 3{\left( {y - 1} \right)^2} = 4\,\,\,\,\,\,\,\left( 1 \right)\\2\sqrt {x - 5} + {y^2} - 2y = 2\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Điều kiện xác định: \(x \ge 5.\)
Từ phương trình \(\left( 2 \right)\) ta có \(2\sqrt {x - 5} + {y^2} - 2y + 1 = 3\) hay \(2\sqrt {x - 5} + {\left( {y - 1} \right)^2} = 3.\,\,\,\left( 3 \right)\)
Do đó ta có hệ phương trình mới là: \(\left\{ \begin{array}{l}\sqrt {x - 5} + 3{\left( {y - 1} \right)^2} = 4\,\,\,\,\,\,\,\left( 1 \right)\\2\sqrt {x - 5} + {\left( {y - 1} \right)^2} = 3\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right.\)
Nhân cả hai vế của phương trình \(\left( 3 \right)\) với \(3,\) ta được hệ phương trình \(\left\{ \begin{array}{l}\sqrt {x - 5} + 3{\left( {y - 1} \right)^2} = 4\\6\sqrt {x - 5} + 3{\left( {y - 1} \right)^2} = 9.\end{array} \right.\)
Trừ từng vế phương trình thứ hai và phương trình thứ nhất của hệ trên, ta được:
\(5\sqrt {x - 5} = 5,\) suy ra \(\sqrt {x - 5} = 1,\) do đó \(x - 5 = 1\) nên \(x = 6\) (thỏa mãn \(x \ge 5).\)
Thay \(\sqrt {x - 5} = 1\) vào phương trình \(\left( 1 \right),\) ta được: \(1 + 3{\left( {y - 1} \right)^2} = 4,\) nên \({\left( {y - 1} \right)^2} = 1.\)
Do đó \(y - 1 = 1\) hoặc \(y - 1 = - 1\)
Suy ra \(y = 2\) hoặc \(y = 0.\)
Câu 12:
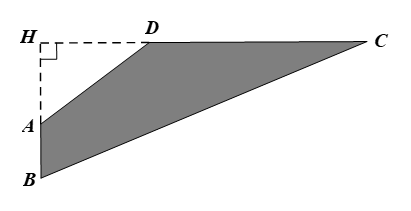
Tính diện tích của mảnh vườn (phần tô đậm).
2) Cho \(\Delta ABC\) nhọn nội tiếp đường tròn \(\left( O \right),\,\,AB < AC.\) Tiếp tuyến với \(\left( O \right)\) tại \(A\) cắt đường thẳng \(BC\) tại \(M.\) Gọi \(H\) là trung điểm của \(BC.\)
a) Chứng minh rằng các điểm \(A,\,\,O,\,\,H,\,\,M\) cùng nằm trên một đường tròn và \(M{A^2} = MB \cdot MC.\)
b) Từ điểm \(C\) kẻ đường thẳng song song với \(MO\) cắt đường kính \(AD\) của đường tròn \(\left( O \right)\) tại \[K.\] Chứng minh \(HK\) đi qua trung điểm của đoạn thẳng \(CD.\)
 Xem đáp án
Xem đáp án
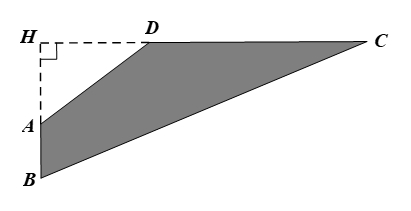
1) Tam giác \(BHC\) vuông tại \(H\) có:
\[BH = BC \cdot \sin \widehat {BCD} = 26 \cdot \frac{5}{{13}} = 10{\rm{\;(m)}}{\rm{.}}\]
Áp dụng định lí Pythagore cho tam giác này, ta được: \[B{C^2} = B{H^2} + H{C^2}\]
Suy ra \[H{C^2} = B{C^2}--B{H^2} = {26^2}--{10^2} = 576.\]
Do đó \(HC = \sqrt {576} = 24{\rm{\;(m)}}{\rm{.}}\)
Ta có: \(HA = BH - AB = 10 - 4 = 6{\rm{\;(m);}}\) \(HD = HC - CD = 24 - 16 = 8{\rm{\;(m)}}{\rm{.}}\)
Diện tích vườn là: \({S_{ABCD}} = {S_{\Delta HBC}} - {S_{\Delta HAD}} = \frac{1}{2} \cdot HB \cdot HC - \frac{1}{2} \cdot HA \cdot HD\)
\( = \frac{1}{2} \cdot 10 \cdot 24 - \frac{1}{2} \cdot 6 \cdot 8 = 120 - 24 = 96\) (m2).
2)
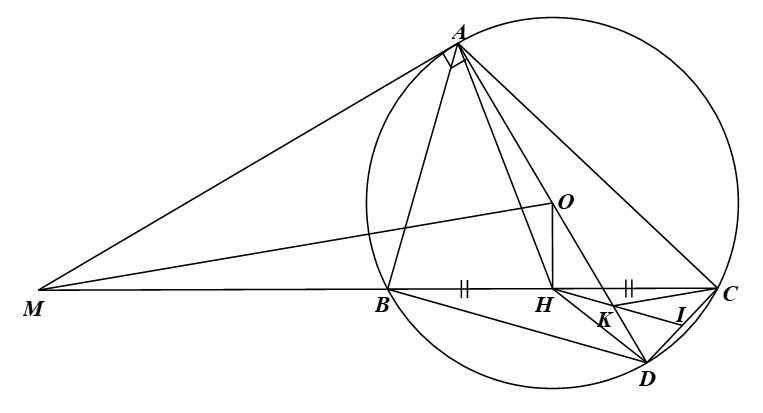
a) ⦁ Ta có: \(MA\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A\) nên \(OA \bot AM\) do đó \(\widehat {MAO} = 90^\circ .\)
Suy ra điểm \(A\) nằm trên đường tròn đường kính \(MO.\)
Ta có \(OB = OC\) nên \(O\) nằm trên đường trung trực của \(BC,\) lại có \(H\) là trung điểm của \(BC.\) Do đó \(OH\) là đường trung trực của \(BC\) nên \(OH \bot BC\) hay \(\widehat {MHO} = 90^\circ .\) Suy ra điểm \(H\) nằm trên đường tròn đường kính \(MO.\)
Như vậy, các điểm \(A,M,O,H\) cùng thuộc đường tròn đường kính \(MO.\)
⦁ Ta có \(\widehat {MAB} + \widehat {BAO} = 90^\circ \) suy ra \(\widehat {MAB} = 90^\circ - \widehat {BAO}.\,\,\,\left( 1 \right)\)
Xét \(\Delta OAB\) cân tại \(O\) (do \(OA = OB)\) nên \[\widehat {BAO} = \widehat {ABO} = \frac{{180^\circ - \widehat {AOB}}}{2} = 90^\circ - \frac{1}{2}\widehat {AOB}.\]
Xét đường tròn \(\left( O \right)\) có \(\widehat {ACB} = \frac{1}{2}\widehat {AOB}\) (góc nội tiếp và góc ở tâm cùng chắn cung \(AB)\)
Suy ra \[\widehat {BAO} = 90^\circ - \widehat {ACB}\] hay \[\widehat {ACB} = 90^\circ - \widehat {BAO}.\,\,\,\left( 2 \right)\]
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {MAB} = \widehat {ACB}.\)
Xét \(\Delta MAB\) và \(\Delta MCA\) có: \(\widehat {AMC}\) là góc chung và \(\widehat {MAB} = \widehat {MCA}\) (chứng minh trên)
Do đó (g.g), suy ra \(\frac{{MA}}{{MC}} = \frac{{MB}}{{MA}}\) hay \(M{A^2} = MB \cdot MC.\)
b)
• Giả sử \(\Delta ABC\) có đường tròn ngoại tiếp tâm \(O\) và đường kính \(AK\) nên tứ giác \(ABCK\) nội tiếp, suy ra \(\widehat {ACB} = \widehat {AKB}\) (hai góc nội tiếp cùng chắn cung \(AB).\)
Mà \(\widehat {ACB} = \widehat {ADB}\) (giả thiết) nên \(\widehat {ADB} = \widehat {AKB}.\) \(\left( 1 \right)\)
⦁ Gọi \(F\) là giao điểm của \(AK\) và \(BD,\) \(F\) nằm trong đường tròn \(\left( O \right).\)
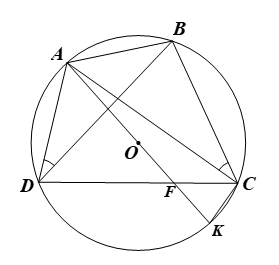
Xét \(\Delta AFD\) và \(\Delta BFK\) có: \(\widehat {AFD} = \widehat {BFK}\) (đối đỉnh) và \(\widehat {ADF} = \widehat {BKF}\) (chứng minh trên)
Do đó suy ra \(\frac{{AF}}{{BF}} = \frac{{DF}}{{KF}}\) nên \(\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}.\)
Xét \(\Delta DFK\) và \(\Delta AFB\) có: \(\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}\) và \[\widehat {DFK} = \widehat {AFB}\] (đối đỉnh)
Do đó suy ra \(\widehat {FDK} = \widehat {FAB}.\,\,\,\left( 2 \right)\)
⦁ Ta có \(\widehat {ABK}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ABK} = 90^\circ ,\) do đó \(\Delta ABK\) vuông tại \(B,\) suy ra \(\widehat {FAB} + \widehat {AKB} = 90^\circ .\,\,\,\left( 3 \right)\)
Từ \(\left( 1 \right),\,\,\left( 2 \right),\,\,\left( 3 \right)\) suy ra \(\widehat {ADB} + \widehat {FDK} = 90^\circ \) hay \(\widehat {ADK} = 90^\circ .\)
Khi đó \(\Delta ADK\) vuông tại \(D\) nên điểm \(D\) nằm trên đường tròn đường kính \(AK.\)
Suy ra tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AK.\)
Tứ giác \(AOHM\) nội tiếp nên \(\widehat {HAO} = \widehat {HMO}\) (hai góc nội tiếp cùng chắn cung \(HO)\)
Vì \[CK\,{\rm{//}}\,MO\] nên \[\widehat {KCM} = \widehat {OMC}\] (hai góc so le trong)
Do đó \[\widehat {KAH} = \widehat {KCH}.\] Từ bổ đề đã chứng minh ở trên, ta suy ra được tứ giác \[AHKC\] nội tiếp.
Suy ra \[\widehat {AKH} = \widehat {ACH}\] (hai góc nội tiếp cùng chắn cung \(AH)\)
Xét đường tròn \(\left( O \right)\) có \(\widehat {ACH} = \widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung \(AB)\)
Suy ra \(\widehat {AKH} = \widehat {ADB}.\) Mà hai góc này ở vị trí đồng vị nên \(HK\,{\rm{//}}\,BD.\)
Gọi \(I\) là giao điểm của \(HK\) và \(CD.\)
Xét \(\Delta BCD\) có \(H\) là trung điểm của \(BC\) và \(HI\,{\rm{//}}\,BD\) nên \(HI\) là đường trung bình của tam giác, do đó \(I\) là trung điểm của \(CD.\)
Vậy \(HK\) đi qua trung điểm của \(CD.\)
Câu 13:
1) Giải phương trình \(2\left( {{x^2} - 3x + 2} \right) = 3\sqrt {{x^3} + 8} .\)
2) Cho các số thực dương \(x,\,\,y\) thỏa mãn \(x + y \le 2.\) Tìm giá trị nhỏ nhất của biểu thức
\(P = \frac{3}{{{x^2} + {y^2}}} + \frac{{10}}{{xy}} + 8xy + 3.\)
 Xem đáp án
Xem đáp án
1) Điều kiện xác định:
\({x^3} + 8 \ge 0,\) hay \(\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right) \ge 0,\) nên \(x \ge - 2\) (do \({x^2} - 2x + 4 > 0\) với mọi \(x \in \mathbb{R}).\)
Ta có: \(2\left( {{x^2} - 3x + 2} \right) = 3\sqrt {{x^3} + 8} \)
\(2\left( {{x^2} - 2x + 4} \right) - 2\left( {x + 2} \right) = 3\sqrt {x + 2} \cdot \sqrt {{x^2} - 2x + 4} .\)
Đặt \(u = \sqrt {{x^2} - 2x + 4} \ge \sqrt 3 \) và \(v = \sqrt {x + 2} \ge 0.\)
Ta được phương trình: \(2{u^2} - 2{v^2} = 3uv\)
\(\left( {2u + v} \right)\left( {u - 2v} \right) = 0\)
\(u = 2v\) (vì \(u \ge \sqrt 3 ,v \ge 0\) nên \(2u + v > 0).\)
Suy ra \(\sqrt {{x^2} - 2x + 4} = 2\sqrt {x + 2} \)
\({x^2} - 2x + 4 = 4\left( {x + 2} \right)\)
\({x^2} - 6x - 4 = 0\)
\(x = 3 + \sqrt {13} \) hoặc \(x = 3 - \sqrt {13} .\)
Ta thấy các giá trị của \(x\) tìm được ở trên đều thỏa mãn điều kiện \(x \ge - 2.\)
Vậy phương trình có hai nghiệm là \(x = 3 + \sqrt {13} ;\,\,x = 3 - \sqrt {13} .\)
2) Ta có: \(P = \frac{3}{{{x^2} + {y^2}}} + \frac{{10}}{{xy}} + 8xy + 3.\)
Theo bất đẳng thức AM-GM, ta có: \[xy \le \frac{{{{\left( {x + y} \right)}^2}}}{4} = \frac{{{2^2}}}{4} = 1.\]
Chứng minh bổ đề: Với hai số thực dương \(a,\,\,b\) ta luôn có \(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}.\)
Theo bất đẳng thức Cauchy, ta có: \(a + b \ge 2\sqrt {ab} ;\,\,\frac{1}{a} + \frac{1}{b} \ge \frac{2}{{\sqrt {ab} }}.\)
Suy ra \(\left( {a + b} \right)\left( {\frac{1}{a} + \frac{1}{b}} \right) \ge 2\sqrt {ab} \cdot \frac{2}{{\sqrt {ab} }} = 4.\)
Do đó \(\left( {\frac{1}{a} + \frac{1}{b}} \right) \ge \frac{4}{{a + b}}.\)
Theo bổ đề trên, ta có:
\(P = \frac{3}{{{x^2} + {y^2}}} + \frac{{10}}{{xy}} + 8xy + 3 = \frac{3}{{{x^2} + {y^2}}} + \frac{3}{{2xy}} + 8xy + \frac{8}{{xy}} + \frac{1}{{2xy}} + 3\)
\( \ge \frac{{3 \cdot 4}}{{{x^2} + {y^2} + 2xy}} + 2 \cdot \sqrt {8xy \cdot \frac{8}{{xy}}} + \frac{1}{2} + 3 = \frac{{12}}{{{{\left( {x + y} \right)}^2}}} + 2 \cdot 8 + \frac{1}{2} + 3\)
\( \ge \frac{{12}}{{{2^2}}} + 16 + \frac{1}{2} + 3 = \frac{{45}}{2}.\)
Dấu bằng xảy ra khi và chỉ khi \(x = y = 1.\)
Vậy giá trị nhỏ nhất của \(P\) bằng \(\frac{{45}}{2}\) khi \(x = y = 1.\)
