Một hình trụ có bán kính đáy bằng \(3{\rm{\;cm}},\) chiều cao bằng \(4{\rm{\;cm}}.\) Diện tích xung quanh của hình trụ đó là: 

1) Chứng minh đẳng thức \(\frac{4}{{\sqrt 5  - \sqrt 3 }} - \sqrt {12}  = 2\sqrt 5 .\)

2) Rút gọn biểu thức \(F = \left( {\frac{{\sqrt x }}{{\sqrt x  - 1}} - \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x  + 1}} + \frac{2}{{x - 1}}} \right)\) với \(x > 0\) và \(x \ne 1.\)

Giải hệ phương trình \(\left\{ \begin{array}{l}\sqrt {x - 5} + 3{\left( {y - 1} \right)^2} = 4\\2\sqrt {x - 5} + {y^2} - 2y = 2.\end{array} \right.\)

1) Giải phương trình \(2\left( {{x^2} - 3x + 2} \right) = 3\sqrt {{x^3} + 8} .\)

2) Cho các số thực dương \(x,\,\,y\) thỏa mãn \(x + y \le 2.\) Tìm giá trị nhỏ nhất của biểu thức

\(P = \frac{3}{{{x^2} + {y^2}}} + \frac{{10}}{{xy}} + 8xy + 3.\)

Cho phương trình \({x^2} - \left( {2m - 1} \right)x + {m^2} - 1 = 0\) (với \(m\) là tham số).

1) Giải phương trình  với \(m = 1.\)

2) Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn:

\(\left( {{x_1} - 2{x_2}} \right)\left( {{x_2} - 2{x_1}} \right) = 9.\)

1) Mảnh vườn nhà ông An có hình dạng là tứ giác \(ABCD\) (như hình vẽ). Biết \(AB\) vuông góc với \(CD\) tại \(H;\) \(AB = 4{\rm{\;m;}}\) \(BC = 26{\rm{\;m}};\) \(CD = 16{\rm{\;m;}}\) \(\sin \widehat {BCD} = \frac{5}{{13}}.\)

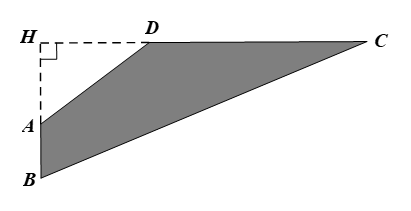
Tính diện tích của mảnh vườn (phần tô đậm).

2) Cho \(\Delta ABC\) nhọn nội tiếp đường tròn \(\left( O \right),\,\,AB < AC.\) Tiếp tuyến với \(\left( O \right)\) tại \(A\) cắt đường thẳng \(BC\) tại \(M.\) Gọi \(H\) là trung điểm của \(BC.\)

a) Chứng minh rằng các điểm \(A,\,\,O,\,\,H,\,\,M\) cùng nằm trên một đường tròn và \(M{A^2} = MB \cdot MC.\)

b) Từ điểm \(C\) kẻ đường thẳng song song với \(MO\) cắt đường kính \(AD\) của đường tròn \(\left( O \right)\) tại \[K.\] Chứng minh \(HK\) đi qua trung điểm của đoạn thẳng \(CD.\)