Trắc nghiệm Toán 9 Cánh diều Bài 3. Ứng dụng của tỉ số lượng giác của góc nhọn có đáp án
Trắc nghiệm Toán 9 Cánh diều Bài 3. Ứng dụng của tỉ số lượng giác của góc nhọn có đáp án
-
58 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I.Nhận biết
Giác kế là một dụng cụ dùng để
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
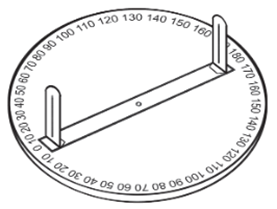
Giác kế là một loại dụng cụ dùng để đo góc.
Vậy ta chọn phương án B.
Câu 2:
Tại một thời điểm trong ngày, các tia nắng mặt trời tạo với phương ngang một góc bằng \[35^\circ ,\] khi đó cột \[AH\] có bóng trên mặt đất là đoạn \[BH\] dài \[10,4\] m.
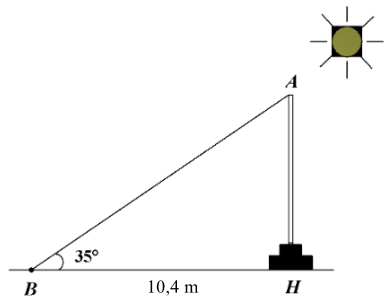
Trong các hệ thức sau, hệ thức nào là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì tam giác \[ABH\] vuông tại \[H\] nên \[AH = BH.\tan B = 10,4.\tan 35^\circ .\]
Vậy ta chọn phương án C.
Câu 3:
Một khúc sông rộng khoảng \[250\] m. Một con đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng \[320\] m mới sang được bờ bên kia. Giả sử dòng nước đã đẩy con đò đi lệch một góc \[\alpha \] (hình vẽ).
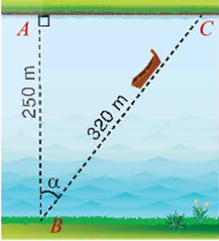
Khi đó để tính giá trị của \[\alpha \], cách đơn giản nhất là sử dụng tỉ số lượng giác nào của góc nhọn \[\alpha \]?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo đề bài, ta có độ dài cạnh góc vuông \[AB = 250\] (m) và độ dài cạnh huyền \[BC = 320\] (m).
Mà cạnh góc vuông \[AB\] là cạnh kề của góc nhọn \[\alpha \].
Do đó để tính giá trị của \[\alpha \], cách đơn giản nhất là ta nên sử dụng tỉ số giữa cạnh kề \[AB\] và cạnh huyền \[BC\] của góc nhọn \[\alpha \]. Tức là sử dụng côsin của góc nhọn \[\alpha \].
Vậy ta chọn phương án B.
Câu 4:
Một chiếc thang có chiều dài từ chân lên đến nấc thang cuối là \[5\] m được đặt vào thân cây cau (như hình vẽ).
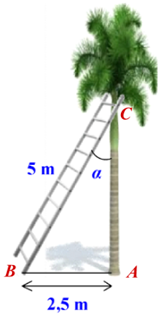
Người ta đo được khoảng cách từ chân thang đến gốc cây là \[2,5\] m. Khi đó để tính góc \[\alpha \] tạo bởi thang và thân cây cau, cách đơn giản nhất là sử dụng tỉ số lượng giác nào của góc nhọn \[\alpha \]?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Theo đề bài, ta có độ dài cạnh góc vuông \[AB = 2,5\] (m) và độ dài cạnh huyền \[BC = 5\] (m).
Mà cạnh góc vuông \[AB\] là cạnh đối của góc nhọn \[\alpha \].
Do đó để tính giá trị của \[\alpha \], cách đơn giản nhất là ta nên sử dụng tỉ số giữa cạnh đối \[AB\] và cạnh huyền \[BC\] của góc nhọn \[\alpha \]. Tức là sử dụng sin của góc nhọn \[\alpha \].
Vậy ta chọn phương án A.
Câu 5:
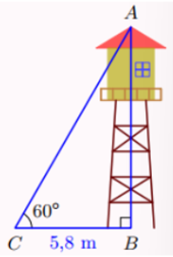
Chiều cao của tháp canh trong hình bên gần nhất với
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì tam giác \[ABC\] vuông tại \[B\] nên \[AB = BC.\tan C = BC.\tan 60^\circ = 5,8.\sqrt 3 \approx 10,05\] (m).
Do đó chiều cao của tháp canh khoảng \[10,05\] m.
Vậy ta chọn phương án C.
Câu 6:
II. Thông hiểu
Hình vẽ bên mô tả một chiếc thang có chiều dài \[AB = 7\] m được đặt dựa vào tường, khoảng cách từ chân thang đến chân tường là \[BH = 3\] m.
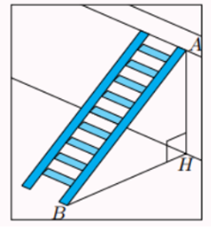
Góc tạo bởi cạnh \[AB\] và phần sàn nhà nằm ngang trên mặt đất gần nhất với
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Góc tạo bởi cạnh \[AB\] và phần sàn nhà nằm ngang trên mặt đất là \[\widehat {ABH}.\]
Ta có \[AB = 7\] m và \[BH = 3\] m.
Vì tam giác \[ABH\] vuông tại \[H\] nên \[\cos \widehat {ABH} = \frac{{BH}}{{AB}} = \frac{3}{7}.\]
Suy ra \[\widehat {ABH} \approx 65^\circ .\]
Do đó góc tạo bởi cạnh \[AB\] và phần sàn nhà nằm ngang trên mặt đất bằng khoảng \[65^\circ .\]
Vậy ta chọn phương án C.
Câu 7:
Tại một thời điểm trong ngày, các tia nắng mặt trời tạo với mặt đất một góc bằng \[55^\circ ,\] bóng của một cây xanh trên mặt đất dài \[14,25\] m (như hình vẽ).
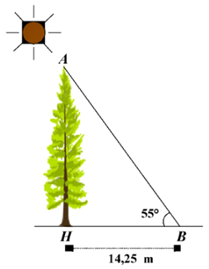
Chiều cao \[AH\] của cây xanh (làm tròn đến hàng phần trăm) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo đề, ta có \[BH = 14,25\] m và \[\widehat {ABH} = 55^\circ .\]
Vì tam giác \[ABH\] vuông tại H nên \[AH = BH.\tan \widehat {ABH} = 14,25.\tan 55^\circ \approx 20,35\] (m).
Do đó chiều cao của cây xanh là \[AH \approx 20,35\] m.
Vậy ta chọn phương án B.
Câu 8:
Một cái thang dài \[4,8\] m dựa vào tường và tạo với tường một góc \[32^\circ .\]
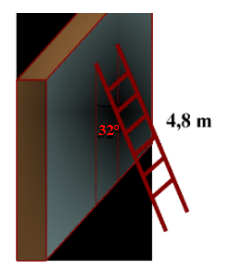
Chiều cao của thang so với mặt đất gần nhất với
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
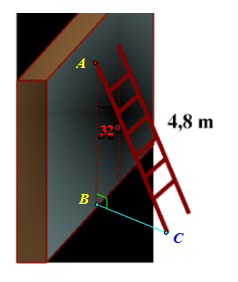
Theo đề, ta có \[AC = 4,8\] m và \[\widehat {BAC} = 32^\circ .\]
Chiều cao của thang so với mặt đất là độ dài \[AB.\]
Vì tam giác \[ABC\] vuông tại \[B\] nên \[AB = AC.\cos \widehat {BAC} = 4,8.\cos 32^\circ \approx 4,1\] (m).
Do đó chiều cao của thang so với mặt đất là \[4,1\] m.
Vậy ta chọn phương án D.
Câu 9:
Một cầu thủ sút bóng bị va vào mép xà ngang của cầu môn và bị bật ngược trở lại. Biết cầu môn cao \[2,4\] m và khoảng cách từ vị trí sút bóng đến chân cầu môn là \[25\] m.
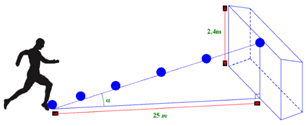
Góc \[\alpha \] tạo bởi đường đi của quả bóng và mặt đất gần nhất với
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
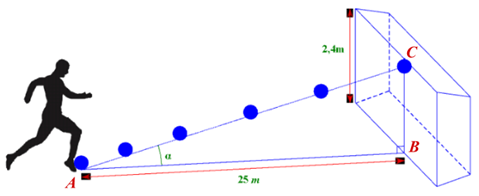
Vì cầu môn cao \[2,4\] m nên \[BC = 2,4\] m.
Vì khoảng cách từ vị trí sút bóng đến chân cầu môn là \[25\] m nên \[AB = 25\] m.
Do góc \[\alpha \] tạo bởi đường đi của quả bóng và mặt đất nên ta có \[\alpha = \widehat {BAC}.\]
Vì tam giác \[ABC\] vuông tại \[B\] nên \[\tan \alpha = \tan \widehat {BAC} = \frac{{BC}}{{AB}} = \frac{{2,4}}{{25}} = 0,096.\]
Suy ra \[\alpha \approx 5^\circ 29'.\]
Do đó góc tạo bởi đường đi của quả bóng và mặt đất là \[\alpha \approx 5^\circ 29'.\]
Vậy ta chọn phương án C.
Câu 10:
Một khúc sông rộng khoảng \[130\] m. Một con đò dự định chèo từ bờ bên này sang bờ bên kia theo phương vuông góc với bờ sông, nhưng do bị dòng nước đẩy xiên nên phải chèo khoảng \[150\] m mới sang được bờ bên kia (hình vẽ).
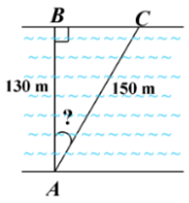
Khi đó dòng nước đã đẩy con đò đi lệch một góc khoảng bao nhiêu độ so với phương dự định ban đầu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có dòng nước đã đẩy con đò đi lệch một góc \[\widehat {BAC}\] so với dự định ban đầu.
Theo đề, ta có \[BA = 130\] (m) và \[AC = 150\] (m).
Vì tam giác \[ABC\] vuông tại \[B\] nên \[\cos \widehat {BAC} = \frac{{BA}}{{AC}} = \frac{{130}}{{150}} = \frac{{13}}{{15}}.\]
Suy ra \[\widehat {BAC} \approx 30^\circ .\]
Do đó dòng nước đã đẩy con đò đi lệch một góc \[30^\circ \] so với phương dự định ban đầu.
Vậy ta chọn phương án A.
Câu 11:
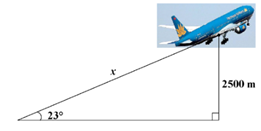
Một máy bay cất cánh theo phương hợp với mặt đất một góc \[23^\circ .\] Hỏi muốn đạt độ cao \[2\,\,500\] m thì máy bay phải bay một đoạn đường \[x\] dài khoảng bao nhiêu mét?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
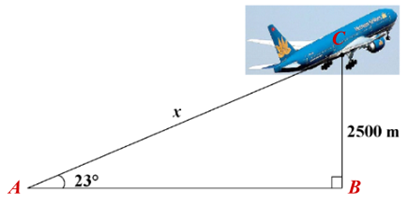
Theo đề, ta có \[\widehat {BAC} = 23^\circ \] và \[BC = 2\,\,500\] (m).
Vì tam giác \[ABC\] vuông tại \[B\] nên \[\sin \widehat {BAC} = \frac{{BC}}{{AC}}.\]
Suy ra \[AC = \frac{{BC}}{{\sin \widehat {BAC}}}\] hay \[x = \frac{{2\,\,500}}{{\sin 23^\circ }} \approx 6\,\,398\] (m).
Do đó muốn đạt độ cao \[2500\] m thì máy bay phải bay một đoạn đường \[x\] dài \[6\,\,398\] mét.
Vậy ta chọn phương án D.
Câu 12:
Một thanh chống dài \[2,5\] m hợp với tường một góc \[40^\circ \] để chống một tấm nhựa che nắng (hình vẽ).
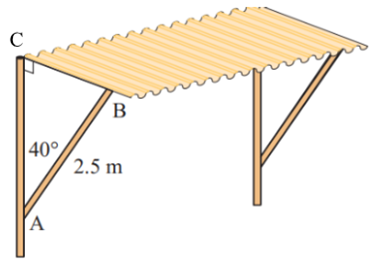
Hỏi khoảng cách từ tường đến vị trí đặt đầu thanh chống trên tấm nhựa là khoảng bao nhiêu mét?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Theo đề, ta có \[\widehat {BAC} = 40^\circ \] và \[AB = 2,5\] (m).
Vì tam giác \[ABC\] vuông tại \[C\] nên \[BC = AB.\sin \widehat {BAC} = 2,5.\sin 40^\circ \approx 1,6\] (m).
Do đó khoảng cách từ tường đến vị trí đặt đầu thanh chống trên tấm nhựa khoảng \[1,6\] mét.
Vậy ta chọn phương án A.
Câu 13:
III. Vận dụng
Hai bạn Việt và Nam cùng chơi thả diều trên một bãi đất phẳng, sợi dây diều của bạn Việt có độ dài \[100\] m và dây diều tạo với phương ngang một góc \[42^\circ ,\] còn sợi dây diều của bạn Nam có độ dài \[96\] m và dây diều tạo với phương ngang một góc \[45^\circ .\] Cho biết tầm mắt của cả hai bạn đều là \[1,55\] m và coi các dây diều được thả hết và căng thẳng (hình vẽ).
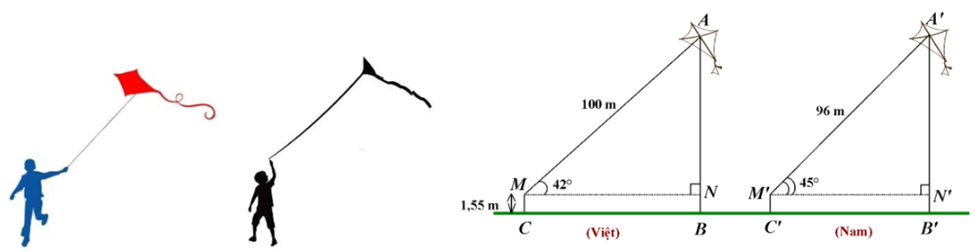
Trong các kết luận sau, kết luận nào đúng nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có \[NB = M'C' = N'B' = MC = 1,55\] (m).
Ta thấy độ cao của diều của bạn Việt và bạn Nam lần lượt là \[AB,\,\,A'B'.\]
Vì sợi dây diều của bạn Việt có độ dài \[100\] m nên ta có \[AM = 100\] (m).
Vì dây diều của bạn Việt tạo với phương ngang một góc \[42^\circ \] nên ta có \[\widehat {AMN} = 42^\circ .\]
Do tam giác \[AMN\] vuông tại \[N\] nên \[AN = AM.\sin \widehat {AMN} = 100.\sin 42^\circ \approx 66,91\] (m).
Thực hiện tương tự, ta được \[A'N' = 48\sqrt 2 \approx 67,88\] (m).
Độ cao của diều của bạn Việt là: \[AB = AN + NB \approx 66,91 + 1,55 = 68,46\] (m).
Độ cao của diều của bạn Nam là: \[A'B' = A'N' + N'B' \approx 67,88 + 1,55 = 69,43\] (m).
Vì \[69,43{\rm{\;m}} > 68,46{\rm{\;m}}\] nên \[A'B' > AB.\]
Mà \[A'B' - AB = 69,43 - 68,46 = 0,97\] (m).
Do đó so với mặt đất thì diều của bạn Nam lên cao hơn diều của bạn Việt và cao hơn \[0,97\] m.
Vậy ta chọn phương án B.
Câu 14:
Để thực hiện việc di chuyển của khách hàng giữa các tầng hàng trong siêu thị, người chủ đầu tư thường cho lắp hệ thống thang cuốn tự động. Biết rằng thang cuốn có góc nghiêng là \[35^\circ \] so với phương ngang và tốc độ truyền là \[0,65\] m/s, khoảng cách giữa hai tầng liên tiếp là \[4,2\] m.
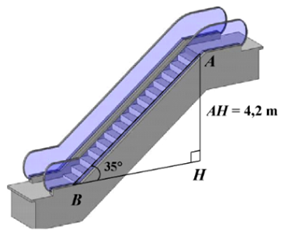
Hỏi một người khi bước vào thang cuốn và đứng yên thì cần khoảng bao nhiêu giây để có thể di chuyển từ tầng 1 lên tầng 2?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo đề, ta có: \[\widehat {ABH} = 35^\circ \] và \[AH = 4,2\] (m).
Vì tam giác \[ABH\] vuông tại \[H\] nên ta có \(AH = AB \cdot \sin \widehat {ABH}\).
Suy ra \[AB = \frac{{AH}}{{\sin \widehat {ABH}}} = \frac{{4,2}}{{\sin 35^\circ }}\] (m).
Thời gian để một người di chuyển từ tầng 1 lên tầng 2 là:
\[\frac{{4,2}}{{\sin 35^\circ }}:0,65 \approx 11,3\] (giây).
Vậy ta chọn phương án B.
Câu 15:
Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nhỏ giữa biển đến vị trí con sao biển \[C\] trên bãi cát (hình vẽ), người ta chọn một điểm \[B\] trên bãi biển cách điểm \[C\] một khoảng \[1{\rm{\;\;}}225\] m và dùng giác kế ngắm xác định được \[\widehat {ABC} = 75^\circ ;\,\,\widehat {ACB} = 65^\circ .\]

Khi đó khoảng cách \[AC\] khoảng bao nhiêu mét?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
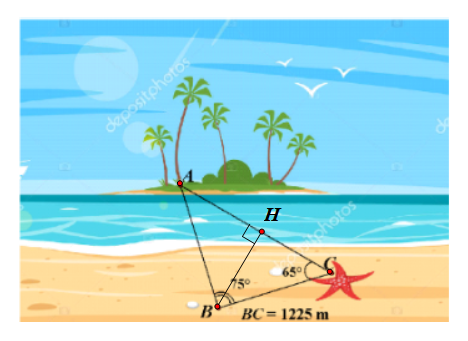
Kẻ \[BH \bot AC\] tại \[H.\]
Tam giác \[ABC,\] có: \[\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \] (định lí tổng ba góc của một tam giác)
Suy ra \[\widehat {BAC} = 180^\circ - \left( {\widehat {ABC} + \widehat {ACB}} \right) = 180^\circ - \left( {75^\circ + 65^\circ } \right) = 40^\circ .\]
Vì tam giác \[BCH\] vuông tại \[H\] nên:
⦁ \[BH = BC.\sin \widehat {BCH} = 1{\rm{\;\;}}225.\sin 65^\circ \] (m);
⦁ \[CH = BC.\cos \widehat {BCH} = 1{\rm{\;\;}}225.\cos 65^\circ \] (m).
Vì tam giác \[ABH\] vuông tại \[H\] nên \(BH = AH \cdot \tan \widehat {BAH}\)
Suy ra \[AH = \frac{{BH}}{{\tan \widehat {BAH}}} = \frac{{1{\rm{\;\;}}225 \cdot \sin 65^\circ }}{{\tan 40^\circ }}\] (m).
Khi đó \[AC = AH + CH = \frac{{1{\rm{\;\;}}225 \cdot \sin 65^\circ }}{{\tan 40^\circ }} + 1{\rm{\;\;}}225 \cdot \cos 65^\circ \approx 1{\rm{\;\;}}841\] (m).
Do đó khoảng cách \[AC\] khoảng \[1{\rm{\;\;}}841\] m.
Vậy ta chọn phương án B.
