15 câu trắc nghiệm Toán 9 Cánh diều Bài 3. Tần số ghép nhóm. Tần số tương đối ghép nhóm có đáp án
15 câu trắc nghiệm Toán 9 Cánh diều Bài 3. Tần số ghép nhóm. Tần số tương đối ghép nhóm có đáp án
-
42 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Nhóm số liệu \[\left[ {a;b} \right)\] là nhóm gồm các số liệu
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Nhóm số liệu \[\left[ {a;b} \right)\] là nhóm gồm các số liệu lớn hơn hoặc bằng \[a\] và nhỏ hơn \[b.\]
Do đó ta chọn phương án B.
Câu 2:
Biểu đồ tần số tương đối ghép nhóm dạng cột là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Biểu đồ tần số tương đối ghép nhóm dạng cột là biểu đồ gồm các cột liền nhau dùng để biểu diễn bảng tần số tương đối ghép nhóm.
Do đó ta chọn phương án D.
Câu 3:
Trục ngang của biểu đồ tần số tương đối ghép nhóm dạng cột xác định
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Trục ngang của biểu đồ tần số tương đối ghép nhóm dạng cột xác định các nhóm số liệu cần biểu diễn.
Do đó ta chọn phương án C.
Câu 4:
Bạn Hà ghi lại cự li nhảy xa của các bạn trong câu lạc bộ thể thao ở bảng tần số ghép nhóm sau (đơn vị: mét):
Cự li nhảy xa (mét) | \[\left[ {3,5;4} \right)\] | \[\left[ {4;4,5} \right)\] | \[\left[ {4,5;5} \right)\] | \[\left[ {5;5,5} \right)\] |
Tần số | 5 | 11 | 10 | 6 |
Trong bảng tần số ghép nhóm, có bao nhiêu nhóm số liệu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Quan sát bảng tần số ghép nhóm, ta thấy có 4 nhóm số liệu là: \[\left[ {3,5;4} \right),\,\,\left[ {4;4,5} \right),\,\,\left[ {4,5;5} \right),\,\,\left[ {5;5,5} \right).\]
Do đó ta chọn phương án A.
Câu 5:
Khối lượng (đơn vị: gam) của 32 củ khoai tây thu được được ghi lại trong bảng tần số tương đối ghép nhóm sau:
Khối lượng | \[\left[ {70;80} \right)\] | \[\left[ {80;90} \right)\] | \[\left[ {90;100} \right)\] | \[\left[ {100;110} \right)\] | \[\left[ {110;120} \right)\] |
Tần số tương đối | \[6,25\% \] | \[18,75\% \] | \[37,5\% \] | \[25\% \] | \[12,5\% \] |
Một củ khoai tây có khối lượng \[86\] gam. Vậy củ khoai tây đó nằm ở nhóm số liệu nào?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì \[86 \in \left[ {80;90} \right)\] nên củ khoai tây đó nằm ở nhóm số liệu \[\left[ {80;90} \right).\]
Vậy ta chọn phương án B.
Câu 6:
II. Thông hiểu
Trong một kỳ thi học sinh giỏi Toán (thang điểm 20) của một số học sinh, kết quả được cho bởi biểu đồ sau:
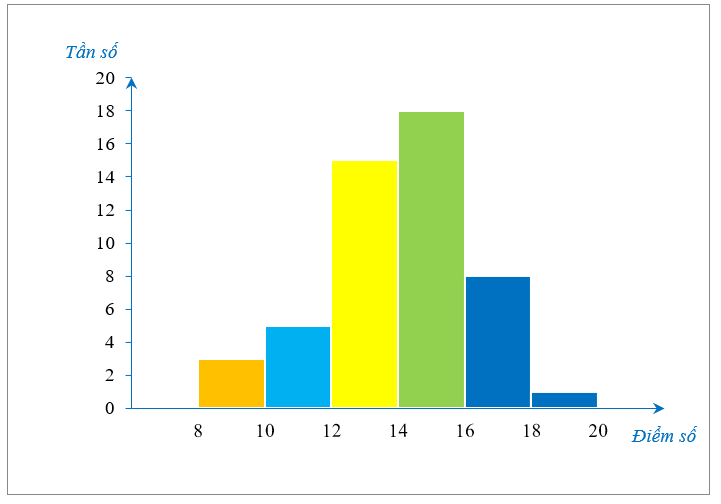
Có bao nhiêu học sinh tham gia kì thi học sinh giỏi Toán?
 Xem đáp án
Xem đáp án
Đáp án đúng: C
Số học sinh tham gia kì thi học sinh giỏi Toán là:
\(3 + 5 + 15 + 18 + 8 + 1 = 50\) (học sinh).
Câu 7:
Trong một kỳ thi học sinh giỏi Toán (thang điểm 20) của 50 học sinh, kết quả được cho bởi biểu đồ sau:
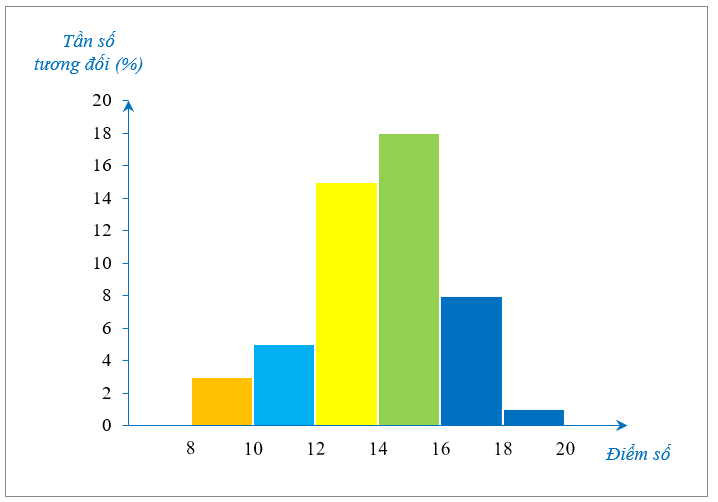
Tần số của nhóm thí sinh có điểm thi thấp nhất là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Quan sát biểu đồ, ta thấy nhóm thí sinh có điểm thi thấp nhất là \[\left[ {8;\,\,10} \right),\] có tần số là 3.
Do đó ta chọn phương án B.
Câu 8:
Một doanh nghiệp sản xuất xe ô tô khảo sát lượng xăng tiêu thụ trên \[100\] km của một số loại xe ô tô trên thị trường. Kết quả khảo sát được biểu diễn trong biểu đồ bên dưới:
![Một doanh nghiệp sản xuất xe ô tô khảo sát lượng xăng tiêu thụ trên \[100\] km của một số loại xe ô tô trên thị trường. Kết quả khảo sát được biểu diễn trong biểu đồ bên dưới:Tần số tương đối (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/11/blobid0-1731556252.png)
Tần số tương đối của số lượng xe ô tô tiêu thụ lượng xăng lớn hoặc hoặc bằng \(5\) và nhỏ hơn \(5,5\) là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Nhóm \(\left[ {5;\,\,5,5} \right)\) là nhóm biểu diễn số lượng xe ô tô tiêu thụ lượng xăng lớn hoặc hoặc bằng \(5\) và nhỏ hơn \(5,5\).
Quan sát biểu đồ, ta thấy tần số tương đối của nhóm \(\left[ {5;\,\,5,5} \right)\) là \(34\% .\)
Câu 9:
Cho biểu đồ tần số tương đối ghéo nhóm như hình vẽ sau biểu diễn tỉ lệ số lượng xe tiêu thụ xăng (lít) như sau:
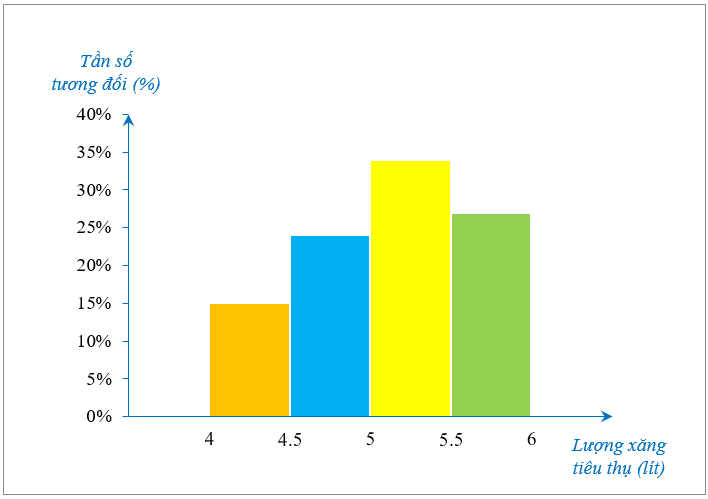
Trong \(300\) chiếc xe được khảo sát, có bao nhiêu chiếc xe tiêu thụ hết từ \(5\) đến dưới \(5,5\) lít xăng khi đi hết quãng đường \(100\) km?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Số xe tiêu thụ từ \(5\) đến dưới \(5,5\) lít xăng trong \(300\) chiếc xe được khảo sát là:
\(300 \cdot 34\% = 102\) (xe).
Câu 10:
Độ dài quãng đường (đơn vị: km) của một người đi bộ mỗi ngày trong tháng 8 được biểu diễn ở biểu đồ sau:
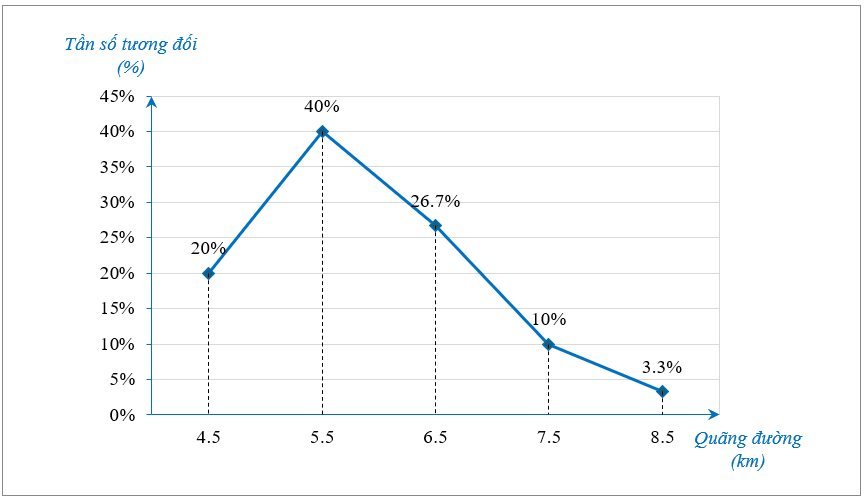
Biết rằng độ dài quãng đường của người đi bộ được chia thành các khoảng \[\left[ {4;\,\,5} \right),\,\,\left[ {5;\,\,6} \right),\,\,\left[ {6;\,\,7} \right),\,\,\left[ {7;\,\,8} \right),\,\,\left[ {8;\,\,9} \right).\] Tần số tương đối của các ngày có độ dài quãng đường thuộc nhóm \(\left[ {6;\,\,7} \right)\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Quan sát biểu đồ, ta thấy tần số tương đối của độ dài quãng đường thuộc nhóm \(\left[ {6;\,\,7} \right)\) là \[26,7\% .\]
Do đó ta chọn phương án B.
Câu 11:
Thời gian hoàn thành một bài kiểm tra trực tuyến của một số học sinh (đơn vị: phút) được biểu diễn ở biểu đồ sau:
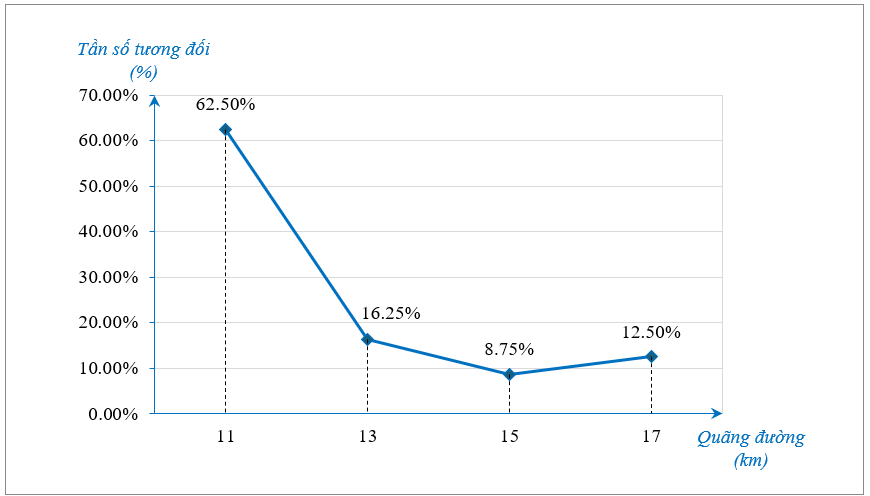
Biết rằng thời gian hoàn thành bài kiểm tra trực tuyến này được chia thành các khoảng \(\left[ {10;\,\,12} \right),\,\,\left[ {12;\,\,14} \right),\,\,\left[ {14;\,\,16} \right),\,\,\left[ {16;\,\,18} \right).\) Đa số học sinh hoàn thành bài kiểm tra trực tuyến trong khoảng thời gian nào?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Quan sát biểu đồ, ta thấy đa số học sinh hoàn thành bài kiểm tra trực tuyến trong khoảng thời gian từ 10 đến dưới 12 phút (chiếm tỉ lệ \[62,5\% ).\]
Do đó ta chọn phương án A.
Câu 12:
Người ta tiến hành phỏng vấn \(40\) người về một mẫu sản phẩm mới. Người điều tra yêu cầu mỗi người được phỏng vấn cho điểm mẫu sản phẩm đó theo thang điểm là \(100\). Kết quả thống kê là như sau:
50 | 60 | 62 | 64 | 71 | 73 | 70 | 70 | 70 | 75 |
75 | 52 | 55 | 69 | 80 | 75 | 75 | 78 | 79 | 73 |
55 | 72 | 71 | 85 | 82 | 90 | 78 | 78 | 75 | 75 |
65 | 85 | 87 | 77 | 81 | 79 | 99 | 75 | 70 | 72 |
Ghép các số liệu thành năm nhóm như sau: \(\left[ {50;60} \right)\); \(\left[ {60;70} \right)\); \(\left[ {70;80} \right)\); \(\left[ {80;90} \right)\); \(\left[ {90;100} \right)\).
Tần số tương đối ghép nhóm của nhóm \(\left[ {50;60} \right)\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tần số ghép nhóm của nhóm \(\left[ {50;60} \right)\) là \(4\).
Tần số tương đối ghép nhóm của nhóm \(\left[ {50;60} \right)\) là \(\frac{4}{{40}} \cdot 100\% = 10\% .\)
Câu 13:
III. Vận dụng
Bảng sau ghi lại thời gian một bác sĩ khám cho một số bệnh nhân (đơn vị: phút):
|
Thời gian |
\[\left[ {5;6,5} \right)\] |
\[\left[ {6,5;8} \right)\] |
\[\left[ {8;9,5} \right)\] |
\[\left[ {9,5;11} \right)\] |
\[\left[ {11;12,5} \right)\] |
|
Tần số |
6 |
6 |
4 |
1 |
3 |
Thời gian bác sĩ khám cho bệnh nhân chủ yếu là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Quan sát bảng tần số ghép nhóm, ta thấy thời gian bác sĩ khám cho bệnh nhân chủ yếu trong khoảng từ 5 đến dưới 6,5 phút (với tần số là 6 bệnh nhân) hoặc từ 6,5 đến dưới 8 phút (với tần số là 6 bệnh nhân).
Do đó ta chọn phương án C.
Câu 14:
Điểm thi giữa kì môn Tiếng Anh lớp 9A biểu diễn bởi biểu đồ sau
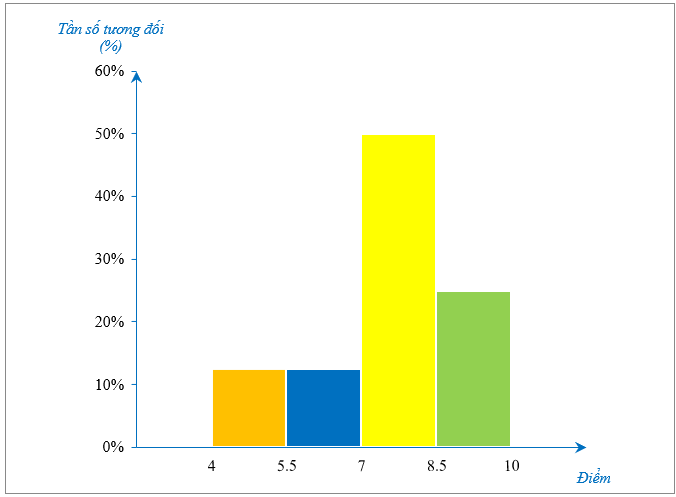
Biết rằng số học sinh có điểm thuộc nhóm \[\left[ {5,5;7} \right)\] là 5 học sinh. Tổng số học sinh lớp 9A là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi \[n\] là số học sinh của lớp 9A.
Theo đề, ta có số học sinh có điểm thuộc nhóm \[\left[ {5,5;7} \right)\] là 5 học sinh. Suy ra \[{m_2} = 5.\]
Quan sát biểu đồ, ta thấy nhóm \[\left[ {5,5;7} \right)\] có tần số tương đối là \[12,5\% .\]
Tức là, \[{f_2} = 12,5\% .\]
Do đó \[n = 5:12,5\% = 40.\]
Vậy lớp 9A có tất cả 40 học sinh, ta chọn phương án B.
Câu 15:
Một thư viện thống kê số lượng người đến đọc sách mỗi ngày trong 200 ngày liên tiếp. Sau khi ghép nhóm mẫu số liệu thu được, người ta nhận được biểu đồ sau:
![Một thư viện thống kê số lượng người đến đọc sách mỗi ngày trong 200 ngày liên tiếp. Sau khi ghép nhóm mẫu số liệu thu được, người ta nhận được biểu đồ sau:Biết có \[400\] người đã đến đọc sá (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/11/blobid0-1731556520.png)
Biết có \[400\] người đã đến đọc sách trong các ngày được khảo sát, khi đó nhóm \[\left[ {60;80} \right)\] nhiều hơn nhóm \[\left[ {40;60} \right)\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Theo đề, ta thấy có \[400\] người đã đến đọc sách trong các ngày được khảo sát.
Suy ra \[n = 400.\]
⦁ Nhóm \[\left[ {60;80} \right)\] có giá trị đại diện là \(70,\) từ biểu đồ ta thấy giá trị này có tần số tương đối ghép nhóm là \[35\% .\]
Suy ra tần số ghép nhóm của nhóm \[\left[ {60;80} \right)\] là: \[{m_4} = 400 \cdot 35\% = 140.\]
⦁ Nhóm \[\left[ {40;60} \right)\] có giá trị đại diện là \(50,\) từ biểu đồ ta thấy giá trị này có tần số tương đối ghép nhóm là \[30\% .\]
Suy ra tần số ghép nhóm của nhóm \[\left[ {40;60} \right)\] là: \[{m_3} = 400 \cdot 30\% = 120.\]
Do đó nhóm \[\left[ {60;80} \right)\] nhiều hơn nhóm \[\left[ {40;60} \right)\] là \[140 - 120 = 20\] người.
Vậy ta chọn phương án A.
